Surface Area of a Triangular Prism Formula
A prism that has 3 rectangular faces and 2 parallel triangular bases, then it is a triangular prism. This three-sided prism is a polyhedron that has a rectangular base, a translated copy and 3 faces joining sides.
The surface area of a triangular prism is nothing but the amount of space on the outside. This formula will show what is the surface area of the triangular prism. For finding that out we need the height, side and base length.
This is how a Triangular prism looks like:
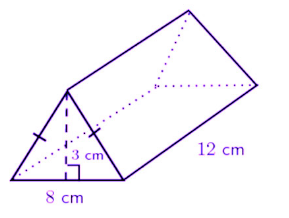
The Surface area of a triangular prism is given as: \[\large ab+3bh\]
Solved example
Example: Calculate the surface area of a triangular prism with side 7 cm, base 5 cm and height 6 cm.
Solution
We know that Surface area of a triangular prism is:
Given,
a = 7
b = 5
h = 6
Using the formula:
So, the surface area of the given triangular prism is
Comments