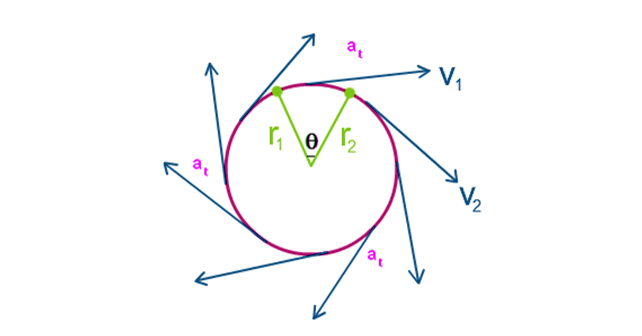
The concept of tangential acceleration is used to measure the change in the tangential velocity of a point with a specific radius with the change in time. The linear and tangential accelerations are the same but in the tangential direction, which leads to the circular motion. Tangential acceleration is defined as the rate of change of tangential velocity of the matter in the circular path.
Tangential Acceleration Formula
\(\begin{array}{l}a_{t}=\frac{\Delta v}{\Delta t}\end{array} \) |
Formula for Tangential Acceleration In Terms Of Distance
\(\begin{array}{l}a_{t}=\frac{\mathrm{d}^{2} s}{\mathrm{d} t^{2}}\end{array} \)
Or\(\begin{array}{l}a_{t}=v.\frac{dv}{ds}\end{array} \) |
Notations Used In The Formula
- at is the tangential acceleration
- Δv is the change in the angular velocity
- Δt is the change in time
- v is the linear velocity
- s is the distance covered
- t is the time taken
The formula of tangential acceleration is used to calculate the tangential acceleration and related parameters and the unit is m/s2
Linear Acceleration Formula
Linear acceleration is defined as the uniform acceleration caused by a moving body in a straight line. There are three equations that are important in linear acceleration depending upon the parameters like initial and final velocity, displacement, time and acceleration.
Following is the table explain all the three equations that are used in linear acceleration:
| First equation of motion | v=u+at |
| Second equation of motion | \(\begin{array}{l}s=ut+\frac{1}{2}at^{2}\end{array} \) |
| The third equation of motion | \(\begin{array}{l}v^{2}=u^{2}+2as\end{array} \) |
Notations Used In The Formula
- u is the initial velocity
- a is the acceleration
- t is the time taken
- v is the final velocity
- s is the acceleration
Solved Example
Example 1:
With a speed of 20 m / s to 80 m/s in 30s, a body accelerates uniformly on a circular path. Calculate the acceleration to tangential.
Solution:
Given parameters
vi = 20 m/s
vf = 80 m/s
dv = vf – vi = 80 – 20 = 60 m/s
dt = tf – ti = 30 – 0 = 30sec
The formula of tangential acceleration is
at = dv / dt
at = 60 / 30
at = 2 m/s2
Stay tuned with BYJU’S to learn more on Physics-related concepts.
Comments