The Distance Formula
In analytic geometry, the distance between two points of the xy-plane can be found using the distance formula. Distance Formula is used to calculate the distance between two points. The distance between (x1, y1) and (x2, y2) is given by: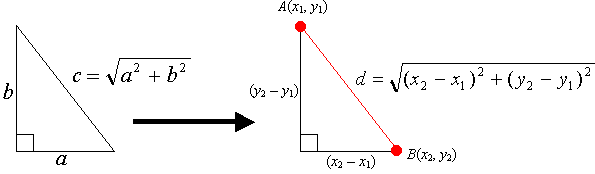
\[\large d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\]
Example For The Distance Formula
Question: Given the points (-1, -2) and (-3, 5), find the distance between them.
Solution:
Label the points as follows
\(\begin{array}{l}\left(x_{1},y_{1}\right)=\left(-1, -2\right) and \left(x_{2},y_{2}\right)=\left(-3, 5\right)\end{array} \)
Therefore:
\(\begin{array}{l}x_{1}=-1,\: y_{1}=-2,\: x_{2}=-3, and\: y_{2}=5\end{array} \)
To find the distance (d) between the points, use the distance formula:
\(\begin{array}{l}d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{\left(-3-\left(-1\right)\right)^{2}+\left(5-\left(-2\right)\right)^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{\left(-3+1\right)^{2}+\left(5+2\right)^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{\left(-2\right)^{2}+\left(7\right)^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{4+49}\end{array} \)
\(\begin{array}{l}=\sqrt{53}\end{array} \)

Comments