The motion of objects soaring through the air has been a source of fascination for scientists and curious individuals throughout history. In physics, projectile motion is a fundamental concept that unveils the captivating nature of objects propelled into the air, guided solely by the force of gravity. This article explores projectile motion, unravelling its core principles, delving into its mathematical formulations and shedding light on its practical applications in the real world.
| Table of Contents: |
What Is Projectile?
A projectile is any object thrown into space upon which the only acting force is gravity. The primary force acting on a projectile is gravity. This doesn’t necessarily mean that other forces do not act on it, just that their effect is minimal compared to gravity. The path followed by a projectile is known as a trajectory. A baseball batted or thrown is an example of a projectile.
What Is Projectile Motion?
When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration directed towards the centre of the earth (we assume that the particle remains close to the earth’s surface). The path of such a particle is called a projectile, and the motion is called projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
- Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle.
- Along the y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle.
Acceleration in the horizontal projectile motion and vertical projectile motion of a particle: When a particle is projected in the air with some speed, the only force acting on it during its time in the air is the acceleration due to gravity (g). This acceleration acts vertically downward. There is no acceleration in the horizontal direction, which means that the velocity of the particle in the horizontal direction remains constant.
Parabolic Motion of Projectiles
Let us consider a ball projected at an angle θ with respect to the horizontal x-axis with the initial velocity u as shown below:
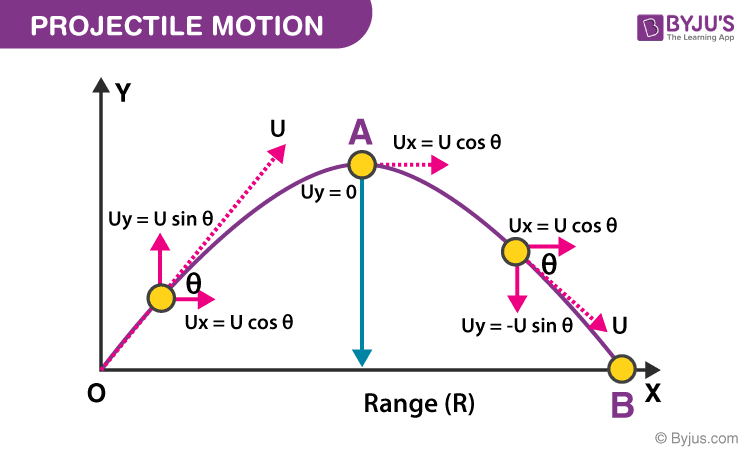
The point O is called the point of projection; θ is the angle of projection and OB = Horizontal Range or Simply Range. The total time taken by the particle from reaching O to B is called the time of flight.
For finding different parameters related to projectile motion, we can make use of differential equations of motions:

Watch the video and practice projectile motion problems

Total Time of Flight
Resultant displacement (s) = 0 in Vertical direction. Therefore, the time of flight formula is given by using the Equation of motion:
gt2 = 2(uyt – sy) [Here, uy = u sin θ and sy = 0]
i.e. gt2 = 2t × u sin θ
Therefore, the time of flight formula (t) is given by:
\(\begin{array}{l}Total\,Time\,of\,Flight\,(t)=\frac{2u\sin\Theta}{g}\end{array} \)
Horizontal Range
Horizontal Range (OA) = Horizontal component of velocity (ux) × Total Flight Time (t)
R = u cos θ × 2u×sinθg
Therefore, in a projectile motion, the Horizontal Range is given by (R):
\(\begin{array}{l}Horizontal\,Range\,(R)=\frac{u^2\sin 2\Theta }{g}\end{array} \)
Maximum Height of Projectile
After understanding what a projectile is, let us know the maximum height of the projectile. The object’s maximum height is the highest vertical position along its trajectory. The horizontal displacement of the projectile is called the range of the projectile. The range of the projectile depends on the object’s initial velocity.
If v is the initial velocity, g = acceleration due to gravity and H = maximum height in metres, θ = angle of the initial velocity from the horizontal plane (radians or degrees).
The maximum height of the projectile is given by the formula:
\(\begin{array}{l}H=\frac{v_{0}^{2}sin^{2}\theta}{2g}\end{array} \)
The Equation of Trajectory
\(\begin{array}{l}Equation\,of\,Trajectory = x\tan \Theta -\frac{gx^2}{2u^2cos^{2}\Theta }\end{array} \)
This is the equation of trajectory in projectile motion, and it proves that the projectile motion is always parabolic in nature.
Watch the video and learn about 2D motion and projectile motion

Basketball Physics
We know that projectile motion is a type of two-dimensional motion or motion in a plane. It is assumed that the only force acting on a projectile (the object experiencing projectile motion) is the force due to gravity. But how can we define projectile motion in the real world? How are the concepts of projectile motion applicable to daily life? Let us see some real-life examples of projectile motion in two dimensions.
All of us know about basketball. The player jumps a little to score a basket and throws the ball in the basket. The motion of the ball is in the form of a projectile. Hence, it is referred to as projectile motion. What advantage does jumping give to their chances of scoring a basket? Now, apart from basketballs, if we throw a cricket ball, a stone in a river, a javelin throw, an angry bird, a football or a bullet, all these motions have one thing in common. They all show a projectile motion. And that is, the moment they are released, there is only one force acting on them- gravity. It pulls them downwards, thus giving all of them an equal, impartial acceleration.
It implies that if something is being thrown in the air, it can easily be predicted how long the projectile will be in the air and at what distance it will hit the ground from the initial point. If the air resistance is neglected, there would be no acceleration in the horizontal direction. This implies that as long as a body is thrown near the surface, the body’s motion can be considered a two-dimensional motion, with acceleration only in one direction. But how can it be concluded that a body thrown in the air follows a two-dimensional path? To understand this, let us assume a ball that is rolling as shown below:



Thus, it can be concluded that the minimum number of coordinates required to define the motion of a body completely determines the dimension of its motion.
Watch the video and learn about projectile motion on inclined plane

Solved Examples
An object is launched at a velocity of 40 m/s in a direction making an angle of 50° upward with the horizontal.
Q1. What is the maximum height reached by the object?
Q2. What is the object’s total flight time (between launch and touching the ground)?
Q3. What is the object’s horizontal range (maximum x above ground)?
Solution:
The velocity components Vx and Vy are given by the formula:

In the given problem,
The component y gives the height of the projectile, and it reaches its maximum value when the component Vy is equal to zero. That is when the projectile changes from moving upward to moving downward.
Substituting and solving for t, we get
To find the maximum height, substitute t in the equation y, and we get
Solving, we get
The maximum height reached by the object is 47.9 metres.
The time of flight is the interval between when the projectile is launched (t1) and when the projectile touches the ground (t2).
Hence,
Solve for t
Solving, we get two solutions as follows:
Time of flight can be calculated as follows:
Horizontal Range is the horizontal distance given by x at t = t2.
Projectile Motion | Kickstart Series

Half Projectile Motion

Time of Flight in 1D motion

Projectile Motion in an Inclined Plane

Frequently Asked Questions – FAQs
What is a projectile?
What is a trajectory?
Define time of flight.
Give the time of flight formula?
State true or false: the minimum number of coordinates required to completely define the motion of a body determines the dimension of its motion.
Hope you learned projectile motion, time of flight formula, horizontal range, maximum height, and the equation of trajectory. Stay tuned with BYJU’S to learn more about projectile motion and its applications.


Nice explanation
great notes
helped me a lot!!!!!!!!
great thanks!for your help
wow information. thanks for it
very helpful
Thnku for giving this . It helped me a lot.
thank you very much! It’s very helpful
Thanks so much, helpful it is.
thanks u so much God u
Nice explanation
Thank u
Helped me indeed
helpful
This explanation is super useful,thanks for this.
much helpful very good
helped me so much while doing the notes, thankyou so much byju’s learning.
Wow
Great notes
It is a very nice note
Thank you so much it helped me a lot
It was helpful 😌😌😌😌
👌👌
Very helpful!! Thanks