How to Prepare for CAT Exam 2023 – The candidates who are interested to appear in the upcoming exam might be confused by thinking about how they start CAT preparation. This is one of the most common questions as everyone wants to crack CAT to get admission in the top-most B-schools in India. Please refer BYJU’S CAT College Predictor tool.
The CAT exam is a highly competitive exam, which is conducted by one of the IIMs on a rotational basis. Each year, thousands of fresh graduates and experienced professionals take the exam from various fields.
Ultimate Guide to Kickstart your CAT Exam Preparation
Download the e-book now
Thus, it is crucial for aspiring candidates to be well prepared for the exam to get into their preferred B-school. For in-depth CAT preparation, it is always necessary to create a systematic study strategy and to have an experienced faculty to guide you along.
In this article:
- CAT Preparation Study Material
- Tips on How to Prepare for CAT Exam
- Best Online Videos for CAT Preparations
- Explore about CAT Preparation with BYJU’S
- FAQs on CAT Preparation
We ensure that students receive the most effective CAT exam preparation materials with our CAT preparation module. The BYJU’S (the Best App for CAT preparation) module is compiled in accordance with all the latest CAT changes and updates given by the IIM-CAT authorities. The CAT 2023 aspirants can go through various interactive video lessons to learn in an effective way.
CAT Study Material for Exam Preparation
Get our free CAT preparation material, which includes interactive video lessons, shortcut tips and tricks to start your CAT Exam preparation from scratch.
Tips on How to Prepare for CAT Exam
There are a lot of things to consider as you prepare for the examination, and you may be unsure as to where and how to begin. Check out these expert tips as you get started with your CAT preparation.
- Time management is an important factor to be considered right from the start of your CAT preparation. You have a sectional time limit of 40 minutes. During your preparation, keep track of the time taken to solve each question. As you progress, work on improving your speed and accuracy.
- Using shortcut techniques to solve questions saves a great deal of time. Keep in mind the shortcut CAT Preparation tips and tricks that your mentors teach you, and make sure you note them down and review them on a regular basis.
- Practising previous years’ question papers and mock tests helps you identify your strengths and weaknesses.
- One of the most important factors in cracking CAT is the choice of questions. Make sure you analyse a question carefully before you attempt it, and go forward only if you are confident enough to solve it.
- To improve your vocabulary and reading skills, read books, editorials, newspapers, and journals.
CAT Exam Preparation Tips & Tricks Related Resources
Below we have listed some important CAT preparation links. The candidates can follow these tips and tricks for CAT exam preparation to score a good rank in the upcoming exam.
Best Online Videos for CAT Preparations
Our CAT exam preparation module is compiled keeping in mind all the latest changes and updates brought about by the IIM-CAT authorities. We make sure that our students get the best CAT preparation materials. The exam aspirants can go through various interactive video lessons and start CAT Preparation in an effective and scheduled way.





CAT Preparation – Explore with BYJU’S
The aspirants can explore CAT exam preparation tips with BYJJU’S and start preparing as soon as possible. Our exam experts provide the best and most result-oriented CAT study plan for all three exam sections.
| CAT Preparation with Tablet Learning Program | Admission Counselling |
| Basics and Concept Visualisation | Expert suggestions for the correct selection of B-schools |
| Engaging Videos with Adaptive Learning | Numerous workshops for regular academic counselling |
| Personalised Mentoring and Doubt Clearing Sessions | No partner universities |
| Numerous Test Series | Personalised mentorship with IIM Alumni |
| Peerless Faculty | Extended guidance to help you identify the weak and strong areas of your personality to ace the GD-PI round. |
With our free CAT preparation, you will be able to complete the entire CAT syllabus, along with various CAT mock tests and other CAT preparation material like video lectures, question papers, test series, topic-specific articles, textbooks, etc. Your CAT 2023 journey is made seamless and enjoyable with India’s best online platform for CAT preparation.
CAT exam preparation needs to be done on a consistent and regular basis to retain the concepts efficiently. We focus on improving the aspirant’s basics first. With BYJU’S CAT Preparation Tablet, candidates get access to 300+ engaging videos (130+ hrs) and 135+ LIVE sessions by IIM Alumni and serial 99 percentile achievers.
How to Prepare for CAT by Self-Study
Self-study for CAT exam preparation is an important factor. The candidates must do self-study for each of the chapters although they have joined coaching institutes for preparation.
- CAT preparation by self-study boosts candidates’ confidence in enhancing their knowledge.
- It enhances their problem-solving skills which is extremely important to crack CAT with a decent score.
- Self-studying is always flexible and the students can do their CAT preparation anywhere from their comfort zone.
- It inspires curiosity in candidates and motivates them always to do better by optimizing their previous mistakes.
BYJU’S CAT Exam Preparation Tablet: Program Details
Candidates can enroll in BYJU’S tablet course for an efficient coaching experience with the best CAT trainers in the country. With BYJU’S shortcut tricks and tips for CAT exam preparation, one can be sure to ace any management-level exam easily. Below you can find a list of detailed features relating to BYJU’S tablet for CAT Preparation.
| CAT Preparation Tablet | Features |
| LIVE Classes | With more than 135+ Live Sessions, students get the opportunity to interact with faculty and get all their doubts answered. |
| Mentorship Program | Students can keep track of their progress through the Personal Mentorship Program. Professional guidance is incorporated into the study regimens of the CAT preparation program. |
| Recorded Videos | The recorded videos are what make the product stand out. Basic and advanced topics are discussed in these videos. Students gain access to 300+ engaging videos (130+hrs) on the CAT Tab with sessions by Byju Raveendran, who aced the CAT with the 100 percentile. |
| Time Management Skills | Discover simple shortcuts and strategies that are designed and compiled by India’s No.1 CAT experts. This will help you answer any question, no matter how challenging, within the time schedule. |
| Study Notes & Books | Complete CAT study material, notes and PDFs can be accessed conveniently. These detailed notes will help you gain a comprehensive knowledge of the major concepts and topics covered in the exam |
| Mock Tests | With the CAT Mock Tests, based on the latest exam pattern with video solutions and video attempts by IIM Alumni, you will get the chance to analyse your performance along with the video attempts. |
| Practice Questions & Sectional Tests | The most comprehensive part of this program is the repository of 9500+ topic-wise Practice Questions. Also included are 25 Sectional Tests for CAT, along with sectional practice questions. |
| GD/PI preparation Mentorship with IIM Alumni | Group Discussions and Personal Interviews are the final step towards achieving your B-School dream. This module includes 5 LIVE sessions, 12 recorded sessions, mock interviews, current affairs notes, and more to prepare you for the GD-PI process. Now that digital technology has become part of our everyday lives, CAT preparation has never been easier. The BYJU’S Tablet Learning program enables you to prepare for the CAT with just a click of a button. |
Teaching Methodology of BYJU’S CAT Preparation Tablet
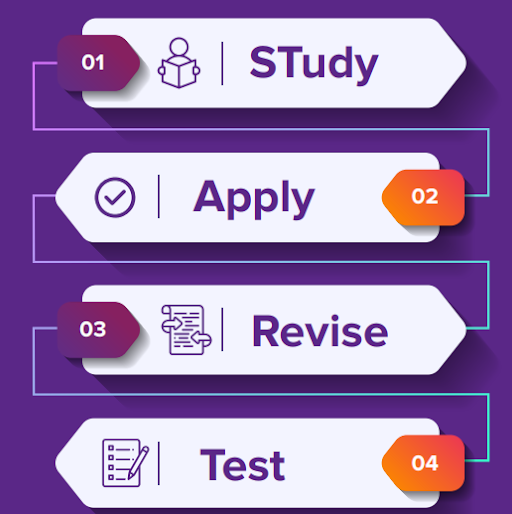
To ensure in-depth conceptual clarity and effective CAT exam preparation, BYJU’S Preparation Tablet incorporates the START Methodology. Preparing for CAT in this manner helps students succeed in the B-School selection process and cut through the competition. Given below is an illustration of how the start methodology works.
Distinctive Features of BYJU’S CAT Preparation Tablet:
- In addition to the last ten years’ solved papers, the tablet also provides aspirants with a detailed overview of recent year’s examination papers.
- This interactive module for CAT Preparation is exclusively designed to develop and enhance the concepts of Verbal Ability, Quantitative Aptitude, Logical Reasoning and Data Interpretation.
- The best quality study materials, including 14 CAT books with 13 chapter-wise reference study materials and 1 CAT worksheet, are provided. Each chapter in the book begins with a brief description of the concepts covered in the tablet, as well as an overview of the point-wise importance of topics covered in the book.
- The 200 unit tests and 20 mock tests provided will ensure your confidence is at its peak during the exam.
- Practice exercises at the end of each chapter will help you to improve your self-analysis and aid in revising the topics.
- There are shortcut techniques that can make it easier to comprehend the principles that are based on the questions. These techniques can be used while practising the questions.
CAT Exam Preparation with Last Years Exam Papers
The previous years’ exam papers are the most important study resources. It helps the candidates to know the latest changes in the exam, test structures and important topics. So, the candidates’ first priority during CAT preparation should be to solve the previous year’s papers without any forget.
Here, we have provided the last year’s questions papers PDF for your easy reference.
- CAT 2022 Question Paper PDF Download
- CAT 2021 Question Paper PDF Download
- CAT 2020 Question Paper PDF Download
- CAT 2019 Question Paper PDF Download
- CAT 2018 Question Paper PDF Download
- CAT 2017 Question Paper PDF Download
Aspirants who are interested in enrolling in our CAT preparation module, which includes study materials and a tablet, can reach our educational counsellor at 09880031619. Additionally, to give candidates a better clarity of the CAT 2023 exam, we also provide the most recent information for CAT, regarding syllabus, pattern, exam dates and more.
Frequently Asked Questions on CAT Preparation
How often should I practise mock tests and sample questions?
Practice is the key to ace the CAT Exam. You can become more familiar with the exam pattern by taking mock tests regularly. They will also help you gain a better understanding of what to expect from the real exam and improve your speed. Once you are strong with the fundamentals, it is recommended to take one sectional mock every day, followed by an overall mock once every four days.
What are the benefits of joining CAT Coaching?
It is important to have adequate learning resources and expert guidance while preparing for the CAT Exam. An online coaching program will give you access to exclusive preparation resources. Regular mock tests and personal mentoring provide you with detailed feedback on your progress throughout the course. If you are unable to attend a live class taught by the CAT Experts, you may watch the recorded classes, at your convenience.
How to prepare for CAT Quantitative Aptitude section?
The QA section consists of about 22 questions. This section covers a variety of topics from Arithmetic, Algebra, Modern Maths, Geometry, Mensuration, etc. Set a timetable for your preparation beforehand. Prior to moving into the advanced topics, it is essential that you understand the fundamentals. Make it a habit to note the shortcuts and techniques that your mentors have taught you. Make the best use of the past years’ papers to get better insights into this section.
Which is the best app for CAT Preparation?
The BYJU’S – the Learning App, is the best app for CAT preparation. It provides the best online platform for exam preparation to all its students.