Geometry is the branch of mathematics that deals with shapes, angles, dimensions and sizes of a variety of things we see in everyday life. Geometry is derived from Ancient Greek words – ‘Geo’ means ‘Earth’ and ‘metron’ means ‘measurement’. In Euclidean geometry, there are two-dimensional shapes and three-dimensional shapes.
In a plane geometry, 2d shapes such as triangles, squares, rectangles, circles are also called flat shapes. In solid geometry, 3d shapes such as a cube, cuboid, cone, etc. are also called solids. The basic geometry is based on points, lines and planes explained in coordinate geometry.
The different types of shapes in geometry help us to understand the shapes day to day life. With the help of geometric concepts, we can calculate the area, perimeter and volume of shapes.
| Table of Contents: |
Geometry Definition
Geometry is the study of different types of shapes, figures and sizes in Maths or in real life. In geometry, we learn about different angles, transformations and similarities in the figures.
The basics of geometry depend on majorly point, line, angles and plane. All the geometrical shapes are based on these basic geometrical concepts.
Branches of Geometry
The branches of geometry are categorized as:
- Algebraic geometry
- Discrete geometry
- Differential geometry
- Euclidean geometry
- Convex geometry
- Topology
Algebraic Geometry
It is a branch of geometry studying zeros of the multivariate polynomial. It includes linear and polynomial algebraic equations that are used for solving the sets of zeros. The application of this type comprises Cryptography, string theory, etc.
Discrete Geometry
It is concerned with the relative position of simple geometric objects, such as points, lines, triangles, circles etc.
Differential Geometry
It uses techniques of algebra and calculus for problem-solving. The various problems include general relativity in physics etc.
Euclidean Geometry
The study of plane and solid figures based on axioms and theorems including points, lines, planes, angles, congruence, similarity, solid figures. It has a wide range of applications in Computer Science, Modern Mathematics problem solving, Crystallography etc.
Convex Geometry
It includes convex shapes in Euclidean space using techniques of real analysis. It has application in optimization and functional analysis in number theory.
Topology
It is concerned with the properties of space under continuous mapping. Its application includes consideration of compactness, completeness, continuity, filters, function spaces, grills, clusters and bunches, hyperspace topologies, initial and final structures, metric spaces, nets, proximal continuity, proximity spaces, separation axioms, and uniform spaces.
Also, check: Analytic geometry
Geometry Formulas
To calculate the area, perimeter, volume and different measures using length, breadth and height of different geometrical figures, geometry formulas are important. By using the formulas, we can calculate the measures easily. There are loads of formulas to learn in Geometry. Here, you are provided with all the important geometry formulas in the PDF. Download the below-given PDF to learn and solve all the problems related to geometry.
Geometry Formulas:-Download PDF Here
Plane Geometry (Two-dimensional Geometry)
Plane Geometry deals with flat shapes which can be drawn on a piece of paper. These include lines, circles & triangles of two dimensions. Plane geometry is also known as two-dimensional geometry.
All the two-dimensional figures have only two measures such as length and breadth. It does not deal with the depth of the shapes. Some examples of plane figures are square, triangle, rectangle, circle, and so on.
The important terminologies in plane geometry are:
- Point
- Line
- Angles
Point
A point is a precise location or place on a plane. A dot usually represents them. It is important to understand that a point is not a thing, but a place. Also, note that a point has no dimension; preferably, it has the only position.
Line
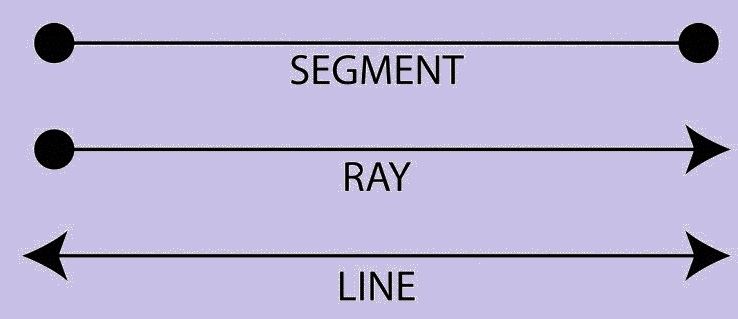
The line is straight (no curves), having no thickness and extends in both directions without end (infinitely). It is important to note that it is the combination of infinite points together to form a line. In geometry, we have a horizontal line and vertical line which are x-axis and y-axis respectively.
-
-
- Line Segment – If a line has a starting and an endpoint then it is called a Line Segment.
- Ray – If a line has a starting point and has no endpoint is called Ray.
-
Angles in Geometry
In planar geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
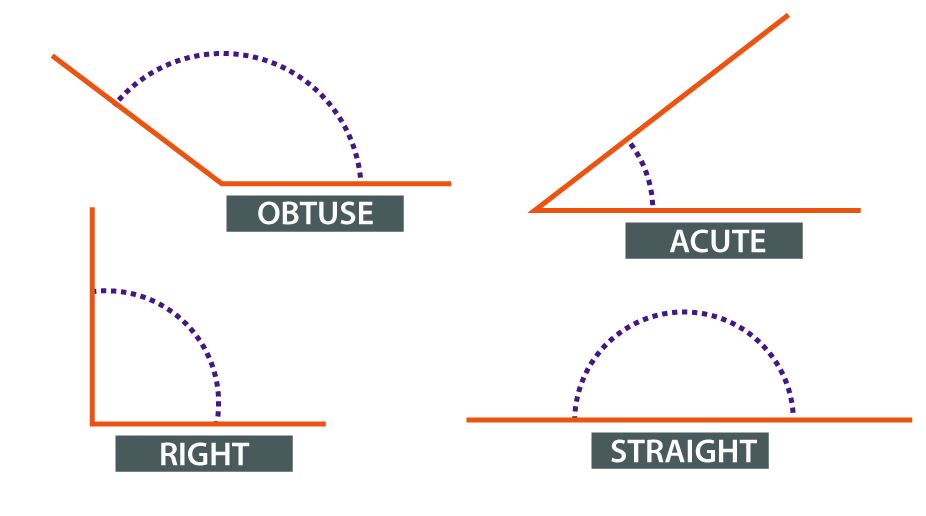
Types of Angle
Acute Angle – An Acute angle (or Sharp angle) is an angle smaller than a right angle ie. it can range between 0 – 90 degrees.
Obtuse Angle – An Obtuse angle is more than 90 degrees but is less than 180 degrees.
Right Angle – An angle of 90 degrees.
Straight Angle – An angle of 180 degrees is a straight angle, i.e. the angle formed by a straight line
Polygons in Geometry
A plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed polygonal chain or circuit.
The name ‘poly’ refers to multiple. An n-gon is a polygon with n sides; for example, a triangle is a 3-gon polygon.
General Formula for Sum of internal Angles of a polygon –
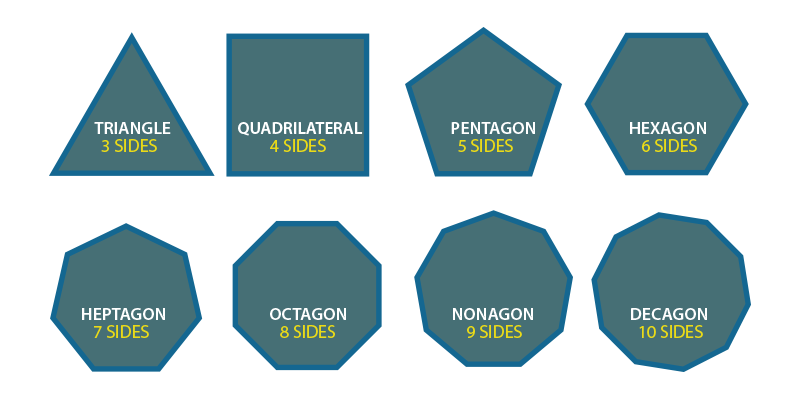
Types of Polygon
The types of polygons are:
- Triangles
- Quadrilaterals
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Nonagon
- Decagon
| Polygon type | Definition & Property | Types |
| (i) Triangle – | A 3-sided polygon whose sum of internal angles always sums to 180 degrees. |
|
| (ii) Quadrilateral | A 4-sided polygon with four edges and four vertices.
Sum of internal angles is 360 degrees |
|
| (iii) Pentagon | A plane figure with five straight sides and five angles | – |
| (iv) Hexagon | A plane figure with six straight sides and six angles | – |
| (v) Heptagon | A plane figure with seven sides and seven angles | – |
| (vi) Octagon | A plane figure with eight straight sides and eight angles. | – |
| (vii) Nonagon | A plane figure with nine straight sides and nine angles. | – |
| (viii) Decagon | A plane figure with ten straight sides and ten angles. | – |
In the below figure, we can see the different types of polygons.
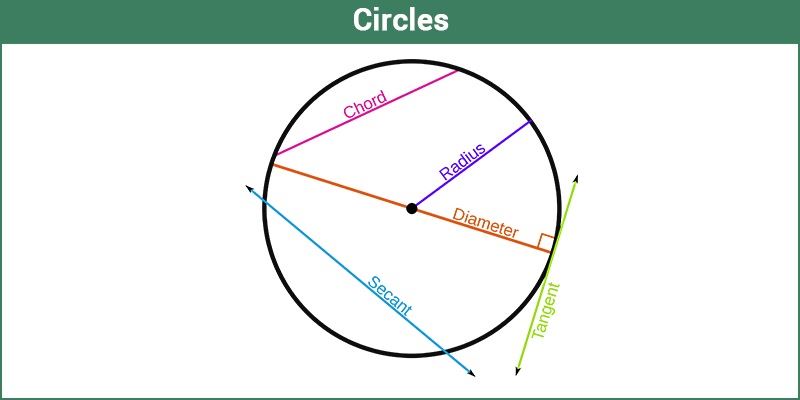
Circle in Geometry
A Circle is a simple closed shape. From a certain point called the centre, all points of a circle are of same consistent distance, i.e. the curve traced out by a point that moves so that its distance from the centre is constant.
 Similarity and Congruency in Geometry
Similarity and Congruency in Geometry
Similarity – Two figures are said to be similar if they have the same shape or have an equal angle but do not have the same size.
Congruence – Two figures are said to be Congruent if they have the same shape and size. Thus, they are totally equal.
Solid Geometry (Three-dimensional geometry)
Solid Geometry deals with 3-dimensional objects like cubes, prisms, cylinders & spheres. It deals with three dimensions of the figure such as length, breadth and height. But some solid solids do not have faces (e.g. sphere).
Solid geometry is the study of three dimensions in Euclidean space. The objects which are around us are three-dimensional. All the three-dimensional shapes are obtained from the rotation operation of 2D shapes. The important attributes of 3D shapes are:
- Faces
- Edges
- Vertices
Go through these terms in detail for different geometric shapes here.
Edges
An edge is defined as the line segment on the boundary that joins one vertex to the other vertex. It means that it joins one corner point to the other. It forms the skeleton of 3D shapes. In other words, it can be defined as the faces, that meet in the straight line is called edge. Following are the list of edges for the different solid shapes:
|
Solid Shapes |
No. of. Edges |
|
Triangular Prism |
9 |
|
Cube |
12 |
|
Rectangular prism |
12 |
|
Pentagonal Prism |
15 |
|
Hexagonal Prism |
18 |
|
Triangular Pyramid |
6 |
|
Square Pyramid |
8 |
|
Pentagonal Pyramid |
10 |
|
Hexagonal Pyramid |
12 |
Faces
We know that all the geometric shapes are made up of flat surface called faces. It is a flat surface enclosed by the edges. For any three-dimensional shapes, the face should be a two-dimensional figure. The list of the number of faces for different solid shapes are given below:
|
Solid Shapes |
No. of. Faces |
|
Triangular Prism |
5 |
|
Cube |
6 |
|
Rectangular prism |
6 |
|
Pentagonal Prism |
7 |
|
Hexagonal Prism |
8 |
|
Triangular Pyramid |
4 |
|
Square Pyramid |
5 |
|
Pentagonal Pyramid |
6 |
|
Hexagonal Pyramid |
7 |
Vertices
A vertex is defined as the point where the edges of the solid figure meet at each other. In other words, it can be said that, the point where the adjacent sides of the polygon meet. The vertex is the corners where the edges meet. The number of vertices for different solid shapes in geometry is as follows:
|
Solid Shapes |
No. of. Vertices |
|
Triangular Prism |
6 |
|
Cube |
8 |
|
Rectangular prism |
8 |
|
Pentagonal Prism |
10 |
|
Hexagonal Prism |
12 |
|
Triangular Pyramid |
4 |
|
Square Pyramid |
5 |
|
Pentagonal Pyramid |
6 |
|
Hexagonal Pyramid |
7 |
Geometry Related Articles
Video Lesson
Combination to form Geometry Models

Frequently Asked Questions of Geometry
How geometry is used?
Geometry is used in configuring and measurement of different shapes and sizes, such as circles, squares, cubes, triangles, etc.
What are all the Geometry applications?
Geometry has wide usage in daily life. Its major applications are in the field of constructions, such as the construction of building, roads, dams, bridges, etc. and also in surveying, mapping, navigation. In software industries, it is used in graphics designing, gaming, animations, etc. In the medical field as well, for CT scanning and MRI’s geometry concepts are used.
Why geometry is important?
In our lives, geometry is important to understand the various shapes and measure them based on area and volumes.
What geometry means?
Geometry means the measurement of Earth, as it derived from the ancient Greek words, ‘geo’ means Earth and ‘metron’ means measurement. So any object which is present on earth has a shape which is defined by geometry.



It is a nice app to learn
Thank you, it’s a very nice app. It helps me a lot in my classes.
😀
Its is really good app for learning