Volume of a Triangular Prism Formula
A prism that has 3 rectangular faces and 2 parallel triangular bases, then it is a triangular prism. The triangular bases are joined by lateral faces and are parallel to each other. The space occupied by the triangular prism is the volume of the triangular prism.
The picture below illustrates the triangular prism which will help in deriving the formula. Let’s solve one example.
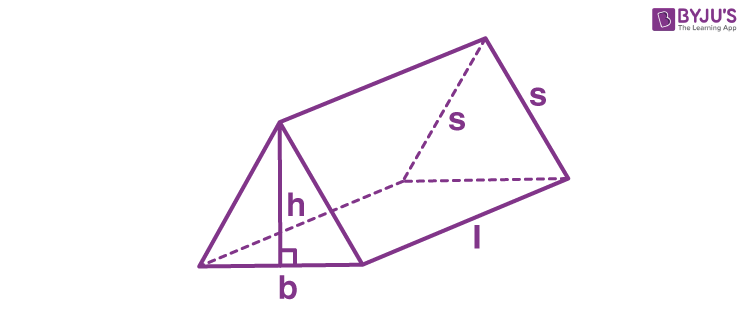
\[\large Volume\;of\;triangular\;prism=\frac{1}{2}bhl\]
i.e. Volume of a triangular prism = Base area × Height of the prism
Solved Example
Question. Find out the volume of a triangular prism with the base of altitude 4 cm, side 3 cm and height of the prism is 6 cm
Solution:
Given,
b = 3 cm
h = 4 cm
l = 6 cm
According to the formula,
\(\begin{array}{l}Volume\;of\;triangular\;prism=\frac{1}{2}blh\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\times3\times4\times6\end{array} \)
\(\begin{array}{l}=36 cm^{3}\end{array} \)
Comments