AP Board Class 9 Maths Chapter 4 Lines and Angles

Andhra Pradesh board Class 9 students, studying Maths will come across the topic of lines and angles in Chapter 4. This AP Board Class 9 Maths Chapter 4 Lines and Angles has been structured to help students become familiar with the concepts of lines and angles. In this Chapter 4 of AP Board Class 9 Maths, students will also learn the definition of some basic terms in Geometry and also understand some theorems. Important topics discussed in the chapter include;

• Intersecting Lines And Non-intersecting Lines
• Pairs Of Angles
• Linear Pair Of Angles Axiom
• Lines And A Transversal
• Angle Sum Property Of A Triangle

Lines

In Geometry, lines are figures consisting of infinite points, which extend indefinitely in both directions. Lines are usually straight and do not have depth or width.

A line segment is a part of a line having two endpoints. It is the shortest distance between two points and has a fixed length. A ray is a part of a line having a starting point but no endpoint. It goes on endlessly in a certain direction. Whenever there are three or more points that exist on the same line it is known as collinear points. While points that do not lie on the same line are called non-collinear points. Topics discussed in this section includes

• Intersecting Lines and Non-Intersecting Lines
• Concurrent Lines

Angles

An angle is a figure obtained when two rays appear from a common point. There are various types of angles, namely right, acute, obtuse, reflex, straight, adjacent, complementary and supplementary angles.

Linear Pair Of Angles Axiom

Linear pair axiom: The sum of the two adjacent angles formed is 180^o if a ray stands on a straight line.

Converse of linear pair axiom: Non-common arms of the angles usually form a line if the sum of two adjacent angles is 180^o.

Students can look at some of the chapter questions along with their solutions below;

Question 1: Two complementary angles are in the ratio 4:5. Find the angles.

Solution: Let the required angles be 4x and 5x.

Then 4x + 5x = 90^o

9x = 90^o

X = 90/9

x = 10^o

Hence the required angles are 40^o and 50^o.

Question 2: In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135^o and ∠PQT = 110^o, find ∠PRQ.

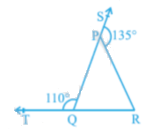
From the figure, we can conclude that

∠SPR and ∠RPQ, and ∠SPR and ∠RPQ form a linear pair.

We know that the sum of angles of a linear pair is 180^o

∠SPR + ∠RPQ = 180^o, and

∠PQT + ∠PQR = 180^o.

1350 + ∠RPQ = 180^o, and

1100 + ∠PQR = 180^o, or

∠RPQ = 45^o, and

∠PQR = 70^o.

From the figure, we can conclude that

∠PQR + ∠RPQ + ∠PRQ = 180^o. (Angle sum property)

⇒ 70^o + 45^o + ∠PRQ = 180^o ⇒ 115^o + ∠PRQ = 180^o

⇒ ∠PRQ = 65^o.

Therefore, we can conclude that ∠PRQ = 65^o.

Get to know more about AP SSC Board and access various study materials including syllabus, exam timetable and more by visiting BYJU’s regularly.

Also Read;