Basic Math Formula: Let us discuss here the general formulas used in basic Maths, which are used not only in academic books but also in our day to day life. In your primary classes, you must have learned the general BODMAS rule. But as you approach higher classes from 6 to 10, you will come across various mathematic formulas based on different concepts such as Algebra. By practising questions and answers based on these formulas, you can by-heart them. Some of the other concepts which have formulas are:
- Fractions
- Percentage
- Formula for proportion
- Geometry
- Trigonometric formulas and many more
Basic Maths
The basic of Maths display how a math problem can be solved with the help of some equations such as the equation of forces, accelerations or work done. More importantly, they are used to provide mathematical solutions for real-world problems.
There are many types of equations, and they are found in many areas of mathematics. The techniques used to examine them differ according to their type. It can be as simple as a basic addition formula or complicated as the integration of differentiation.
Basic Maths Formulas List
Some of the Basic Math Formulas lists are given below:

In proportion, the product of the extremes (ad) equals the product of the means(bc). Thus, ad = bc
Percentage Formulas
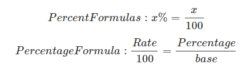
Where,
Rate = Percent
Base = The amount you are taking the percent of
Percentage = The answer obtained by multiplying the base by the rate
Basic Math Questions
Question 1: Find x, if 1/5 = 2/x.
Solution: Given, 1/5 = 2/x
On cross multiplication, we get,
1 × x = 2 × 5
⇒ x = 10
Solution:
byju ‘s is the best place of online study
Best platform for online learning
Best platform for online learning
AN ACTIVE APP FOR STUDENTS AND NEET , JEE CLASSES.