If the two vectors are assumed as
\(\begin{array}{l}\vec{a}\end{array} \)
and \(\begin{array}{l}\vec{b}\end{array} \)
then the dot created is articulated as \(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
. Let’s suppose these two vectors are separated by angle θ. To know what’s the angle measurement we solve with the below formula
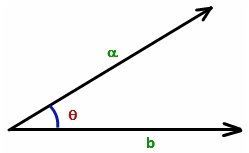
we know that the dot product of two product is given as
\(\begin{array}{l}\vec{a}.\vec{b} =|\vec{a}||\vec{b}|cos\theta\end{array} \)
Thus, the angle between two vectors formula is given by
\(\begin{array}{l}\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\end{array} \)
where θ is the angle between
\(\begin{array}{l}\vec{a}\end{array} \)
and \(\begin{array}{l}\vec{b}\end{array} \)
Angle Between Two Vectors Examples
Let’s see some samples on the angle between two vectors:
Example 1:
Compute the angle between two vectors 3i + 4j – k and 2i – j + k.
solution:
Let
\(\begin{array}{l}\vec{a}\end{array} \)
= 3i + 4j – k and
\(\begin{array}{l}\vec{b}\end{array} \)
= 2i – j + k
The dot product is defined as
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= (3i + 4j – k).(2i – j + k)
= (3)(2) + (4)(-1) + (-1)(1)
= 6-4-1
= 1
Thus,
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= 1
The Magnitude of vectors is given by
\(\begin{array}{l}|\vec{a}| =\sqrt{(3^{2}+4^{2}+(-1)^{2})} =\sqrt{26}= 5.09\end{array} \)
\(\begin{array}{l}|\vec{b}| =\sqrt{(2^{2}+(-1)^{2}+1^{2})} =\sqrt{6}= 2.45\end{array} \)
The angle between the two vectors is
\(\begin{array}{l}\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}\frac{1}{(5.09)(2.45)}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}\frac{1}{12.47}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}(0.0802)\end{array} \)
\(\begin{array}{l}\theta = 85.39^{\circ}\end{array} \)
Example 2:
Find the angle between two vectors 5i – j + k and i + j – k.
Solution:
Let
\(\begin{array}{l}\vec{a}\end{array} \)
= 5i – j + k and
\(\begin{array}{l}\vec{b}\end{array} \)
= i + j – k
The dot product is defined as
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= (5i – j + k)(i + j – k)
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= (5)(1) + (-1)(1) + (1)(-1)
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= 5-1-1
\(\begin{array}{l}\vec{a}. \vec{b}\end{array} \)
= 3
The Magnitude of vectors is given by
\(\begin{array}{l}|\vec{a}| =\sqrt{(5^{2}+(-1)^{2}+1^{2})} =\sqrt{27}= 5.19\end{array} \)
\(\begin{array}{l}|\vec{b}| =\sqrt{(1^{2}+1^{2}+(-1)^{2})} =\sqrt{3}= 1.73\end{array} \)
The angle between the two vectors is
\(\begin{array}{l}\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}\frac{3}{(5.19)(1.73)}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}\frac{3}{8.97}\end{array} \)
\(\begin{array}{l}\theta = cos^{-1}(0.334)\end{array} \)
\(\begin{array}{l}\theta =70.48^{\circ}\end{array} \)
To learn more formulas on different concepts, visit BYJU’S – The Learning App and download the app to learn with ease.

Comments