*According to the CBSE Syllabus 2023-24, this chapter has been removed.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions are provided in a detailed manner, where students can find a step-by-step solution to all the questions for fast revisions. Solutions for the 11th chapter of NCERT Class 10 Maths are prepared by subject experts under the guidelines of the NCERT to assist students in their board exam preparations. Get free NCERT Solutions for Class 10 Maths, Chapter 11 – Constructions at BYJU’S to accelerate the CBSE exam preparation. All the questions of NCERT exercises are solved using diagrams with a step-by-step procedure for construction. Solutions of NCERT help students boost their concepts and clear doubts.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions
Access Answers to Maths NCERT Chapter 11 – Constructions
Exercise 11.1 Page: 220
In each of the following, give the justification for the construction also.
1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Construction Procedure
A line segment with a measure of 7.6 cm length is divided in the ratio of 5:8 as follows.
1. Draw line segment AB with a length measure of 7.6 cm.
2. Draw a ray AX that makes an acute angle with line segment AB.
3. Locate the points, i.e.,13 (= 5+8) points, such as A1, A2, A3, A4 …….. A13, on the ray AX, such that it becomes AA1 = A1A2 = A2A3 and so on.
4. Join the line segment and the ray, BA13.
5. Through the point A5, draw a line parallel to BA13 which makes an angle equal to ∠AA13B.
6. Point A5, which intersects line AB at point C.
7. C is the point that divides line segment AB of 7.6 cm in the required ratio of 5:8.
8. Now, measure the lengths of the line AC and CB. It becomes the measure of 2.9 cm and 4.7 cm, respectively.
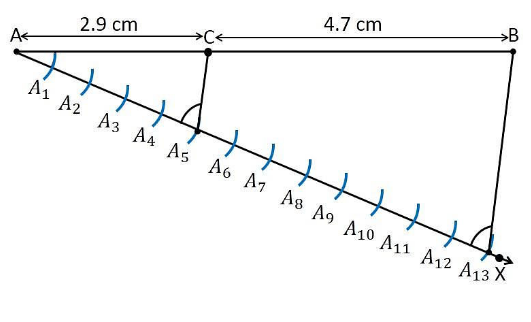
Justification:
The construction of the given problem can be justified by proving that
AC/CB = 5/ 8
By construction, we have A5C || A13B. From the Basic proportionality theorem for the triangle AA13B, we get
AC/CB =AA5/A5A13….. (1)
From the figure constructed, it is observed that AA5 and A5A13 contain 5 and 8 equal divisions of line segments, respectively.
Therefore, it becomes
AA5/A5A13=5/8… (2)
Compare the equations (1) and (2), we obtain
AC/CB = 5/ 8
Hence, justified.
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of
the corresponding sides of the first triangle.
Construction Procedure
1. Draw a line segment AB which measures 4 cm, i.e., AB = 4 cm.
2. Take point A as the centre, and draw an arc of radius 5 cm.
3. Similarly, take point B as its centre, and draw an arc of radius 6 cm.
4. The arcs drawn will intersect each other at point C.
5. Now, we have obtained AC = 5 cm and BC = 6 cm, and therefore, ΔABC is the required triangle.
6. Draw a ray AX which makes an acute angle with the line segment AB on the opposite side of vertex C.
7. Locate 3 points such as A1, A2, and A3 (as 3 is greater between 2 and 3) on line AX such that it becomes AA1= A1A2 = A2A3.
8. Join point BA3 and draw a line through A2, which is parallel to the line BA3 that intersects AB at point B’.
9. Through the point B’, draw a line parallel to line BC that intersects the line AC at C’.
10. Therefore, ΔAB’C’ is the required triangle.

Justification
The construction of the given problem can be justified by proving that
AB’ = (2/3)AB
B’C’ = (2/3)BC
AC’= (2/3)AC
From the construction, we get B’C’ || BC
∴ ∠AB’C’ = ∠ABC (Corresponding angles)
In ΔAB’C’ and ΔABC,
∠ABC = ∠AB’C (Proved above)
∠BAC = ∠B’AC’ (Common)
∴ ΔAB’C’ ∼ ΔABC (From AA similarity criterion)
Therefore, AB’/AB = B’C’/BC= AC’/AC …. (1)
In ΔAAB’ and ΔAAB,
∠A2AB’ =∠A3AB (Common)
From the corresponding angles, we get
∠AA2B’ =∠AA3B
Therefore, from the AA similarity criterion, we obtain
ΔAA2B’ and AA3B
So, AB’/AB = AA2/AA3
Therefore, AB’/AB = 2/3 ……. (2)
From equations (1) and (2), we get
AB’/AB=B’C’/BC = AC’/ AC = 2/3
This can be written as
AB’ = (2/3)AB
B’C’ = (2/3)BC
AC’= (2/3)AC
Hence, justified.
3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle
Construction Procedure
1. Draw a line segment AB =5 cm.
2. Take A and B as the centre, and draw the arcs of radius 6 cm and 7 cm, respectively.
3. These arcs will intersect each other at point C, and therefore, ΔABC is the required triangle with the length of sides as 5 cm, 6 cm, and 7 cm, respectively.
4. Draw a ray AX which makes an acute angle with the line segment AB on the opposite side of vertex C.
5. Locate the 7 points, such as A1, A2, A3, A4, A5, A6, A7 (as 7 is greater between 5 and 7), on line AX such that it becomes AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
6. Join the points BA5 and draw a line from A7 to BA5, which is parallel to the line BA5 where it intersects the extended line segment AB at point B’.
7. Now, draw a line from B’ to the extended line segment AC at C’, which is parallel to the line BC, and it intersects to make a triangle.
8. Therefore, ΔAB’C’ is the required triangle.
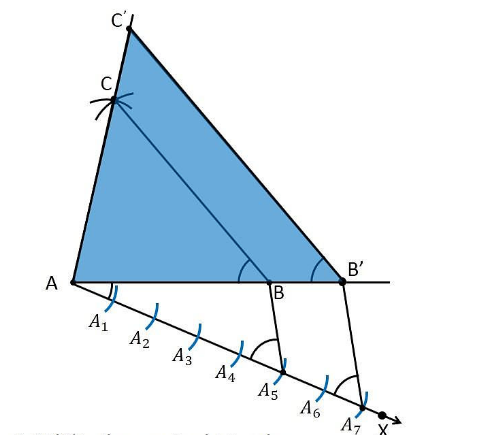
Justification
The construction of the given problem can be justified by proving that
AB’ = (7/5)AB
B’C’ = (7/5)BC
AC’= (7/5)AC
From the construction, we get B’C’ || BC
∴ ∠AB’C’ = ∠ABC (Corresponding angles)
In ΔAB’C’ and ΔABC,
∠ABC = ∠AB’C (Proved above)
∠BAC = ∠B’AC’ (Common)
∴ ΔAB’C’ ∼ ΔABC (From AA similarity criterion)
Therefore, AB’/AB = B’C’/BC= AC’/AC …. (1)
In ΔAA7B’ and ΔAA5B,
∠A7AB’=∠A5AB (Common)
From the corresponding angles, we get
∠A A7B’=∠A A5B
Therefore, from the AA similarity criterion, we obtain
ΔA A2B’ and A A3B
So, AB’/AB = AA5/AA7
Therefore, AB /AB’ = 5/7 ……. (2)
From equations (1) and (2), we get
AB’/AB = B’C’/BC = AC’/ AC = 7/5
This can be written as
AB’ = (7/5)AB
B’C’ = (7/5)BC
AC’= (7/5)AC
Hence, justified.
 Construction Procedure:
Construction Procedure:
1. Draw a line segment BC with a measure of 8 cm.
2. Now, draw the perpendicular bisector of the line segment BC and intersect at point D.
3. Take the point D as the centre and draw an arc with a radius of 4 cm, which intersects the perpendicular bisector at the point A.
4. Now, join the lines AB and AC, and the triangle is the required triangle.
5. Draw a ray BX which makes an acute angle with the line BC on the side opposite to the vertex A.
6. Locate the 3 points B1, B2 and B3 on the ray BX such that BB1 = B1B2 = B2B3
7. Join the points B2C and draw a line from B3, which is parallel to the line B2C where it intersects the extended line segment BC at point C’.
8. Now, draw a line from C’ to the extended line segment AC at A’, which is parallel to the line AC, and it intersects to make a triangle.
9. Therefore, ΔA’BC’ is the required triangle.

Justification
The construction of the given problem can be justified by proving that
A’B = (3/2)AB
BC’ = (3/2)BC
A’C’= (3/2)AC
From the construction, we get A’C’ || AC
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
In ΔA’BC’ and ΔABC,
∠B = ∠B (Common)
∠A’BC’ = ∠ACB
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Therefore, A’B/AB = BC’/BC= A’C’/AC
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
A’B/AB = BC’/BC= A’C’/AC = 3/2
Hence, justified.
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Construction Procedure
1. Draw a ΔABC with base side BC = 6 cm, and AB = 5 cm and ∠ABC = 60°.
2. Draw a ray BX which makes an acute angle with BC on the opposite side of vertex A.
3. Locate 4 points (as 4 is greater in 3 and 4), such as B1, B2, B3, B4, on line segment BX.
4. Join the points B4C and also draw a line through B3, parallel to B4C intersecting the line segment BC at C’.
5. Draw a line through C’ parallel to the line AC, which intersects the line AB at A’.
6. Therefore, ΔA’BC’ is the required triangle.

Justification
The construction of the given problem can be justified by proving that
Since the scale factor is 3/4, we need to prove
A’B = (3/4)AB
BC’ = (3/4)BC
A’C’= (3/4)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (Common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 3/4
Hence, justified.
6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC.
To find ∠C:
Given:
∠B = 45°, ∠A = 105°
We know that,
The sum of all interior angles in a triangle is 180°.
∠A+∠B +∠C = 180°
105°+45°+∠C = 180°
∠C = 180° − 150°
∠C = 30°
So, from the property of the triangle, we get ∠C = 30°
Construction Procedure
The required triangle can be drawn as follows.
1. Draw a ΔABC with side measures of base BC = 7 cm, ∠B = 45°, and ∠C = 30°.
2. Draw a ray BX that makes an acute angle with BC on the opposite side of vertex A.
3. Locate 4 points (as 4 is greater in 4 and 3), such as B1, B2, B3, B4, on the ray BX.
4. Join the points B3C.
5. Draw a line through B4 parallel to B3C, which intersects the extended line BC at C’.
6. Through C’, draw a line parallel to the line AC that intersects the extended line segment at C’.
7. Therefore, ΔA’BC’ is the required triangle.
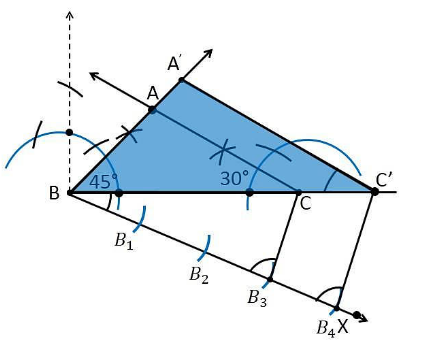
Justification
The construction of the given problem can be justified by proving that
Since the scale factor is 4/3, we need to prove
A’B = (4/3)AB
BC’ = (4/3)BC
A’C’= (4/3)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (Common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 4/3
Hence, justified.
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Given:
The sides other than the hypotenuse are of lengths 4cm and 3cm. It defines that the sides are perpendicular to each other
Construction Procedure
The required triangle can be drawn as follows.
1. Draw a line segment BC =3 cm.
2. Now, measure and draw an angle 90°
3. Take B as the centre and draw an arc with a radius of 4 cm, and intersects the ray at point B.
4. Now, join the lines AC, and the triangle ABC is the required triangle.
5. Draw a ray BX that makes an acute angle with BC on the opposite side of vertex A.
6. Locate 5 such as B1, B2, B3, B4, on the ray BX, such that BB1 = B1B2 = B2B3= B3B4 = B4B5
7. Join the points B3C.
8. Draw a line through B5 parallel to B3C, which intersects the extended line BC at C’.
9. Through C’, draw a line parallel to the line AC that intersects the extended line AB at A’.
10. Therefore, ΔA’BC’ is the required triangle.
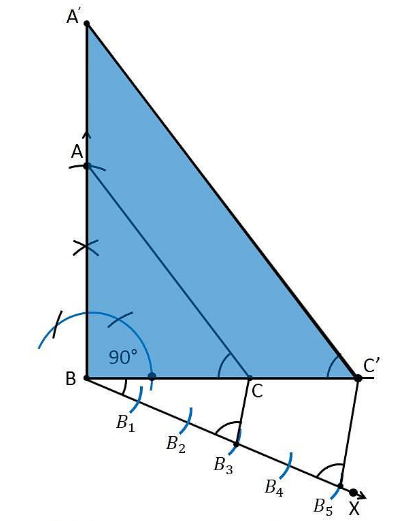
Justification
The construction of the given problem can be justified by proving that
Since the scale factor is 5/3, we need to prove
A’B = (5/3)AB
BC’ = (5/3)BC
A’C’= (5/3)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (Common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 5/3
Hence, justified.
Exercise 11.2 Page: 221
In each of the following, give the justification for the construction also.
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Construction Procedure
The construction to draw a pair of tangents to the given circle is as follows.
1. Draw a circle with a radius = 6 cm with centre O.
2. Locate a point P, which is 10 cm away from O.
3. Join points O and P through the line.
4. Draw the perpendicular bisector of the line OP.
5. Let M be the mid-point of the line PO.
6. Take M as the centre and measure the length of MO.
7. The length MO is taken as the radius, and draw a circle.
8. The circle drawn with the radius of MO intersect the previous circle at point Q and R.
9. Join PQ and PR.
10. Therefore, PQ and PR are the required tangents.
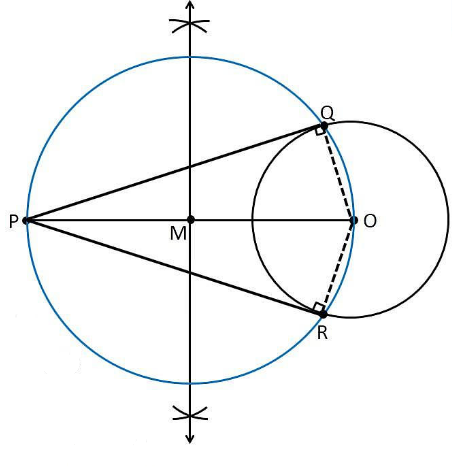
Justification
The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 6cm with centre O.
To prove this, join OQ and OR represented in dotted lines.
From the construction,
∠PQO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes
∴ ∠PQO = 90°
Such that
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with a radius of 6 cm, PQ must be a tangent of the circle. Similarly, we can prove that PR is a tangent of the circle.
Hence, justified.
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Construction Procedure
For the given circle, the tangent can be drawn as follows.
1. Draw a circle of 4 cm radius with centre “O”.
2. Again, take O as the centre and draw a circle of radius 6 cm.
3. Locate a point P on this circle.
4. Join the points O and P through lines, such that it becomes OP.
5. Draw the perpendicular bisector to the line OP
6. Let M be the mid-point of PO.
7. Draw a circle with M as its centre and MO as its radius,
8. The circle drawn with the radius OM intersects the given circle at the points Q and R.
9. Join PQ and PR.
10. PQ and PR are the required tangents.
From the construction, it is observed that PQ and PR are of length 4.47 cm each.
It can be calculated manually as follows:
In ∆PQO,
Since PQ is a tangent,
∠PQO = 90°. PO = 6cm and QO = 4 cm
Applying Pythagoras’ theorem in ∆PQO, we obtain PQ2+QO2 = PQ2
PQ2+(4)2 = (6)2
PQ2 +16 =36
PQ2 = 36−16
PQ2 = 20
PQ = 2√5
PQ = 4.47 cm
Therefore, the tangent length PQ = 4.47
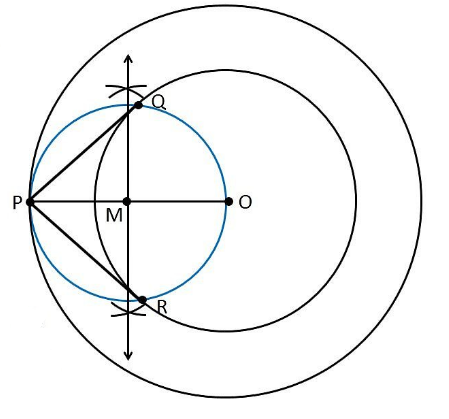
Justification
The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 4 cm with centre O.
To prove this, join OQ and OR represented in dotted lines.
From the construction,
∠PQO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes
∴ ∠PQO = 90°
Such that
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle with a radius of 4 cm, PQ must be a tangent of the circle. Similarly, we can prove that PR is a tangent of the circle.
Hence, justified.
3. Draw a circle of radius 3 cm. Take two points, P and Q, on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points, P and Q.
Construction Procedure
The tangent for the given circle can be constructed as follows.
1. Draw a circle with a radius of 3cm with a centre “O”.
2. Draw a diameter of a circle, and it extends 7 cm from the centre, and mark it as P and Q.
3. Draw the perpendicular bisector of the line PO and mark the midpoint as M.
4. Draw a circle with M as the centre and MO as the radius.
5. Now, join the points PA and PB in which the circle with radius MO intersects the circle of circle 3cm.
6. Now, PA and PB are the required tangents.
7. Similarly, from point Q, we can draw the tangents.
8. From that, QC and QD are the required tangents.
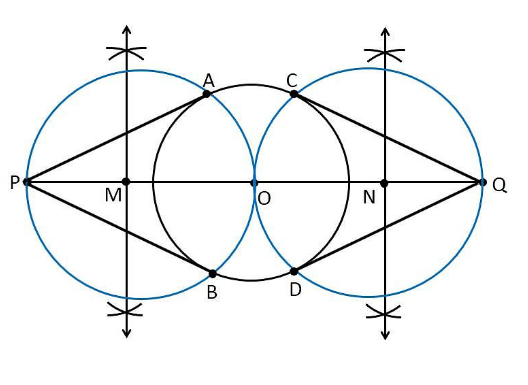
Justification
The construction of the given problem can be justified by proving that PQ and PR are the tangents to the circle of radius 3 cm with centre O.
To prove this, join OA and OB.
From the construction,
∠PAO is an angle in the semi-circle.
We know that angle in a semi-circle is a right angle, so it becomes
∴ ∠PAO = 90°
Such that
⇒ OA ⊥ PA
Since OA is the radius of the circle with a radius of 3 cm, PA must be a tangent of the circle. Similarly, we can prove that PB, QC and QD are the tangents of the circle.
Hence, justified.
4. Draw a pair of tangents to a circle of radius 5 cm, which are inclined to each other at an angle of 60°.
Construction Procedure
The tangents can be constructed in the following manner:
1. Draw a circle of radius 5 cm, with the centre as O.
2. Take a point Q on the circumference of the circle and join OQ.
3. Draw a perpendicular to QP at point Q.
4. Draw a radius OR, making an angle of 120°, i.e., (180°−60°) with OQ.
5. Draw a perpendicular to RP at point R.
6. Now, both the perpendiculars intersect at point P.
7. Therefore, PQ and PR are the required tangents at an angle of 60°.
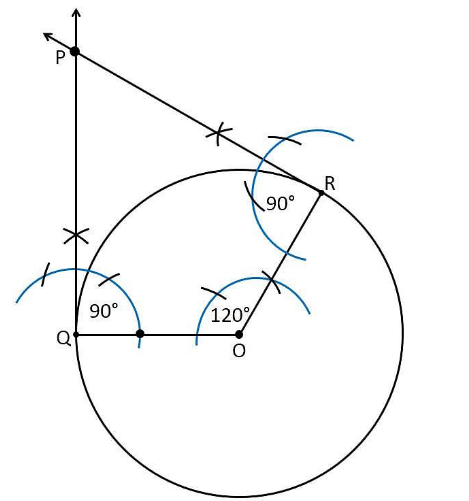
Justification
The construction can be justified by proving that ∠QPR = 60°.
By our construction,
∠OQP = 90°
∠ORP = 90°
And ∠QOR = 120°
We know that the sum of all interior angles of a quadrilateral = 360°
∠OQP+∠QOR + ∠ORP +∠QPR = 360o
90°+120°+90°+∠QPR = 360°
Therefore, ∠QPR = 60°
Hence, justified.
5. Draw a line segment AB of length 8 cm. Taking A as the centre, draw a circle of radius 4 cm and taking B as the centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Construction Procedure
The tangent for the given circle can be constructed as follows:
1. Draw a line segment AB = 8 cm.
2. Take A as the centre and draw a circle of radius 4 cm.
3. Take B as the centre and draw a circle of radius 3 cm.
4. Draw the perpendicular bisector of the line AB, and the midpoint is taken as M.
5. Now, take M as the centre and draw a circle with the radius of MA or MB, which intersects the circle at the points P, Q, R and S.
6. Now, join AR, AS, BP and BQ.
7. Therefore, the required tangents are AR, AS, BP and BQ.

Justification
The construction can be justified by proving that AS and AR are the tangents of the circle (whose centre is B with a radius of 3 cm), and BP and BQ are the tangents of the circle (whose centre is A and radius is 4 cm).
From the construction, to prove this, join AP, AQ, BS, and BR.
∠ASB is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠ASB = 90°
⇒ BS ⊥ AS
Since BS is the radius of the circle, AS must be a tangent of the circle.
Similarly, AR, BP, and BQ are the required tangents of the given circle.
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Construction Procedure
The tangent for the given circle can be constructed as follows:
1. Draw the line segment with base BC = 8cm.
2. Measure the angle 90° at the point B, such that ∠ B = 90°.
3. Take B as the centre and draw an arc with a measure of 6cm.
4. Let the point be A, where the arc intersects the ray.
5. Join the line AC.
6. Therefore, ABC is the required triangle.
7. Now, draw the perpendicular bisector to the line BC, and the midpoint is marked as E.
8. Take E as the centre, and BE or EC measure as the radius and draw a circle.
9. Join A to the midpoint E of the circle.
10. Now, again, draw the perpendicular bisector to the line AE, and the midpoint is taken as M.
11. Take M as the centre, and AM or ME measure as the radius and draw a circle.
12. This circle intersects the previous circle at points B and Q.
13. Join points A and Q.
14. Therefore, AB and AQ are the required tangents.

Justification
The construction can be justified by proving that AG and AB are the tangents to the circle.
From the construction, join EQ.
∠AQE is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠AQE = 90°
⇒ EQ⊥ AQ
Since EQ is the radius of the circle, AQ has to be a tangent of the circle. Similarly, ∠B = 90°
⇒ AB ⊥ BE
Since BE is the radius of the circle, AB has to be a tangent of the circle.
Hence, justified.
7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Construction Procedure
The required tangents can be constructed on the given circle as follows:
1. Draw a circle with the help of a bangle.
2. Draw two non-parallel chords, such as AB and CD.
3. Draw the perpendicular bisector of AB and CD.
4. Take the centre as O, where the perpendicular bisector intersects.
5. To draw the tangents, take a point P outside the circle.
6. Join points O and P.
7. Now, draw the perpendicular bisector of the line PO, and the midpoint is taken as M
8. Take M as the centre and MO as the radius and draw a circle.
9. Let the circle intersects intersect the circle at the points Q and R.
10. Now, join PQ and PR.
11. Therefore, PQ and PR are the required tangents.

Justification
The construction can be justified by proving that PQ and PR are tangents to the circle.
Since, O is the centre of a circle, we know that the perpendicular bisector of the chords passes through the centre.
Now, join the points OQ and OR.
We know that the perpendicular bisector of a chord passes through the centre.
It is clear that the intersection point of these perpendicular bisectors is the centre of the circle.
∠PQO is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠PQO = 90°
⇒ OQ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly,
∴ ∠PRO = 90°
⇒ OR ⊥ PO
Since OR is the radius of the circle, PR has to be a tangent of the circle.
Therefore, PQ and PR are the required tangents of a circle.
| Also Access |
| NCERT Exemplar for Class 10 Maths Chapter 11 |
| CBSE Notes for Class 10 Maths Chapter 11 |
NCERT Solutions for Class 10 Maths Chapter 11 Constructions
Topics present in NCERT Solutions for Class 10 Maths Chapter 11 include the division of a line segment, constructions of tangents to a circle, line segment bisector and many more. Students in Class 9 study some basics of constructions, like drawing the perpendicular bisector of a line segment, bisecting an angle, triangle construction etc. Using Class 9 concepts, students in Class 10 will learn more about constructions, along with the reasoning behind the work.
NCERT Class 10 Chapter 11-Constructions is a part of Geometry. Over the past few years, geometry has consisted of a total weightage of 15 marks in the final exams. Construction is a scoring chapter of the geometry section. In the previous year’s exam, one question of 4 marks was asked from this chapter.
List of Exercises in Class 10 Maths Chapter 11
Exercise 11.1 Solutions (7 Questions)
Exercise 11.2 Solutions (7 Questions)
The NCERT Solutions for Class 10 for the 11th chapter of Maths are all about the construction of line segments, division of a Line Segment and Construction of a Circle, Constructions of Tangents to a circle using an analytical approach. Students also have to provide a justification for each answer.
The topics covered in Maths Chapter 11 Constructions are:
| Exercise | Topic |
| 11.1 | Introduction |
| 11.2 | Division of a Line Segment |
| 11.3 | Construction of Tangents to a Circle |
| 11.4 | Summary |
Some of the ideas applied in this chapter are as follows:
- The locus of a point that moves at an identical distance from 2 points is normal to the line joining both points.
- Perpendicular or Normal means right angles, whereas the bisector cuts a line segment in two halves.
- The design of different shapes utilising a pair of compasses and a straightedge or ruler.
Key Features of NCERT Solutions for Class 10 Maths Chapter 11 Constructions
- NCERT solutions can also prove to be of valuable help to students in their assignments and preparation for CBSE and competitive exams.
- Each question is explained using diagrams which makes learning more interactive.
- Easy and understandable language is used in NCERT solutions.
- Solutions are provided using an analytical approach.
Disclaimer –
Dropped Topics –
11.1 Introduction
11.2 Division of a line segment
11.3 Construction of tangents into a circle
11.4 Summary
























good