Thermodynamics deals with the concepts of heat and temperature and the inter-conversion of heat and other forms of energy. The four laws of thermodynamics govern the behaviour of these quantities and provide a quantitative description. William Thomson, in 1749, coined the term thermodynamics.
What is Thermodynamics?
Thermodynamics in physics is a branch that deals with heat, work and temperature, and their relation to energy, radiation and physical properties of matter.
To be specific, it explains how thermal energy is converted to or from other forms of energy and how matter is affected by this process. Thermal energy is the energy that comes from heat. This heat is generated by the movement of tiny particles within an object, and the faster these particles move, the more heat is generated.

Thermodynamics is not concerned about how and at what rate these energy transformations are carried out. It is based on the initial and final states undergoing the change. It should also be noted that Thermodynamics is a macroscopic science. This means that it deals with the bulk system and does not deal with the molecular constitution of matter.
The video is a rapid revision of thermodynamics for JEE Main, presented by Rakhi Ma’am through short notes and previous year questions (PYQs).

Distinction Between Mechanics and Thermodynamics
The distinction between mechanics and thermodynamics is worth noting. In mechanics, we solely concentrate on the motion of particles or bodies under the action of forces and torques. On the other hand, thermodynamics is not concerned with the motion of the system as a whole. It is only concerned with the internal macroscopic state of the body.
Thermodynamics Timeline

Different Branches of Thermodynamics
Thermodynamics is classified into the following four branches:
- Classical Thermodynamics
- Statistical Thermodynamics
- Chemical Thermodynamics
- Equilibrium Thermodynamics
Classical Thermodynamics
In classical thermodynamics, the behaviour of matter is analysed with a macroscopic approach. Units such as temperature and pressure are taken into consideration, which helps the individuals calculate other properties and predict the characteristics of the matter undergoing the process.
Statistical Thermodynamics
In statistical thermodynamics, every molecule is under the spotlight, i.e. the properties of every molecule and how they interact are taken into consideration to characterise the behaviour of a group of molecules.
Chemical Thermodynamics
Chemical thermodynamics is the study of how work and heat relate to each other in chemical reactions and in changes of states.
Equilibrium Thermodynamics
Equilibrium thermodynamics is the study of transformations of energy and matter as they approach the state of equilibrium.
Basic Concepts of Thermodynamics – Thermodynamic Terms
Thermodynamics has its own unique vocabulary associated with it. A good understanding of the basic concepts forms a sound understanding of various topics discussed in thermodynamics preventing possible misunderstandings.
Thermodynamic Systems

System
A thermodynamic system is a specific portion of matter with a definite boundary on which our attention is focused. The system boundary may be real or imaginary, fixed or deformable.
There are three types of systems:
- Isolated System – An isolated system cannot exchange energy and mass with its surroundings. The universe is considered an isolated system.
- Closed System – Across the boundary of the closed system, the transfer of energy takes place but the transfer of mass doesn’t take place. Refrigerator, compression of gas in the piston-cylinder assembly are examples of closed systems.
- Open System – In an open system, the mass and energy both may be transferred between the system and surroundings. A steam turbine is an example of an open system.
☓ |
☓ |
☓ |
|
✓ |
✓ |
✓ |
|
☓ |
✓ |
✓ |
|
Surrounding
Everything outside the system that has a direct influence on the behaviour of the system is known as a surrounding.
Thermodynamic Process
A system undergoes a thermodynamic process when there is some energetic change within the system that is associated with changes in pressure, volume and internal energy.
There are four types of thermodynamic processes that have their unique properties, and they are:
- Adiabatic Process – A process where no heat transfer into or out of the system occurs.
- Isochoric Process – A process where no change in volume occurs and the system does no work.
- Isobaric Process – A process in which no change in pressure occurs.
- Isothermal Process – A process in which no change in temperature occurs.
Read More: Thermodynamic Process
A thermodynamic cycle is a process or a combination of processes conducted such that the initial and final states of the system are the same. A thermodynamic cycle is also known as cyclic operation or cyclic processes.
Thermodynamic Equilibrium
At a given state, all properties of a system have fixed values. Thus, if the value of even one property changes, the system’s state changes to a different one. In a system that is in equilibrium, no changes in the value of properties occur when it is isolated from its surroundings.
- When the temperature is the same throughout the entire system, we consider the system to be in thermal equilibrium.
- When there is no change in pressure at any point of the system, we consider the system to be in mechanical equilibrium.
- When the chemical composition of a system does not vary with time, we consider the system to be in chemical equilibrium.
- Phase equilibrium in a two-phase system is when the mass of each phase reaches an equilibrium level.
A thermodynamic system is said to be in thermodynamic equilibrium if it is in chemical equilibrium, mechanical equilibrium and thermal equilibrium and the relevant parameters cease to vary with time.
You may also want to check out these topics given below!
- Kelvin Planck Statement
- Darcy Weisbach Equation Derivation
- Kinetic Theory Of Gases Derivation
- Relation Between Kp And Kc
Thermodynamic Properties
Thermodynamic properties are defined as characteristic features of a system, capable of specifying the system’s state. Thermodynamic properties may be extensive or intensive.
- Intensive properties are properties that do not depend on the quantity of matter. Pressure and temperature are intensive properties.
- In the case of extensive properties, their values depends on the mass of the system. Volume, energy, and enthalpy are extensive properties.
What is Enthalpy?
Enthalpy is the measurement of energy in a thermodynamic system. The quantity of enthalpy equals the total heat content of a system, equivalent to the system’s internal energy plus the product of volume and pressure.
Mathematically, the enthalpy, H, equals the sum of the internal energy, E, and the product of the pressure, P, and volume, V, of the system.
|
What is Entropy?
Entropy is a thermodynamic quantity whose value depends on the physical state or condition of a system. In other words, it is a thermodynamic function used to measure the randomness or disorder.
For example, the entropy of a solid, where the particles are not free to move, is less than the entropy of a gas, where the particles will fill the container.
Thermodynamic Potentials
Thermodynamic potentials are quantitative measures of the stored energy in a system. Potentials measure the energy changes in a system as they evolve from the initial state to the final state. Different potentials are used based on the system constraints, such as temperature and pressure.
Different forms of thermodynamic potentials along with their formula are tabulated below:
| Internal Energy | \(\begin{array}{l}U=\int TdS\;-\;PdV+\sum _{i}\mu _{i}dN_{i}\end{array} \) |
| Helmholtz free energy | F = U – TS |
| Enthalpy | H = U + PV |
| Gibbs Free Energy | G = U + PV – TS |
Thermodynamics Solved Problems
Calculate ΔG at 290 K for the following reaction:
Solution:
Given:
ΔH = -120kJ and ΔS = -150JK-1
To make the unit of ΔS the same as ΔH, we have to convert the unit of ΔS as follows:
We know that,
So,
Therefore, ΔG is -77kJ.
Watch the video to know the top seven JEE Thermodynamics questions.


Laws of Thermodynamics
Thermodynamics laws define the fundamental physical quantities like energy, temperature and entropy that characterize thermodynamic systems at thermal equilibrium. These thermodynamics laws represent how these quantities behave under various circumstances.
How many laws of thermodynamics are there?
There are four laws of thermodynamics and are given below:
- Zeroth law of thermodynamics
- First law of thermodynamics
- Second law of thermodynamics
- Third law of thermodynamics
In the next few sections, we will discuss each of the laws of thermodynamics in detail.
Zeroth Law of Thermodynamics
The Zeroth law of thermodynamics states that if two bodies are individually in equilibrium with a separate third body, then the first two bodies are also in thermal equilibrium with each other.
This means that if system A is in thermal equilibrium with system C and system B is also in equilibrium with system C, then system A and B are also in thermal equilibrium.
An example demonstrating the Zeroth Law
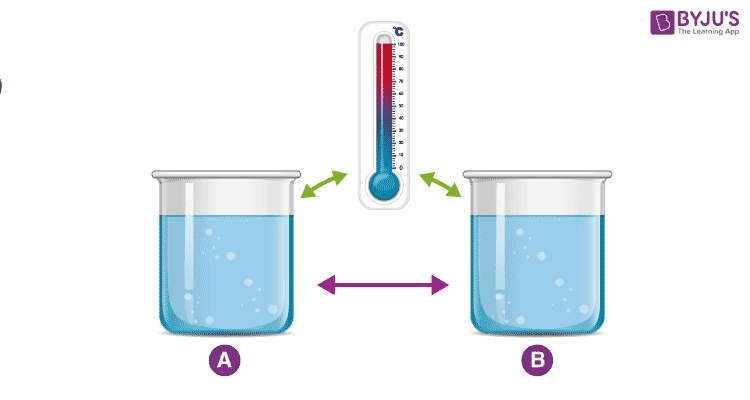
Consider two cups A and B, with boiling water. When a thermometer is placed in cup A, it gets warmed up by the water until it reads 100 °C. When it reads 100 °C, we say that the thermometer is in equilibrium with cup A. When we move the thermometer to cup B to read the temperature, it continues to read 100 °C. The thermometer is also in equilibrium with cup B. By keeping in mind the zeroth law of thermodynamics, we can conclude that cup A and cup B are in equilibrium with each other.
The zeroth law of thermodynamics enables us to use thermometers to compare the temperature of any two objects that we like.
First Law of Thermodynamics
First law of thermodynamics, also known as the law of conservation of energy, states that energy can neither be created nor destroyed, but it can be changed from one form to another.
The first law of thermodynamics may seem abstract, but we will get a clearer idea if we look at a few examples of the first law of thermodynamics.
First Law Of Thermodynamics Examples:
- Plants convert the radiant energy of sunlight to chemical energy through photosynthesis. We eat plants and convert the chemical energy into kinetic energy while we swim, walk, breathe, and scroll through this page.
- Switching on light may seem to produce energy, but it is electrical energy that is converted.
Read More: First Law of Thermodynamics
Second Law of Thermodynamics
Second law of thermodynamics states that the entropy in an isolated system always increases. Any isolated system spontaneously evolves towards thermal equilibrium—the state of maximum entropy of the system.
The entropy of the universe only increases and never decreases. Many individuals take this statement lightly and for granted, but it has an extensive impact and consequence.
Visualizing the second law of thermodynamics
If a room is not tidied or cleaned, it invariably becomes more messy and disorderly with time. When the room is cleaned, its entropy decreases, but the effort to clean it has resulted in increased entropy outside the room exceeding the entropy lost.
Read More: Second Law of Thermodynamics
The video below dives deep into the second law of thermodynamics and will help one take a closer look at how entropy explains disorderliness.

Third Law of Thermodynamics
Third law of thermodynamics states that the entropy of a system approaches a constant value as the temperature approaches absolute zero.
The entropy of a pure crystalline substance (perfect order) at absolute zero temperature is zero. This statement holds true if the perfect crystal has only one state with minimum energy.
Third Law Of Thermodynamics Examples:
Let us consider steam as an example to understand the third law of thermodynamics step by step:
- The molecules within it move freely and have high entropy.
- If one decreases the temperature below 100 °C, the steam gets converted to water, where the movement of molecules is restricted, decreasing the entropy of water.
- When water is further cooled below 0 °C, it gets converted to solid ice. In this state, the movement of molecules is further restricted and the entropy of the system reduces more.
- As the temperature of the ice further reduces, the movement of the molecules in them is restricted further and the entropy of the substance goes on decreasing.
- When the ice is cooled to absolute zero, ideally, the entropy should be zero. But in reality, it is impossible to cool any substance to zero.
Read More:Third Law of Thermodynamics
Thermodynamics Examples in Daily Life
Whether we are sitting in an air-conditioned room or travelling in any vehicle, the application of thermodynamics is everywhere. We have listed a few of these applications below:
- Different types of vehicles such as planes, trucks and ships work on the basis of the 2nd law of thermodynamics.
- The three modes of heat transfer work on the basis of thermodynamics. The heat transfer concepts are widely used in radiators, heaters and coolers.
- Thermodynamics is involved in the study of different types of power plants such as nuclear power plants, thermal power plants.
Thermodynamics – Summary and Overview
→ In simple terms, thermodynamics deals with the transfer of energy from one form to another.
→ The laws of thermodynamics are:
- First law of thermodynamics: Energy can neither be created nor be destroyed, it can only be transferred from one form to another.
- Second law of thermodynamics: The entropy of any isolated system always increases.
- Third law of thermodynamics: The entropy of a system approaches a constant value as the temperature approaches absolute zero.
- Zeroth law of thermodynamics: If two thermodynamic systems are in thermal equilibrium with a third system separately, then they are in thermal equilibrium with each other.
→ Entropy is the measure of the number of possible arrangements the atoms in a system can have.
→ Enthalpy is the measurement of energy in a thermodynamic system.
Frequently Asked Questions – FAQs
What is the importance of the laws of thermodynamics?
What is an example of negative work?
Can energy be destroyed or lost?
Fans convert electrical energy into mechanical energy – this is explained by which law?
Does the human body obey the laws of thermodynamics?
Stay tuned to BYJU’S and Fall in Love with Learning!


Very good explanation
Nicely explained with good videos and examples.
The videos on thermodynamics is very helpful. Thankyou
good explaination sir
Good explanation
Beneficial notes☺