Determinants and matrices, in linear algebra, are used to solve linear equations by applying Cramer’s rule to a set of non-homogeneous equations which are in linear form. Determinants are calculated for square matrices only. If the determinant of a matrix is zero, it is called a singular determinant and if it is one, then it is known as unimodular. For the system of equations to have a unique solution, the determinant of the matrix must be nonsingular, that is its value must be nonzero. In this article, let us discuss the definition of determinants and matrices, different matrices types, properties, with examples.
Table of contents:
- Matrices
- Types of Matrices
- Inverse Matrix
- Transpose of Matrix
- Determinant
- Determinant of a Matrix
- Examples
- FAQs
Matrices Definition
Matrices are the ordered rectangular array of numbers, which are used to express linear equations. A matrix has rows and columns. we can also perform the mathematical operations on matrices such as addition, subtraction, multiplication of matrix. Suppose the number of rows is m and columns is n, then the matrix is represented as m × n matrix.
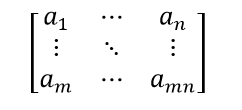
Also, read:
Types of Matrices
There are different types of matrices. Let’s see some of the examples of different types of matrices
- \(\begin{array}{l}\text{Zero Matrix:} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0\\ 0& 0 & 0 \end{bmatrix}\end{array} \)
- \(\begin{array}{l}\text{Identity Matrix: } \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0& 0 & 1 \end{bmatrix}\end{array} \)
- \(\begin{array}{l}\text{Symmetric Matrix: } \begin{bmatrix} 2 & 3 & -1 \\ 3 & 0 & 6\\ -1 & 6 & 5 \end{bmatrix}\end{array} \)
- \(\begin{array}{l}\text{Diagonal Matrix: } \begin{bmatrix} 6 & 0 & 0 \\ 0 & 9 & 0\\ 0 & 0 & 2 \end{bmatrix}\end{array} \)
- \(\begin{array}{l}\text{Upper Triangular Matrix: } \begin{bmatrix} 6 & -1 & 5 \\ 0 & 4 & 2\\ 0 & 0 & 2 \end{bmatrix}\end{array} \)
- \(\begin{array}{l}\text{Lower Triangular Matrix: } \begin{bmatrix} 6 & 0 & 0 \\ 2 & 4 & 0\\ 8 & -1 & 2 \end{bmatrix}\end{array} \)
Inverse of a Matrix
Inverse of a matrix is defined usually for square matrices. For every m × n square matrix, there exists an inverse matrix. If A is the square matrix then A-1 is the inverse of matrix A and satisfies the property:
AA-1 = A-1A = I, where I is the Identity matrix.
Also, the determinant of the square matrix here should not be equal to zero.
Transpose of Matrix
The transpose of a matrix can be determined by rows for the columns. If A is a matrix, then the transpose of a matrix is represented by AT.
For example, let us assume a 3×3 matrix, Say A, then the transpose of A, i.e. AT is given by
In case, if the given square matrix is a symmetric matrix, then the matrix A should be equal to AT.
It means that A = AT.
Definition of Determinant
A determinant can be defined in many ways for a square matrix.
The first and most simple way is to formulate the determinant by taking into account the top row elements and the corresponding minors. Take the first element of the top row and multiply it by it’s minor, then subtract the product of the second element and its minor. Continue to alternately add and subtract the product of each element of the top row with its respective minor until all the elements of the top row have been considered.
For example let us consider a 4×4 matrix A.

Second Method to find the determinant:
The second way to define a determinant is to express in terms of the columns of the matrix by expressing an n x n matrix in terms of the column vectors.
Consider the column vectors of matrix A as A = [ a1, a2, a3, …an] where any element aj is a vector of size x.
Then the determinant of matrix A is defined such that
Det [ a1 + a2 …. baj+cv … ax ] = b det (A) + c det [ a1+ a2 + … v … ax ]
Det [ a1 + a2 …. aj aj+1… ax ] = – det [ a1+ a2 + … aj+1 aj … ax ]
Det (I) = 1
Where the scalars are denoted by b and c, a vector of size x is denoted by v, and the identity matrix of size x is denoted by I.
We can infer from these equations that the determinant is a linear function of the columns. Further, we observe that the sign of the determinant can be interchanged by interchanging the position of adjacent columns. The identity matrix of the respective unit scalar is mapped by the alternating multi-linear function of the columns. This function is the determinant of the matrix.
Check: Determinant Of A 3×3 Matrix
Properties of Determinant
- If In is the identity matrix of the order nxn, then det(I) = 1
- If the matrix MT is the transpose of matrix M, then det (MT) = det (M)
- If matrix M-1 is the inverse of matrix M, then det (M-1) = 1/det (M) = det (M)-1
- If two square matrices M and N have the same size, then det (MN) = det (M) det (N)
- If matrix M has a size axa and C is a constant, then det (CM) = Ca det (M)
- If X, Y, and Z are three positive semidefinite matrices of equal size, then the following holds true along with the corollary det (X+Y) ≥ det(X) + det (Y) for X,Y, Z ≥ 0 det (X+Y+Z) + det C ≥ det (X+Y) + det (Y+Z)
- In a triangular matrix, the determinant is equal to the product of the diagonal elements.
- The determinant of a matrix is zero if all the elements of the matrix are zero.
- Laplace’s Formula and the Adjugate Matrix
Apart from these properties of determinants, there are some other properties, such as
- Reflection Property
- All-zero property
- Proportionality property or Repetition Property
- Switching Property
- Sum Property
- Scalar multiple Property
- Factor Property
- Triangle Property
- Invariance Property
- The determinant of Cofactor matrix
Laplace Formula for Determinant
With Laplace’s formula, the determinant of a matrix can be expressed in terms of the minors of the matrix.
If matrix Bxy is the minor of matrix A obtained by removing xth and yth column and has a size of
( j-1 x j-1), then the determinant of the matrix A is given by
The adjugate matrix is obtained by transposing the matrix containing the cofactors and is given by the equation,
(Adj (A))x,y = (-1)x+y Bx,y
Class Related Links:
Determinant of a Matrix
To solve the system of linear equations and to find the inverse of a matrix, the determinants play an important role. Now, let us discuss how to find the determinant of 2×2 matrix and 3×3 matrix. If A is a matrix, then the determinant of a matrix A is generally represented using det (A) or |A|.
Finding Determinants for 2×2 matrix:
Let us assume a 2×2 square matrix
Finding Determinants for 3×3 Matrix
Now, assume the 3×3 matrix, say
Video Lesson on Matrices and Determinants Class 12


Determinants & It’s Properties

Algebra And Properties Of Matrices

Adjoint and Inverse

System of Equations

Important Conceptual Problems

Characteristic Equation & Polynomial

Determinants and Matrices Solved Examples
Example 1:
Solution:
The determinant of matrix A is
det (A) = |A| = 8 – 6
|A| = 2
Example 2:
Solution:
Therefore,
|A| = 2(35-8) – 3(42-2) +1(24-5)
|A| = 2(27) – 3(40) + 1(19)
|A| = 54-120+19
|A| = 73 -120
Frequently Asked Questions on Determinants and Matrices
Define matrix
A matrix is defined as the rectangular array of numbers. The collection of numbers are arranged in rows and columns
What is meant by determinant?
The determinant is defined as a scalar value which is associated with the square matrix. If X is a matrix, then the determinant of a matrix is represented by |X| or det (X).
Mention the different types of matrices
The different types of matrices are:
Square matrix
Diagonal matrix
Zero matrix
Symmetric matrix
Identity matrix
Upper triangular matrix
Lower Triangular Matrix
Why do we use determinants?
The determinants are used to solve the system of linear equations and it is also used to find the inverse of a matrix.
Mention the important properties of determinants
The properties of determinants are:
Reflection property
Triangle property
All zero property
Sum property
Scalar multiple property
Factor property
Proportionality Property
Download BYJU’S – The Learning App today and learn all about determinants and matrices in a quick and simple way.

it is very useful thankyou byjus team.