Law of cosines signifies the relation between the lengths of sides of a triangle with respect to the cosine of its angle. It is also called the cosine rule. If ABC is a triangle, then as per the statement of cosine law, we have:
a2 = b2 + c2 – 2bc cos α, where a,b, and c are the sides of triangle and α is the angle between sides b and c.
Similarly, if β and γ are the angles between sides ca and ab, respectively, then according to the law of cosine, we have:
b2 = a2 + c2 – 2ac cos β
c2 = b2 + a2 – 2ab cos γ
| Fact: If any one of the angles, α, β or γ is equal to 90 degrees, then the above expression will justify the Pythagoras theorem, because cos 90 = 0. Hence, the above three equations can be expressed as:
a2 = b2 + c2 [if α = 90 degrees] b2 = a2 + c2 [if β = 90 degrees] c2 = b2 + a2 [if γ = 90 degrees] |
Table of Contents:
Law of Cosines Definition
In Trigonometry, the law of Cosines, also known as Cosine Rule or Cosine Formula basically relates the length of the triangle to the cosines of one of its angles. It states that, if the length of two sides and the angle between them is known for a triangle, then we can determine the length of the third side. It is given by:
c2 = a2 + b2 – 2ab cosγ
Where a, b and c are the sides of a triangle and γ is the angle between a and b. See the figure below.
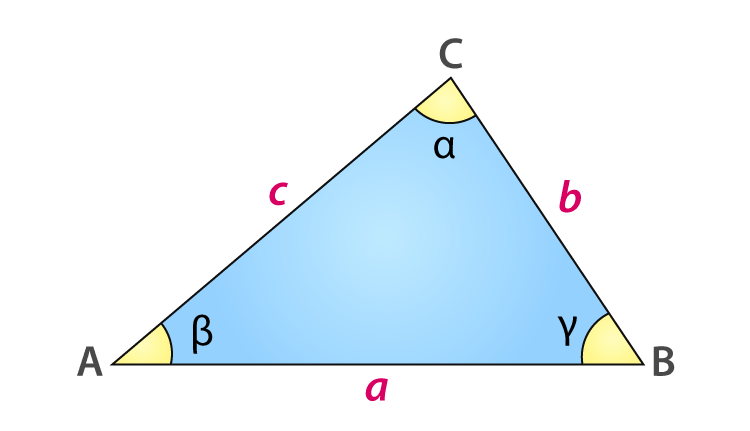
Law of cosines
Formulas
As per the cosines law formula, to find the length of sides of triangle say △ABC, we can write as;
- a2 = b2 + c2 – 2bc cos α
- b2 = a2 + c2 – 2ac cos β
- c2 = b2 + a2 – 2ba cos γ
And if we want to find the angles of △ABC, then the cosine rule is applied as;
- cos α = [b2 + c2 – a2]/2bc
- cos β = [a2 + c2 – b2]/2ac
- cos γ = [b2 + a2 – c2]/2ab
Where a, b and c are the lengths of sides of a triangle.
Solving SSS Congruency
In SSS congruence, we know the lengths of all the three sides of a triangle, and we need to find the measure of the unknown triangle. Therefore, using the law of cosines, we can find the missing angle.
First we need to find one angle using cosine law, say cos α = [b2 + c2 – a2]/2bc.
Then we will find the second angle again using the same law, cos β = [a2 + c2 – b2]/2ac
Now the third angle you can simply find using angle sum property of triangle. That means the sum of all the three angles of a triangle is equal to 180 degrees.
Also Check: Law of cosines calculator
Proof
Now let us learn the law of cosines proof here;
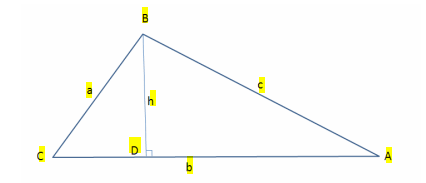
Law of Cosines Proof
In the right triangle BCD, by the definition of cosine function:
cos C = CD/a
or
CD=a cos C
Subtracting above equation from side b, we get
DA = b − acosC ……(1)
In the triangle BCD, according to Sine definition
sin C = BD/a
or
BD = a sinC ……(2)
In the triangle ADB, if we apply the Pythagorean Theorem, then
c2 = BD2 + DA2
Substituting for BD and DA from equations (1) and (2)
c2 = (a sin C)2 + (b-acosC)2
By Cross Multiplication we get:
c2 = a2 sin2C + b2 – 2abcosC + a2 cos2C
Rearranging the above equation:
c2 = a2 sin2C + a2 cos2C + b2 – 2ab cosC
Taking out a2 as a common factor, we get;
c2 = a2(sin2C + cos2C) + b2 – 2ab cosC
Now from the above equation, you know that,
sin2θ + cos2θ = 1
∴ c2 = a2 + b2 – 2ab cosC
Hence, the cosine law is proved.
Also read:
Problem and Solution
Let us understand the concept by solving one of the cosines law problems.
Problem: A triangle ABC has sides a=10cm, b=7cm and c=5cm. Now, find its angle ‘x’.
Solution:
Consider the below triangle as triangle ABC, where,
a=10cm
b=7cm
c=5cm
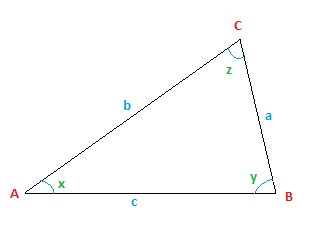
Law of Cosine Problems
By using cosines law,
a2 = b2 + c2 – 2bc cos(x)
Or
cos x = (b2 + c2 – a2)/2bc
Substituting the value of the sides of the triangle i.e a,b and c, we get
cos(x) = (72 + 52 – 102)/(2 × 7 × 5)
cos(x)=(49 + 25 -100)/70
cos(x)= -0.37
It is important to solve more problems based on cosines law formula by changing the values of sides a, b & c and cross-check law of cosines calculator given above.
Frequently Asked Questions – FAQs
What is law of cosine?
What does the cosine law states?
a2 = b2 + c2 – 2bc cos α
b2 = a2 + c2 – 2ac cos β
c2 = b2 + a2 – 2ba cos γ
where a,b, and c are the sides of the triangle.
When should we use the law of cosines?
Can we use cosine law for all the triangles?
How to solve the law of cosines?
a2 = b2 + c2 -2bc cos α
Where a is the unknown side, b and c are the known sides of the triangle, and α is the angle between b and c.
What is the formula to find the angle using cosine law?
cos α = [b2 + c2 – a2]/2bc
cos β = [a2 + c2 – b2]/2ac
cos γ = [b2 + a2 – c2]/2ab


Comments