NCERT Solutions Class 10 Maths Chapter 4 – CBSE Free PDF Download
NCERT Solutions Class 10 Maths Chapter 4 Quadratic Equations contain all the solutions to the problems provided in the Class 10 Maths NCERT textbook for CBSE exam preparations. The questions from every section are framed and solved accurately by the subject experts. NCERT Solutions for Class 10 are detailed and step-by-step guides to all the queries of the students. The exercises present in the chapter should be dealt with utmost sincerity if one wants to score well in the examinations. Maths is a subject that requires a good understanding and a lot of practice. The tips and tricks to solve the problems easily are also provided here. A quadratic equation in the variable x is an equation of the form ax2+ bx + c = 0, where a, b, c are real numbers, a ≠ 0. That is, ax2+ bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.
Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 4 Quadratic Equations
Download Most Important Questions for Class 10 Maths Chapter – 4 Quadratic Equations
Quadratic equations arise in several situations around us. Hence, students should give special attention to learning the concepts related to this chapter of the latest CBSE Syllabus for 2023-24 thoroughly to excel in Class 10 Maths examinations. NCERT Solutions help the students in learning these concepts as well as in evaluating themselves. Practising these solutions repeatedly is bound to help the students in overcoming their shortcomings. Maths has either a correct answer or a wrong one. Therefore, it is imperative to concentrate while solving the questions to score full marks.
NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations
Access answers to NCERT Class 10 Maths Chapter 4 – Quadratic Equations
Exercise 4.1 Page: 73
1. Check whether the following are quadratic equations:
(i) (x + 1)2 = 2(x – 3)
(ii) x2 – 2x = (–2) (3 – x)
(iii) (x – 2)(x + 1) = (x – 1)(x + 3)
(iv) (x – 3)(2x +1) = x(x + 5)
(v) (2x – 1)(x – 3) = (x + 5)(x – 1)
(vi) x2 + 3x + 1 = (x – 2)2
(vii) (x + 2)3 = 2x (x2 – 1)
(viii) x3 – 4x2 – x + 1 = (x – 2)3
Solutions:
(i) Given,
(x + 1)2 = 2(x – 3)
By using the formula for (a+b)2 = a2+2ab+b2
⇒ x2 + 2x + 1 = 2x – 6
⇒ x2 + 7 = 0
The above equation is in the form of ax2 + bx + c = 0
Therefore, the given equation is a quadratic equation.
(ii) Given, x2 – 2x = (–2) (3 – x)
⇒ x2 – 2x = -6 + 2x
⇒ x2 – 4x + 6 = 0
The above equation is in the form of ax2 + bx + c = 0
Therefore, the given equation is a quadratic equation.
(iii) Given, (x – 2)(x + 1) = (x – 1)(x + 3)
By multiplication,
⇒ x2 – x – 2 = x2 + 2x – 3
⇒ 3x – 1 = 0
The above equation is not in the form of ax2 + bx + c = 0
Therefore, the given equation is not a quadratic equation.

(iv) Given, (x – 3)(2x +1) = x(x + 5)
By multiplication,
⇒ 2x2 – 5x – 3 = x2 + 5x
⇒ x2 – 10x – 3 = 0
The above equation is in the form of ax2 + bx + c = 0
Therefore, the given equation is a quadratic equation.

(v) Given, (2x – 1)(x – 3) = (x + 5)(x – 1)
By multiplication,
⇒ 2x2 – 7x + 3 = x2 + 4x – 5
⇒ x2 – 11x + 8 = 0
The above equation is in the form of ax2 + bx + c = 0.
Therefore, the given equation is a quadratic equation.
(vi) Given, x2 + 3x + 1 = (x – 2)2
By using the formula for (a-b)2=a2-2ab+b2
⇒ x2 + 3x + 1 = x2 + 4 – 4x
⇒ 7x – 3 = 0
The above equation is not in the form of ax2 + bx + c = 0
Therefore, the given equation is not a quadratic equation.

(vii) Given, (x + 2)3 = 2x(x2 – 1)
By using the formula for (a+b)3 = a3+b3+3ab(a+b)
⇒ x3 + 8 + x2 + 12x = 2x3 – 2x
⇒ x3 + 14x – 6x2 – 8 = 0
The above equation is not in the form of ax2 + bx + c = 0
Therefore, the given equation is not a quadratic equation.
(viii) Given, x3 – 4x2 – x + 1 = (x – 2)3
By using the formula for (a-b)3 = a3-b3-3ab(a-b)
⇒ x3 – 4x2 – x + 1 = x3 – 8 – 6x2 + 12x
⇒ 2x2 – 13x + 9 = 0
The above equation is in the form of ax2 + bx + c = 0
Therefore, the given equation is a quadratic equation.
2. Represent the following situations in the form of quadratic equations:
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken
Solutions:
(i) Let us consider,
The breadth of the rectangular plot = x m
Thus, the length of the plot = (2x + 1) m
As we know,
Area of rectangle = length × breadth = 528 m2
Putting the value of the length and breadth of the plot in the formula, we get,
(2x + 1) × x = 528
⇒ 2x2 + x =528
⇒ 2x2 + x – 528 = 0
Therefore, the length and breadth of the plot satisfy the quadratic equation, 2x2 + x – 528 = 0, which is the required representation of the problem mathematically.

(ii) Let us consider,
The first integer number = x
Thus, the next consecutive positive integer will be = x + 1
Product of two consecutive integers = x × (x +1) = 306
⇒ x2 + x = 306
⇒ x2 + x – 306 = 0
Therefore, the two integers x and x+1 satisfy the quadratic equation, x2 + x – 306 = 0, which is the required representation of the problem mathematically.
(iii) Let us consider,
Age of Rohan’s = x years
Therefore, as per the given question,
Rohan’s mother’s age = x + 26
After 3 years,
Age of Rohan’s = x + 3
Age of Rohan’s mother will be = x + 26 + 3 = x + 29
The product of their ages after 3 years will be equal to 360, such that
(x + 3)(x + 29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 32x + 87 – 360 = 0
⇒ x2 + 32x – 273 = 0
Therefore, the age of Rohan and his mother satisfies the quadratic equation, x2 + 32x – 273 = 0, which is the required representation of the problem mathematically.

(iv) Let us consider,
The speed of the train = x km/h
And
Time taken to travel 480 km = 480/x km/hr
As per second condition, the speed of train = (x – 8) km/h
Also given, the train will take 3 hours to cover the same distance.
Therefore, time taken to travel 480 km = (480/x)+3 km/h
As we know,
Speed × Time = Distance
Therefore,
(x – 8)(480/x )+ 3 = 480
⇒ 480 + 3x – 3840/x – 24 = 480
⇒ 3x – 3840/x = 24
⇒ x2 – 8x – 1280 = 0
Therefore, the speed of the train satisfies the quadratic equation, x2 – 8x – 1280 = 0, which is the required representation of the problem mathematically.

Exercise 4.2 Page: 76
1. Find the roots of the following quadratic equations by factorisation:
(i) x2 – 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) √2 x2 + 7x + 5√2 = 0
(iv) 2x2 – x +1/8 = 0
(v) 100x2 – 20x + 1 = 0
Solutions:
(i) Given, x2 – 3x – 10 =0
Taking L.H.S.,
=>x2 – 5x + 2x – 10
=>x(x – 5) + 2(x – 5)
=>(x – 5)(x + 2)
The roots of this equation, x2 – 3x – 10 = 0 are the values of x for which (x – 5)(x + 2) = 0
Therefore, x – 5 = 0 or x + 2 = 0
=> x = 5 or x = -2
(ii) Given, 2x2 + x – 6 = 0
Taking L.H.S.,
=> 2x2 + 4x – 3x – 6
=> 2x(x + 2) – 3(x + 2)
=> (x + 2)(2x – 3)
The roots of this equation, 2x2 + x – 6=0 are the values of x for which (x x + 2)(2x – 3) = 0
Therefore, x + 2 = 0 or 2x – 3 = 0
=> x = -2 or x = 3/2
(iii) √2 x2 + 7x + 5√2=0
Taking L.H.S.,
=> √2 x2 + 5x + 2x + 5√2
=> x (√2x + 5) + √2(√2x + 5)= (√2x + 5)(x + √2)
The roots of this equation, √2 x2 + 7x + 5√2=0 are the values of x for which (√2x + 5)(x + √2) = 0
Therefore, √2x + 5 = 0 or x + √2 = 0
=> x = -5/√2 or x = -√2
(iv) 2x2 – x +1/8 = 0
Taking L.H.S.,
=1/8 (16x2 – 8x + 1)
= 1/8 (16x2 – 4x -4x + 1)
= 1/8 (4x(4x – 1) -1(4x – 1))
= 1/8 (4x – 1)2
The roots of this equation, 2x2 – x + 1/8 = 0, are the values of x for which (4x – 1)2= 0
Therefore, (4x – 1) = 0 or (4x – 1) = 0
⇒ x = 1/4 or x = 1/4
(v) Given, 100x2 – 20x + 1=0
Taking L.H.S.,
= 100x2 – 10x – 10x + 1
= 10x(10x – 1) -1(10x – 1)
= (10x – 1)2
The roots of this equation, 100x2 – 20x + 1=0, are the values of x for which (10x – 1)2= 0
∴ (10x – 1) = 0 or (10x – 1) = 0
⇒x = 1/10 or x = 1/10
2. Solve the problems given in Example 1.
Represent the following situations mathematically:
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was Rs. 750. We would like to find out the number of toys produced on that day.
Solutions:
(i) Let us say the number of marbles John has = x
Therefore, the number of marble Jivanti has = 45 – x
After losing 5 marbles each,
Number of marbles John has = x – 5
Number of marble Jivanti has = 45 – x – 5 = 40 – x
Given that the product of their marbles is 124.
∴ (x – 5)(40 – x) = 124
⇒ x2 – 45x + 324 = 0
⇒ x2 – 36x – 9x + 324 = 0
⇒ x(x – 36) -9(x – 36) = 0
⇒ (x – 36)(x – 9) = 0
Thus, we can say,
x – 36 = 0 or x – 9 = 0
⇒ x = 36 or x = 9
Therefore,
If John’s marbles = 36
Then, Jivanti’s marbles = 45 – 36 = 9
And if John’s marbles = 9
Then, Jivanti’s marbles = 45 – 9 = 36
(ii) Let us say the number of toys produced in a day is x.
Therefore, cost of production of each toy = Rs(55 – x)
Given the total cost of production of the toys = Rs 750
∴ x(55 – x) = 750
⇒ x2 – 55x + 750 = 0
⇒ x2 – 25x – 30x + 750 = 0
⇒ x(x – 25) -30(x – 25) = 0
⇒ (x – 25)(x – 30) = 0
Thus, either x -25 = 0 or x – 30 = 0
⇒ x = 25 or x = 30
Hence, the number of toys produced in a day will be either 25 or 30.
3. Find two numbers whose sum is 27 and product is 182.
Solution:
Let us say the first number is x, and the second number is 27 – x.
Therefore, the product of two numbers
x(27 – x) = 182
⇒ x2 – 27x – 182 = 0
⇒ x2 – 13x – 14x + 182 = 0
⇒ x(x – 13) -14(x – 13) = 0
⇒ (x – 13)(x -14) = 0
Thus, either, x = -13 = 0 or x – 14 = 0
⇒ x = 13 or x = 14
Therefore, if first number = 13, then second number = 27 – 13 = 14
And if first number = 14, then second number = 27 – 14 = 13
Hence, the numbers are 13 and 14.
4. Find two consecutive positive integers, the sum of whose squares is 365.
Solution:
Let us say the two consecutive positive integers are x and x + 1.
Therefore, as per the given questions,
x2 + (x + 1)2 = 365
⇒ x2 + x2 + 1 + 2x = 365
⇒ 2x2 + 2x – 364 = 0
⇒ x2 + x – 182 = 0
⇒ x2 + 14x – 13x – 182 = 0
⇒ x(x + 14) -13(x + 14) = 0
⇒ (x + 14)(x – 13) = 0
Thus, either, x + 14 = 0 or x – 13 = 0,
⇒ x = – 14 or x = 13
Since the integers are positive, x can be 13 only.
∴ x + 1 = 13 + 1 = 14
Therefore, two consecutive positive integers will be 13 and 14.
5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let us say the base of the right triangle is x cm.
Given, the altitude of right triangle = (x – 7) cm
From Pythagoras’ theorem, we know,
Base2 + Altitude2 = Hypotenuse2
∴ x2 + (x – 7)2 = 132
⇒ x2 + x2 + 49 – 14x = 169
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
Thus, either x – 12 = 0 or x + 5 = 0,
⇒ x = 12 or x = – 5
Since sides cannot be negative, x can only be 12.
Therefore, the base of the given triangle is 12 cm, and the altitude of this triangle will be (12 – 7) cm = 5 cm.
6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs.90, find the number of articles produced and the cost of each article.
Solution:
Let us say the number of articles produced is x.
Therefore, cost of production of each article = Rs (2x + 3)
Given the total cost of production is Rs.90
∴ x(2x + 3) = 90
⇒ 2x2 + 3x – 90 = 0
⇒ 2x2 + 15x -12x – 90 = 0
⇒ x(2x + 15) -6(2x + 15) = 0
⇒ (2x + 15)(x – 6) = 0
Thus, either 2x + 15 = 0 or x – 6 = 0
⇒ x = -15/2 or x = 6
As the number of articles produced can only be a positive integer, x can only be 6.
Hence, the number of articles produced = 6
Cost of each article = 2 × 6 + 3 = Rs 15
Exercise 4.3 Page: 87
1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x +3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solutions:
(i) 2x2 – 7x + 3 = 0
⇒ 2x2 – 7x = – 3
Dividing by 2 on both sides, we get
⇒ x2 -7x/2 = -3/2
⇒ x2 -2 × x ×7/4 = -3/2
On adding (7/4)2 to both sides of the equation, we get
⇒ (x)2-2×x×7/4 +(7/4)2 = (7/4)2-3/2
⇒ (x-7/4)2 = (49/16) – (3/2)
⇒(x-7/4)2 = 25/16
⇒(x-7/4)2 = ±5/4
⇒ x = 7/4 ± 5/4
⇒ x = 7/4 + 5/4 or x = 7/4 – 5/4
⇒ x = 12/4 or x = 2/4
⇒ x = 3 or x = 1/2
(ii) 2x2 + x – 4 = 0
⇒ 2x2 + x = 4
Dividing both sides of the equation by 2, we get
⇒ x2 +x/2 = 2
Now on adding (1/4)2 to both sides of the equation, we get,
⇒ (x)2 + 2 × x × 1/4 + (1/4)2 = 2 + (1/4)2
⇒ (x + 1/4)2 = 33/16
⇒ x + 1/4 = ± √33/4
⇒ x = ± √33/4 – 1/4
⇒ x = (± √33-1)/4
Therefore, either x = (√33-1)/4 or x = (-√33-1)/4
(iii) 4x2 + 4√3x + 3 = 0
Converting the equation into a2+2ab+b2 form, we get,
⇒ (2x)2 + 2 × 2x × √3 + (√3)2 = 0
⇒ (2x + √3)2 = 0
⇒ (2x + √3) = 0 and (2x + √3) = 0
Therefore, either x = -√3/2 or x = -√3/2
(iv) 2x2 + x + 4 = 0
⇒ 2x2 + x = -4
Dividing both sides of the equation by 2, we get
⇒ x2 + 1/2x = 2
⇒ x2 + 2 × x × 1/4 = -2
By adding (1/4)2 to both sides of the equation, we get
⇒ (x)2 + 2 × x × 1/4 + (1/4)2 = (1/4)2 – 2
⇒ (x + 1/4)2 = 1/16 – 2
⇒ (x + 1/4)2 = -31/16
As we know, the square of numbers cannot be negative.
Therefore, there is no real root for the given equation, 2x2 + x + 4 = 0
2. Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.
(i) 2x2 – 7x + 3 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = -7 and c = 3
By using the quadratic formula, we get,
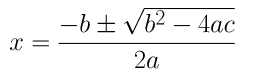
⇒ x = (7±√(49 – 24))/4
⇒ x = (7±√25)/4
⇒ x = (7±5)/4
⇒ x = (7+5)/4 or x = (7-5)/4
⇒ x = 12/4 or 2/4
∴ x = 3 or 1/2
(ii) 2x2 + x – 4 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = -4
By using the quadratic formula, we get,
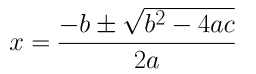
⇒x = (-1±√1+32)/4
⇒x = (-1±√33)/4
∴ x = (-1+√33)/4 or x = (-1-√33)/4
(iii) 4x2 + 4√3x + 3 = 0
On comparing the given equation with ax2 + bx + c = 0, we get
a = 4, b = 4√3 and c = 3
By using the quadratic formula, we get,
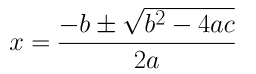
⇒ x = (-4√3±√48-48)/8
⇒ x = (-4√3±0)/8
∴ x = -√3/2 or x = -√3/2
(iv) 2x2 + x + 4 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = 4
By using the quadratic formula, we get
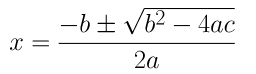
⇒ x = (-1±√1-32)/4
⇒ x = (-1±√-31)/4
As we know, the square of a number can never be negative. Therefore, there is no real solution for the given equation.
3. Find the roots of the following equations:
(i) x-1/x = 3, x ≠ 0
(ii) 1/x+4 – 1/x-7 = 11/30, x = -4, 7
Solution:
(i) x-1/x = 3
⇒ x2 – 3x -1 = 0
On comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = -3 and c = -1
By using the quadratic formula, we get,
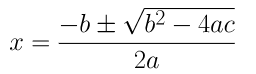
⇒ x = (3±√9+4)/2
⇒ x = (3±√13)/2
∴ x = (3+√13)/2 or x = (3-√13)/2
(ii) 1/x+4 – 1/x-7 = 11/30
⇒ x-7-x-4/(x+4)(x-7) = 11/30
⇒ -11/(x+4)(x-7) = 11/30
⇒ (x+4)(x-7) = -30
⇒ x2 – 3x – 28 = 30
⇒ x2 – 3x + 2 = 0
We can solve this equation by factorisation method now.
⇒ x2 – 2x – x + 2 = 0
⇒ x(x – 2) – 1(x – 2) = 0
⇒ (x – 2)(x – 1) = 0
⇒ x = 1 or 2
4. The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
Solution:
Let us say the present age of Rahman is x years.
Three years ago, Rehman’s age was (x – 3) years.
Five years after, his age will be (x + 5) years.
Given the sum of the reciprocals of Rehman’s ages 3 years ago and after 5 years is equal to 1/3.
∴ 1/x-3 + 1/x-5 = 1/3
(x+5+x-3)/(x-3)(x+5) = 1/3
(2x+2)/(x-3)(x+5) = 1/3
⇒ 3(2x + 2) = (x-3)(x+5)
⇒ 6x + 6 = x2 + 2x – 15
⇒ x2 – 4x – 21 = 0
⇒ x2 – 7x + 3x – 21 = 0
⇒ x(x – 7) + 3(x – 7) = 0
⇒ (x – 7)(x + 3) = 0
⇒ x = 7, -3
As we know, age cannot be negative.
Therefore, Rahman’s present age is 7 years.
5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution:
Let us say the marks of Shefali in Maths be x.
Then, the marks in English will be 30 – x.
As per the given question,
(x + 2)(30 – x – 3) = 210
(x + 2)(27 – x) = 210
⇒ -x2 + 25x + 54 = 210
⇒ x2 – 25x + 156 = 0
⇒ x2 – 12x – 13x + 156 = 0
⇒ x(x – 12) -13(x – 12) = 0
⇒ (x – 12)(x – 13) = 0
⇒ x = 12, 13
Therefore, if the marks in Maths are 12, then marks in English will be 30 – 12 = 18, and if the marks in Maths are 13, then marks in English will be 30 – 13 = 17.
6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let us say the shorter side of the rectangle is x m.
Then, larger side of the rectangle = (x + 30) m
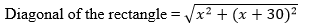
As given, the length of the diagonal is = x + 30 m
Therefore,
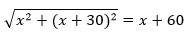
⇒ x2 + (x + 30)2 = (x + 60)2
⇒ x2 + x2 + 900 + 60x = x2 + 3600 + 120x
⇒ x2 – 60x – 2700 = 0
⇒ x2 – 90x + 30x – 2700 = 0
⇒ x(x – 90) + 30(x -90) = 0
⇒ (x – 90)(x + 30) = 0
⇒ x = 90, -30
However, the side of the field cannot be negative. Therefore, the length of the shorter side will be 90 m.
And the length of the larger side will be (90 + 30) m = 120 m.
7. The difference of the squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let us say the larger and smaller number be x and y, respectively.
As per the question given,
x2 – y2 = 180 and y2 = 8x
⇒ x2 – 8x = 180
⇒ x2 – 8x – 180 = 0
⇒ x2 – 18x + 10x – 180 = 0
⇒ x(x – 18) +10(x – 18) = 0
⇒ (x – 18)(x + 10) = 0
⇒ x = 18, -10
However, the larger number cannot be considered a negative number, as 8 times the larger number will be negative, and hence, the square of the smaller number will be negative, which is not possible.
Therefore, the larger number will be 18 only.
x = 18
∴ y2 = 8x = 8 × 18 = 144
⇒ y = ±√144 = ±12
∴ Smaller number = ±12
Therefore, the numbers are 18 and 12 or 18 and -12.
8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
It is given that
Distance = 360 km
Consider x as the speed, then the time taken
t = 360/x
If the speed is increased by 5 km/h, the speed will be (x + 5) km/h.
Distance will be the same.
t = 360/(x + 5)
We know that
Time with original speed – Time with increased speed = 1
360/x – 360/(x + 5) = 1
LCM = x (x + 5)
[360 (x + 5) – 360x]/x(x + 5) = 1360 x + 1800 – 360x = x (x + 5)
x2 + 5x = 1800
x2 + 5x – 1800 = 0
x2 + 45x – 40x – 1800 = 0
x (x + 45) – 40 (x + 45) = 0
(x – 40) (x + 45) = 0
x = 40 km/hr
As we know, the value of speed cannot be negative.
Therefore, the speed of the train is 40 km/h.
9. Two water taps together can fill a tank in
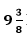 hours. The tap of a larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time at which each tap can separately fill the tank.
hours. The tap of a larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time at which each tap can separately fill the tank.
Solution:
Let the time taken by the smaller pipe to fill the tank = x hr.
Time taken by the larger pipe = (x – 10) hr
Part of the tank filled by smaller pipe in 1 hour = 1/x
Part of the tank filled by larger pipe in 1 hour = 1/(x – 10)
As given, the tank can be filled in
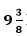 = 75/8 hours by both the pipes together.
= 75/8 hours by both the pipes together.
Therefore,
1/x + 1/x-10 = 8/75
x-10+x/x(x-10) = 8/75
⇒ 2x-10/x(x-10) = 8/75
⇒ 75(2x – 10) = 8x2 – 80x
⇒ 150x – 750 = 8x2 – 80x
⇒ 8x2 – 230x +750 = 0
⇒ 8x2 – 200x – 30x + 750 = 0
⇒ 8x(x – 25) -30(x – 25) = 0
⇒ (x – 25)(8x -30) = 0
⇒ x = 25, 30/8
Time taken by the smaller pipe cannot be 30/8 = 3.75 hours, as the time taken by the larger pipe will become negative, which is logically not possible.
Therefore, the time taken individually by the smaller pipe and the larger pipe will be 25 and 25 – 10 =15 hours, respectively.
10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let us say the average speed of the passenger train = x km/h.
Average speed of express train = (x + 11) km/h
Given the time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance. Therefore,
(132/x) – (132/(x+11)) = 1
132(x+11-x)/(x(x+11)) = 1
132 × 11 /(x(x+11)) = 1
⇒ 132 × 11 = x(x + 11)
⇒ x2 + 11x – 1452 = 0
⇒ x2 + 44x -33x -1452 = 0
⇒ x(x + 44) -33(x + 44) = 0
⇒ (x + 44)(x – 33) = 0
⇒ x = – 44, 33
As we know, speed cannot be negative.
Therefore, the speed of the passenger train will be 33 km/h and thus, the speed of the express train will be 33 + 11 = 44 km/h.
11. Sum of the areas of two squares is 468 m2. If the difference between their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the sides of the two squares be x m and y m.
Therefore, their perimeter will be 4x and 4y, respectively
And the area of the squares will be x2 and y2, respectively.
Given,
4x – 4y = 24
x – y = 6
x = y + 6
Also, x2 + y2 = 468
⇒ (6 + y2) + y2 = 468
⇒ 36 + y2 + 12y + y2 = 468
⇒ 2y2 + 12y + 432 = 0
⇒ y2 + 6y – 216 = 0
⇒ y2 + 18y – 12y – 216 = 0
⇒ y(y +18) -12(y + 18) = 0
⇒ (y + 18)(y – 12) = 0
⇒ y = -18, 12
As we know, the side of a square cannot be negative.
Hence, the sides of the squares are 12 m and (12 + 6) m = 18 m.
Exercise 4.4 Page: 91
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them.
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
Solutions:
(i) Given,
2x2 – 3x + 5 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -3 and c = 5
We know, Discriminant = b2 – 4ac
= ( – 3)2 – 4 (2) (5) = 9 – 40
= – 31
As you can see, b2 – 4ac < 0
Therefore, no real root is possible for the given equation, 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = -4√3 and c = 4
We know, Discriminant = b2 – 4ac
= (-4√3)2 – 4(3)(4)
= 48 – 48 = 0
As b2 – 4ac = 0,
Real roots exist for the given equation, and they are equal to each other.
Hence, the roots will be –b/2a and –b/2a.
–b/2a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
(iii) 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -6, c = 3
As we know, Discriminant = b2 – 4ac
= (-6)2 – 4 (2) (3)
= 36 – 24 = 12
As b2 – 4ac > 0,
Therefore, there are distinct real roots that exist for this equation, 2x2 – 6x + 3 = 0
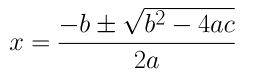
= (-(-6) ± √(-62-4(2)(3)) )/ 2(2)
= (6±2√3 )/4
= (3±√3)/2
Therefore, the roots for the given equation are (3+√3)/2 and (3-√3)/2
2. Find the values of k for each of the following quadratic equations so that they have two equal roots.
(i) 2x2 + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solutions:
(i) 2x2 + kx + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = k and c = 3
As we know, Discriminant = b2 – 4ac
= (k)2 – 4(2) (3)
= k2 – 24
For equal roots, we know,
Discriminant = 0
k2 – 24 = 0
k2 = 24
k = ±√24 = ±2√6
(ii) kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = k, b = – 2k and c = 6
We know, Discriminant = b2 – 4ac
= ( – 2k)2 – 4 (k) (6)
= 4k2 – 24k
For equal roots, we know,
b2 – 4ac = 0
4k2 – 24k = 0
4k (k – 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x2‘ and ‘x‘.
Therefore, if this equation has two equal roots, k should be 6 only.
3. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2? If so, find its length and breadth.
Solution:
Let the breadth of the mango grove be l.
The length of the mango grove will be 2l.
Area of the mango grove = (2l) (l)= 2l2
2l2 = 800
l2 = 800/2 = 400
l2 – 400 =0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = 0, c = 400
As we know, Discriminant = b2 – 4ac
=> (0)2 – 4 × (1) × ( – 400) = 1600
Here, b2 – 4ac > 0
Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ±20
As we know, the value of length cannot be negative.
Therefore, the breadth of the mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m
4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their age in years was 48.
Solution:
Let’s say the age of one friend is x years.
Then, the age of the other friend will be (20 – x) years.
Four years ago,
Age of First friend = (x – 4) years
Age of Second friend = (20 – x – 4) = (16 – x) years
As per the given question, we can write,
(x – 4) (16 – x) = 48
16x – x2 – 64 + 4x = 48
– x2 + 20x – 112 = 0
x2 – 20x + 112 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -20 and c = 112
Discriminant = b2 – 4ac
= (-20)2 – 4 × 112
= 400 – 448 = -48
b2 – 4ac < 0
Therefore, there will be no real solution possible for the equations. Hence, the condition doesn’t exist.
5. Is it possible to design a rectangular park of perimeter 80 and an area of 400 m2? If so, find its length and breadth.
Solution:
Let the length and breadth of the park be l and b.
Perimeter of the rectangular park = 2 (l + b) = 80
So, l + b = 40
Or, b = 40 – l
Area of the rectangular park = l×b = l(40 – l) = 40l – l2 = 400
l2 – 40l + 400 = 0, which is a quadratic equation.
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -40, c = 400
Since, Discriminant = b2 – 4ac
=(-40)2 – 4 × 400
= 1600 – 1600 = 0
Thus, b2 – 4ac = 0
Therefore, this equation has equal real roots. Hence, the situation is possible.
The root of the equation,
l = –b/2a
l = -(-40)/2(1) = 40/2 = 20
Therefore, the length of the rectangular park, l = 20 m
And the breadth of the park, b = 40 – l = 40 – 20 = 20 m.
| Also Access |
| NCERT Exemplar for Class 10 Maths Chapter 4 |
| CBSE Notes for Class 10 Maths Chapter 4 |
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations
A 1-mark question was asked from Chapter 4 Quadratic Equations in the year 2018. However, in the year 2017, a total of 13 marks were asked from the topic Quadratic Equations. Therefore, students need to have a thorough understanding of the topic. The topics and sub-topics provided in this chapter include:
4.1 Introduction
If we equate the polynomial ax2+ bx + c, a ≠ 0 to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations. In this chapter, students will study quadratic equations and various ways of finding their roots. They will also see some applications of quadratic equations in daily life situations.
4.2 Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax2+ bx + c = 0, where a, b, c are real numbers, a ≠ 0. In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation. But when we write the terms of p(x) in descending order of their degrees, then we get the standard form of the equation. That is, ax2+ bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.
4.3 Solution of Quadratic Equations by Factorisation
A real number α is called a root of the quadratic equation ax2 + bx + c = 0, a ≠ 0 if a α2+ bα + c = 0. We also say that x = α is a solution of the quadratic equation or that α satisfies the quadratic equation. Note that the zeroes of the quadratic polynomial ax2+ bx + c and the roots of the quadratic equation ax2 + bx + c = 0 are the same.
4.4 Solution of a Quadratic Equation by Completing the Square
Finding the value that makes a quadratic equation a square trinomial is called completing the square. The square trinomial can then be solved easily by factorising.
4.5 Nature of Roots
If b2 – 4ac < 0, then there is no real number whose square is b2 – 4ac. Therefore, there are no real roots for the given quadratic equation in this case. Since b2 – 4ac determines whether the quadratic equation ax2 + bx + c = 0 has real roots or not, b2 – 4ac is called the discriminant of this quadratic equation. So, a quadratic equation ax2 + bx + c = 0 has (i) two distinct real roots, if b2 – 4ac > 0, (ii) two equal real roots, if b2– 4ac = 0, (iii) no real roots, if b2– 4ac < 0. 4.6
Summary
List of exercises we covered in NCERT Solutions for Class 10 Maths Chapter 4
Exercise 4.1 Solutions– 2 Questions
Exercise 4.2 Solutions– 6 Questions
Exercise 4.3 Solutions– 11 Questions
Exercise 4.4 Solutions– 5 Questions
In a quadratic equation, x represents an unknown form, and a, b, and c are the known values. An equation to be quadratic “a” should not be equal to 0. The equation is of the form ax2 + bx + c = 0. The values of a, b, and c are always real numbers. A quadratic equation can be calculated by completing the square. A quadratic equation has
- Two different real roots
- No real roots
- Two equal roots
Key Features of NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations
- The highly experienced faculty at BYJU’S designs NCERT Solutions with utmost care.
- The solutions are 100% accurate and can be used by the students while preparing for their CBSE board exams.
- All the minute concepts are also covered to help students face other competitive exams more confidently.
- The exercise questions present in the NCERT Textbook have been answered in a step-wise manner so that students attain good scores not only on the final answer but also on each step.
For more questions to practise, students can refer to the other study materials which are given at BYJU’S.
Disclaimer –
Dropped Topics – 4.4 Solution of a quadratic equation by completing the squares



























It is good learning app
It is good learning app