NCERT Solutions is the best guide for students with detailed study material, including important topics. NCERT Solutions for Class 10 Chapter 4 – Quadratic Equations is an important chapter, and the students are advised to study it carefully. NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.4 contains solutions to all the questions mentioned on page number 91 in the textbook.
Mathematics is one subject that requires a lot of practice. Stepwise solutions to the questions are provided on this page for better practice. The solutions are provided by the subject experts and are beneficial in scoring good marks in the examinations. Students should go through the questions provided in NCERT Solutions Class 10 Maths after completing each chapter. This helps to analyse their shortcomings and study accordingly.
NCERT Solutions are very helpful from the examination perspective. The subject experts have tried to include all topics and concepts that are important. Students can refer to the NCERT Class 10 solutions for a better understanding of the topics. Students appearing for the board examinations will find it helpful to prepare for the examinations.
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.4
Access Other Exercise Solutions of Class 10 Maths Chapter 4 – Quadratic Equations
Exercise 4.1 Solutions– 2 Questions
Exercise 4.2 Solutions– 6 Questions
Exercise 4.3 Solutions– 11 Questions
Access Answers of Maths NCERT Class 10 Chapter 4 – Quadratic Equations Exercise 4.4
1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
Solutions:
(i) Given,
2x2 – 3x + 5 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -3 and c = 5
We know, discriminant = b2 – 4ac
= ( – 3)2 – 4 (2) (5) = 9 – 40
= – 31
As you can see, b2 – 4ac < 0
Therefore, no real root is possible for the given equation, 2x2 – 3x + 5 = 0.
(ii) 3x2 – 4√3x + 4 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = -4√3 and c = 4
We know, Discriminant = b2 – 4ac
= (-4√3)2 – 4(3)(4)
= 48 – 48 = 0
As b2 – 4ac = 0,
Real roots exist for the given equation, and they are equal to each other.
Hence, the roots will be –b/2a and –b/2a.
–b/2a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
(iii) 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -6, c = 3
As we know, discriminant = b2 – 4ac
= (-6)2 – 4 (2) (3)
= 36 – 24 = 12
As b2 – 4ac > 0,
Therefore, there are distinct real roots that exist for this equation, 2x2 – 6x + 3 = 0.
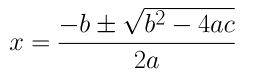
= (-(-6) ± √(-62-4(2)(3)) )/ 2(2)
= (6±2√3 )/4
= (3±√3)/2
Therefore, the roots for the given equation are (3+√3)/2 and (3-√3)/2.
2. Find the values of k for each of the following quadratic equations so that they have two equal roots.
(i) 2x2 + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solutions:
(i) 2x2 + kx + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 2, b = k and c = 3
As we know, discriminant = b2 – 4ac
= (k)2 – 4(2) (3)
= k2 – 24
For equal roots, we know,
Discriminant = 0
k2 – 24 = 0
k2 = 24
k = ±√24 = ±2√6
(ii) kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = k, b = – 2k and c = 6
We know, Discriminant = b2 – 4ac
= ( – 2k)2 – 4 (k) (6)
= 4k2 – 24k
For equal roots, we know,
b2 – 4ac = 0
4k2 – 24k = 0
4k (k – 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x2‘ and ‘x‘.
Therefore, if this equation has two equal roots, k should be 6 only.
3. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2? If so, find its length and breadth.
Solution:
Let the breadth of the mango grove be l.
The length of the mango grove will be 2l.
Area of the mango grove = (2l) (l)= 2l2
2l2 = 800
l2 = 800/2 = 400
l2 – 400 =0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = 0, c = 400
As we know, discriminant = b2 – 4ac
=> (0)2 – 4 × (1) × ( – 400) = 1600
Here, b2 – 4ac > 0
Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ±20
As we know, the value of length cannot be negative.
Therefore, the breadth of the mango grove = 20 m.
Length of the mango grove = 2 × 20 = 40 m.
4. Is the following situation possible? If so, determine their present ages. The sum of the ages of the two friends is 20 years. Four years ago, the product of their age in years was 48.
Solution:
Let’s say the age of one friend is x years.
Then, the age of the other friend will be (20 – x) years.
Four years ago,
Age of first friend = (x – 4) years
Age of second friend = (20 – x – 4) = (16 – x) years
As per the given question, we can write,
(x – 4) (16 – x) = 48
16x – x2 – 64 + 4x = 48
– x2 + 20x – 112 = 0
x2 – 20x + 112 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -20 and c = 112
Discriminant = b2 – 4ac
= (-20)2 – 4 × 112
= 400 – 448 = -48
b2 – 4ac < 0
Therefore, there will be no real solution possible for the equations. Hence, the condition doesn’t exist.
5. Is it possible to design a rectangular park with a perimeter of 80 and an area of 400 m2? If so, find its length and breadth.
Solution:
Let the length and breadth of the park be l and b.
Perimeter of the rectangular park = 2 (l + b) = 80
So, l + b = 40
Or, b = 40 – l
Area of the rectangular park = l×b = l(40 – l) = 40l – l2 = 400
l2 – 40l + 400 = 0, which is a quadratic equation.
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -40, c = 400
Since discriminant = b2 – 4ac
=(-40)2 – 4 × 400
= 1600 – 1600 = 0
Thus, b2 – 4ac = 0
Therefore, this equation has equal real roots. Hence, the situation is possible.
The root of the equation,
l = –b/2a
l = -(-40)/2(1) = 40/2 = 20
Therefore, the length of the rectangular park, l = 20 m
And the breadth of the park, b = 40 – l = 40 – 20 = 20 m.
Key Features of NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.4
- Subject experts have provided the solutions after a lot of brainstorming.
- The answers are accurate.
- Each question in the NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.4 is explained in a stepwise manner.
- The solutions will help students score well in the board examinations.





Nice I love byjus…..
Thanks