NCERT Solutions for Class 9 Maths Chapter 7 – CBSE Free PDF Download
NCERT Solutions for Class 9 Maths Chapter 7 Triangles provides the answers and questions related to the chapter as included in the CBSE Syllabus for 2023-24. The word triangle itself describes its meaning. “Tri” means “three”,; so a closed figure formed by three intersecting lines is known as a Triangle. Students must have already studied the angle sum property of a triangle in Chapter 6 of NCERT Class 9 Maths. Now, in continuation to it, Chapter 7 of NCERT Solutions for Class 9 Maths will brief students about the congruence of triangles and the rules of congruence. Also, they will learn a few more properties of triangles and inequalities in a triangle.
Download Exclusively Curated Chapter Notes for Class 9 Maths Chapter – 7 Goemetry of Triangles
Download Most Important Questions for Class 9 Maths Chapter – 7 Goemetry of Triangles
Here we have provided the complete Class 9 Maths NCERT Solutions Chapter 7 Triangles in PDF format solved by experienced teachers. Students can download the free PDF of these NCERT Solutions for Class 9 by clicking on the link below to keep it handy for future reference.
NCERT Solutions for Class 9 Maths Chapter 7 – Triangles
List of Exercises in NCERT Class 9 Maths Chapter 7
Exercise 7.1 Solution 8 Questions (6 Short Answer Questions, 2 Long Answer Question)
Exercise 7.2 Solution 8 Questions (6 Short Answer Questions, 2 Long Answer Question)
Exercise 7.3 Solution 5 Questions (3 Short Answer Questions, 2 Long Answer Question)
Exercise 7.4 Solution 6 Questions (5 Short Answer Questions, 1 Long Answer Question)
Exercise 7.5 (Optional) Solution 4 Questions
Access Answers of Maths NCERT Class 9 Chapter 7 – Triangles
Exercise: 7.1 (Page No: 118)
1. In quadrilateral ACBD, AC = AD and AB bisect ∠A (see Fig. 7.16). Show that ΔABC≅ ΔABD. What can you say about BC and BD?

Solution:
It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects ∠A.
We will have to now prove that the two triangles ABC and ABD are similar i.e. ΔABC ≅ ΔABD
Proof:
Consider the triangles ΔABC and ΔABD,
(i) AC = AD (It is given in the question)
(ii) AB = AB (Common)
(iii) ∠CAB = ∠DAB (Since AB is the bisector of angle A)
So, by SAS congruency criterion, ΔABC ≅ ΔABD.
For the 2nd part of the question, BC and BD are of equal lengths by the rule of C.P.C.T.

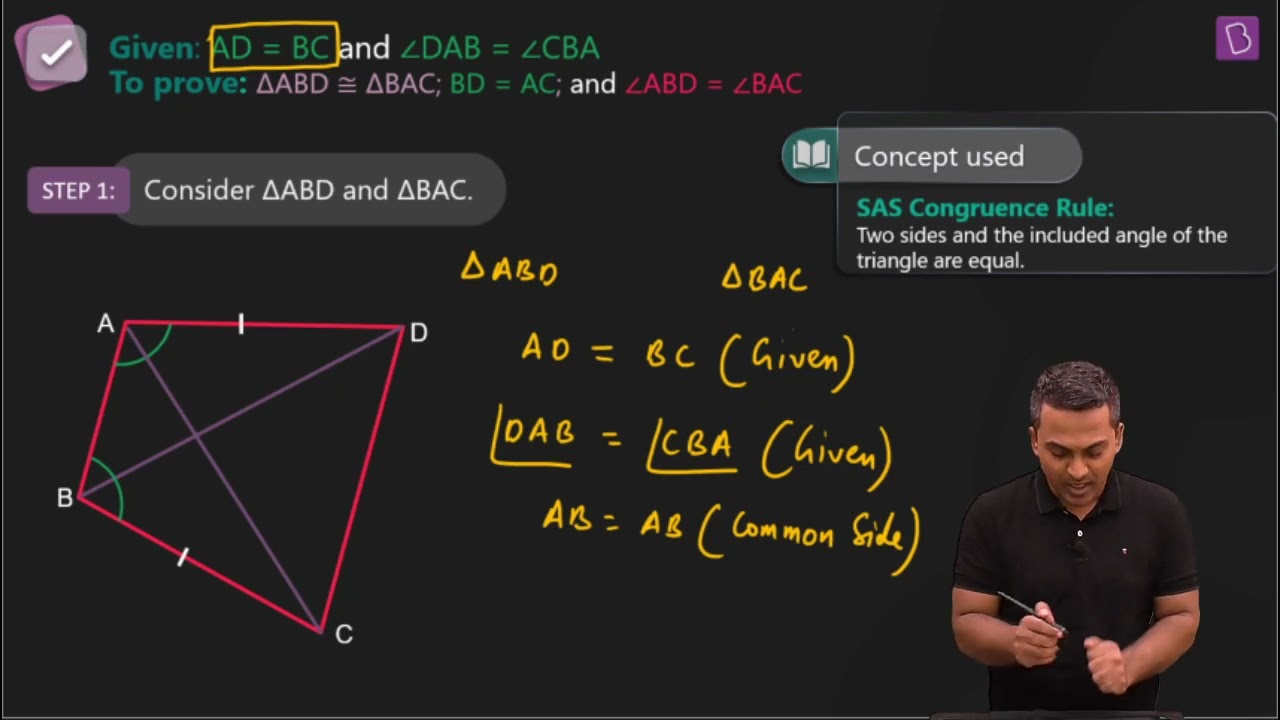
2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

Solution:
The given parameters from the questions are ∠DAB = ∠CBA and AD = BC.
(i) ΔABD and ΔBAC are similar by SAS congruency as
AB = BA (It is the common arm)
∠DAB = ∠CBA and AD = BC (These are given in the question)
So, triangles ABD and BAC are similar i.e. ΔABD ≅ ΔBAC. (Hence proved).
(ii) It is now known that ΔABD ≅ ΔBAC so,
BD = AC (by the rule of CPCT).
(iii) Since ΔABD ≅ ΔBAC so,
Angles ∠ABD = ∠BAC (by the rule of CPCT).
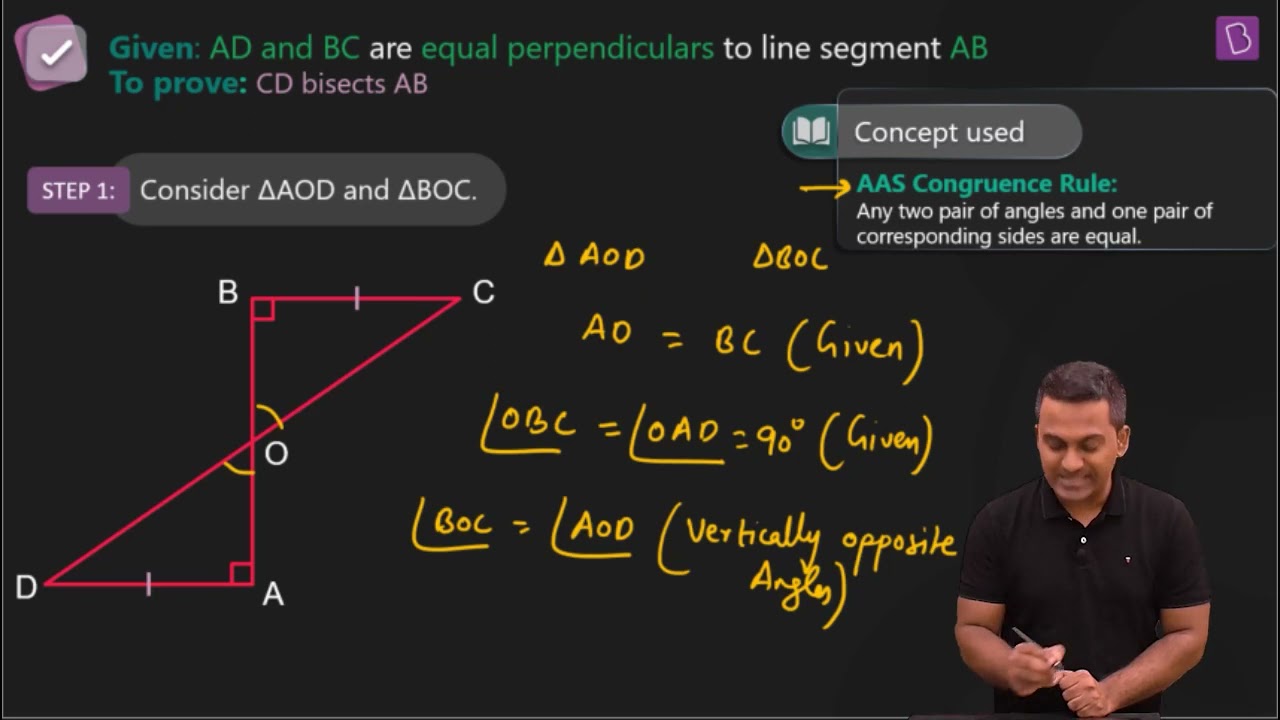
3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

Solution:
It is given that AD and BC are two equal perpendiculars to AB.
We will have to prove that CD is the bisector of AB
Now,
Triangles ΔAOD and ΔBOC are similar by AAS congruency since:
(i) ∠A = ∠B (They are perpendiculars)
(ii) AD = BC (As given in the question)
(iii) ∠AOD = ∠BOC (They are vertically opposite angles)
∴ ΔAOD ≅ ΔBOC.
So, AO = OB (by the rule of CPCT).
Thus, CD bisects AB (Hence proved).
4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC ≅ ΔCDA.

Solution:
It is given that p || q and l || m
To prove:
Triangles ABC and CDA are similar i.e. ΔABC ≅ ΔCDA
Proof:
Consider the ΔABC and ΔCDA,
(i) ∠BCA = ∠DAC and ∠BAC = ∠DCA Since they are alternate interior angles
(ii) AC = CA as it is the common arm
So, by ASA congruency criterion, ΔABC ≅ ΔCDA.
5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

Solution:
It is given that the line “l” is the bisector of angle ∠A and the line segments BP and BQ are perpendiculars drawn from l.
(i) ΔAPB and ΔAQB are similar by AAS congruency because:
∠P = ∠Q (They are the two right angles)
AB = AB (It is the common arm)
∠BAP = ∠BAQ (As line l is the bisector of angle A)
So, ΔAPB ≅ ΔAQB.
(ii) By the rule of CPCT, BP = BQ. So, it can be said the point B is equidistant from the arms of ∠A.

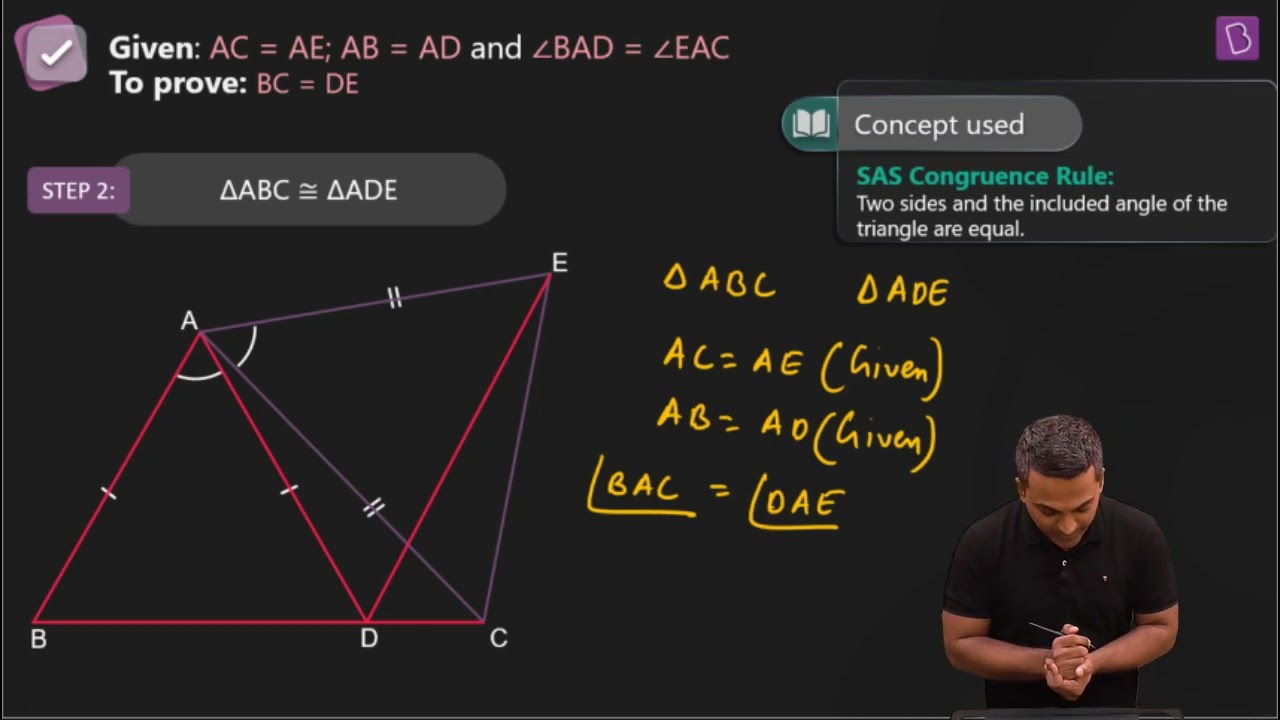
6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Solution:
It is given in the question that AB = AD, AC = AE, and ∠BAD = ∠EAC
To prove:
The line segment BC and DE are similar i.e. BC = DE
Proof:
We know that ∠BAD = ∠EAC
Now, by adding ∠DAC on both sides we get,
∠BAD + ∠DAC = ∠EAC +∠DAC
This implies, ∠BAC = ∠EAD
Now, ΔABC and ΔADE are similar by SAS congruency since:
(i) AC = AE (As given in the question)
(ii) ∠BAC = ∠EAD
(iii) AB = AD (It is also given in the question)
∴ Triangles ABC and ADE are similar i.e. ΔABC ≅ ΔADE.
So, by the rule of CPCT, it can be said that BC = DE.
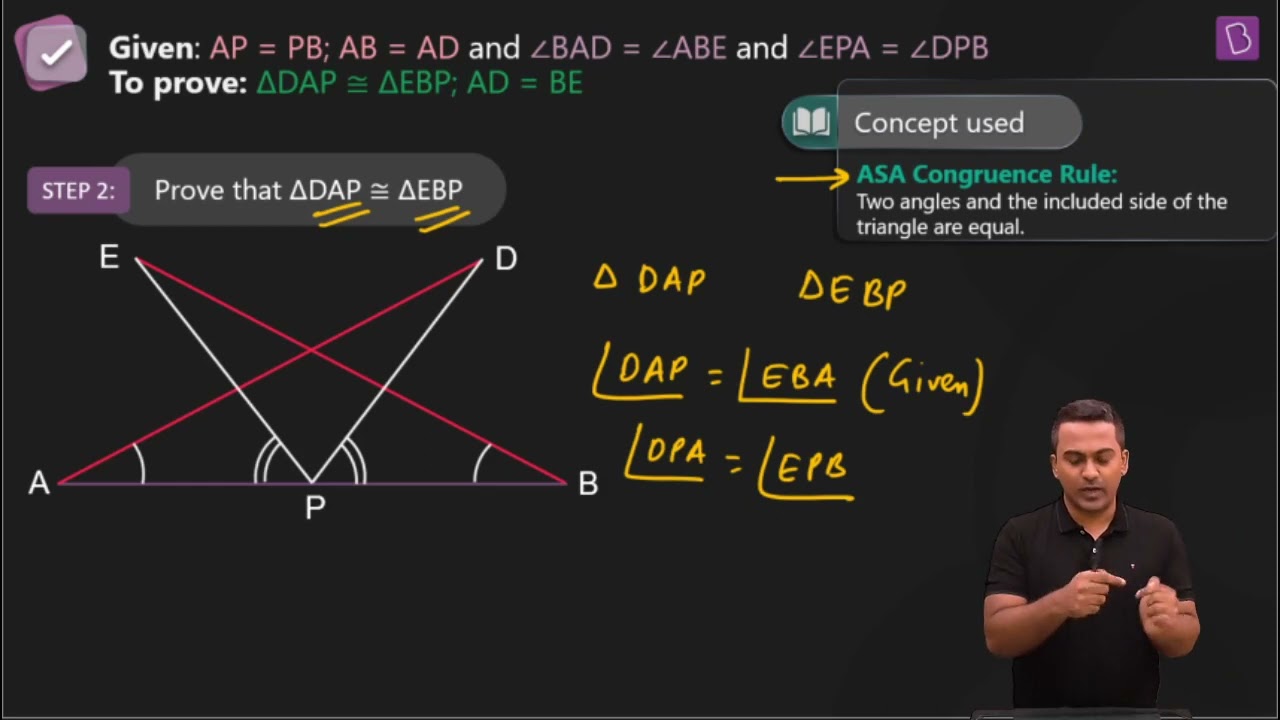
7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE

Solutions:
In the question, it is given that P is the mid-point of line segment AB. Also, ∠BAD = ∠ABE and ∠EPA = ∠DPB
(i) It is given that ∠EPA = ∠DPB
Now, add ∠DPE on both sides,
∠EPA +∠DPE = ∠DPB+∠DPE
This implies that angles DPA and EPB are equal i.e. ∠DPA = ∠EPB
Now, consider the triangles DAP and EBP.
∠DPA = ∠EPB
AP = BP (Since P is the mid-point of the line segment AB)
∠BAD = ∠ABE (As given in the question)
So, by ASA congruency, ΔDAP ≅ ΔEBP.
(ii) By the rule of CPCT, AD = BE.
8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle.
(iii) ΔDBC ≅ ΔACB
(iv) CM = ½ AB

Solution:
It is given that M is the mid-point of the line segment AB, ∠C = 90°, and DM = CM
(i) Consider the triangles ΔAMC and ΔBMD:
AM = BM (Since M is the mid-point)
CM = DM (Given in the question)
∠CMA = ∠DMB (They are vertically opposite angles)
So, by SAS congruency criterion, ΔAMC ≅ ΔBMD.
(ii) ∠ACM = ∠BDM (by CPCT)
∴ AC || BD as alternate interior angles are equal.
Now, ∠ACB +∠DBC = 180° (Since they are co-interiors angles)
⇒ 90° +∠B = 180°
∴ ∠DBC = 90°
(iii) In ΔDBC and ΔACB,
BC = CB (Common side)
∠ACB = ∠DBC (They are right angles)
DB = AC (by CPCT)
So, ΔDBC ≅ ΔACB by SAS congruency.
(iv) DC = AB (Since ΔDBC ≅ ΔACB)
⇒ DM = CM = AM = BM (Since M the is mid-point)
So, DM + CM = BM+AM
Hence, CM + CM = AB
⇒ CM = (½) AB
Exercise: 7.2 (Page No: 123)
1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC (ii) AO bisects ∠A

Solution:
Given:
AB = AC and
the bisectors of ∠B and ∠C intersect each other at O
(i) Since ABC is an isosceles with AB = AC,
∠B = ∠C
½ ∠B = ½ ∠C
⇒ ∠OBC = ∠OCB (Angle bisectors)
∴ OB = OC (Side opposite to the equal angles are equal.)
(ii) In ΔAOB and ΔAOC,
AB = AC (Given in the question)
AO = AO (Common arm)
OB = OC (As Proved Already)
So, ΔAOB ≅ ΔAOC by SSS congruence condition.
BAO = CAO (by CPCT)
Thus, AO bisects ∠A.
2. In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.

Solution:
It is given that AD is the perpendicular bisector of BC
To prove:
AB = AC
Proof:
In ΔADB and ΔADC,
AD = AD (It is the Common arm)
∠ADB = ∠ADC
BD = CD (Since AD is the perpendicular bisector)
So, ΔADB ≅ ΔADC by SAS congruency criterion.
Thus,
AB = AC (by CPCT)
3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

Solution:
Given:
(i) BE and CF are altitudes.
(ii) AC = AB
To prove:
BE = CF
Proof:
Triangles ΔAEB and ΔAFC are similar by AAS congruency since
∠A = ∠A (It is the common arm)
∠AEB = ∠AFC (They are right angles)
AB = AC (Given in the question)
∴ ΔAEB ≅ ΔAFC and so, BE = CF (by CPCT).
4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Solution:
It is given that BE = CF
(i) In ΔABE and ΔACF,
∠A = ∠A (It is the common angle)
∠AEB = ∠AFC (They are right angles)
BE = CF (Given in the question)
∴ ΔABE ≅ ΔACF by AAS congruency condition.
(ii) AB = AC by CPCT and so, ABC is an isosceles triangle.
5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.

Solution:
In the question, it is given that ABC and DBC are two isosceles triangles.
We will have to show that ∠ABD = ∠ACD
Proof:
Triangles ΔABD and ΔACD are similar by SSS congruency since
AD = AD (It is the common arm)
AB = AC (Since ABC is an isosceles triangle)
BD = CD (Since BCD is an isosceles triangle)
So, ΔABD ≅ ΔACD.
∴ ∠ABD = ∠ACD by CPCT.
6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.

Solution:
It is given that AB = AC and AD = AB
We will have to now prove ∠BCD is a right angle.
Proof:
Consider ΔABC,
AB = AC (It is given in the question)
Also, ∠ACB = ∠ABC (They are angles opposite to the equal sides and so, they are equal)
Now, consider ΔACD,
AD = AB
Also, ∠ADC = ∠ACD (They are angles opposite to the equal sides and so, they are equal)
Now,
In ΔABC,
∠CAB + ∠ACB + ∠ABC = 180°
So, ∠CAB + 2∠ACB = 180°
⇒ ∠CAB = 180° – 2∠ACB — (i)
Similarly, in ΔADC,
∠CAD = 180° – 2∠ACD — (ii)
also,
∠CAB + ∠CAD = 180° (BD is a straight line.)
Adding (i) and (ii) we get,
∠CAB + ∠CAD = 180° – 2∠ACB+180° – 2∠ACD
⇒ 180° = 360° – 2∠ACB-2∠ACD
⇒ 2(∠ACB+∠ACD) = 180°
⇒ ∠BCD = 90°
7. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution:

In the question, it is given that
∠A = 90° and AB = AC
AB = AC
⇒ ∠B = ∠C (They are angles opposite to the equal sides and so, they are equal)
Now,
∠A+∠B+∠C = 180° (Since the sum of the interior angles of the triangle)
∴ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
So, ∠B = ∠C = 45°
8. Show that the angles of an equilateral triangle are 60° each.
Solution:
Let ABC be an equilateral triangle as shown below:

Here, BC = AC = AB (Since the length of all sides is same)
⇒ ∠A = ∠B =∠C (Sides opposite to the equal angles are equal.)
Also, we know that
∠A+∠B+∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
So, the angles of an equilateral triangle are always 60° each.
Exercise: 7.3 (Page No: 128)
1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

Solution:
In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.
(i) ΔABD and ΔACD are similar by SSS congruency because:
AD = AD (It is the common arm)
AB = AC (Since ΔABC is isosceles)
BD = CD (Since ΔDBC is isosceles)
∴ ΔABD ≅ ΔACD.
(ii) ΔABP and ΔACP are similar as:
AP = AP (It is the common side)
∠PAB = ∠PAC (by CPCT since ΔABD ≅ ΔACD)
AB = AC (Since ΔABC is isosceles)
So, ΔABP ≅ ΔACP by SAS congruency condition.
(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.
AP bisects ∠A. — (i)
Also, ΔBPD and ΔCPD are similar by SSS congruency as
PD = PD (It is the common side)
BD = CD (Since ΔDBC is isosceles.)
BP = CP (by CPCT as ΔABP ≅ ΔACP)
So, ΔBPD ≅ ΔCPD.
Thus, ∠BDP = ∠CDP by CPCT. — (ii)
Now by comparing (i) and (ii) it can be said that AP bisects ∠A as well as ∠D.
(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ΔCPD)
and BP = CP — (i)
also,
∠BPD +∠CPD = 180° (Since BC is a straight line.)
⇒ 2∠BPD = 180°
⇒ ∠BPD = 90° —(ii)
Now, from equations (i) and (ii), it can be said that
AP is the perpendicular bisector of BC.
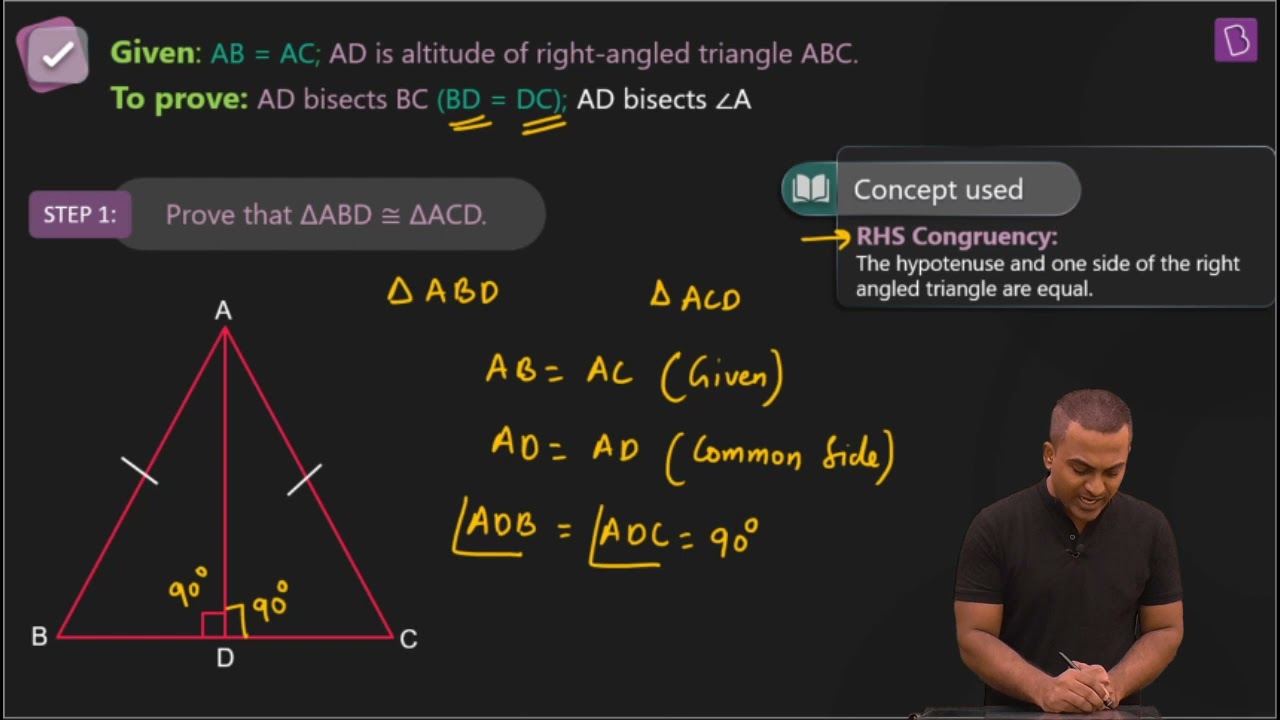
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
Solution:
It is given that AD is an altitude and AB = AC. The diagram is as follows:

(i) In ΔABD and ΔACD,
∠ADB = ∠ADC = 90°
AB = AC (It is given in the question)
AD = AD (Common arm)
∴ ΔABD ≅ ΔACD by RHS congruence condition.
Now, by the rule of CPCT,
BD = CD.
So, AD bisects BC
(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD
Hence, AD bisects ∠A.
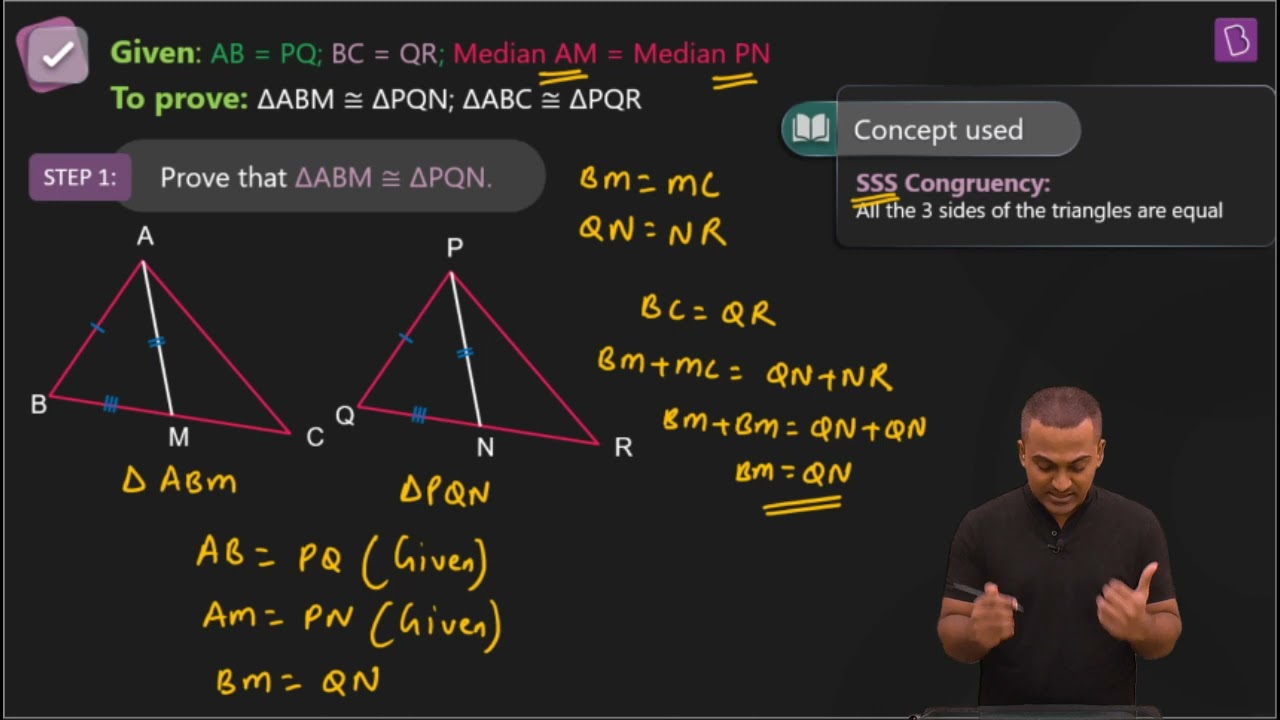
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR

Solution:
Given parameters are:
AB = PQ,
BC = QR and
AM = PN
(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)
Also, BC = QR
So, ½ BC = ½ QR
⇒ BM = QN
In ΔABM and ΔPQN,
AM = PN and AB = PQ (As given in the question)
BM = QN (Already proved)
∴ ΔABM ≅ ΔPQN by SSS congruency.
(ii) In ΔABC and ΔPQR,
AB = PQ and BC = QR (As given in the question)
∠ABC = ∠PQR (by CPCT)
So, ΔABC ≅ ΔPQR by SAS congruency.
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
 .
.
Solution:
It is known that BE and CF are two equal altitudes.
Now, in ΔBEC and ΔCFB,
∠BEC = ∠CFB = 90° (Same Altitudes)
BC = CB (Common side)
BE = CF (Common side)
So, ΔBEC ≅ ΔCFB by RHS congruence criterion.
Also, ∠C = ∠B (by CPCT)
Therefore, AB = AC as sides opposite to the equal angles is always equal.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:

In the question, it is given that AB = AC
Now, ΔABP and ΔACP are similar by RHS congruency as
∠APB = ∠APC = 90° (AP is altitude)
AB = AC (Given in the question)
AP = AP (Common side)
So, ΔABP ≅ ΔACP.
∴ ∠B = ∠C (by CPCT)
Exercise: 7.4 (Page No: 132)
1. Show that in a right-angled triangle, the hypotenuse is the longest side.

Solution:
It is known that ABC is a triangle right angled at B.
We know that,
∠A +∠B+∠C = 180°
Now, if ∠B+∠C = 90° then ∠A has to be 90°.
Since A is the largest angle of the triangle, the side opposite to it must be the largest.
So, AB is the hypotenuse which will be the largest side of the above right-angled triangle i.e. ΔABC.

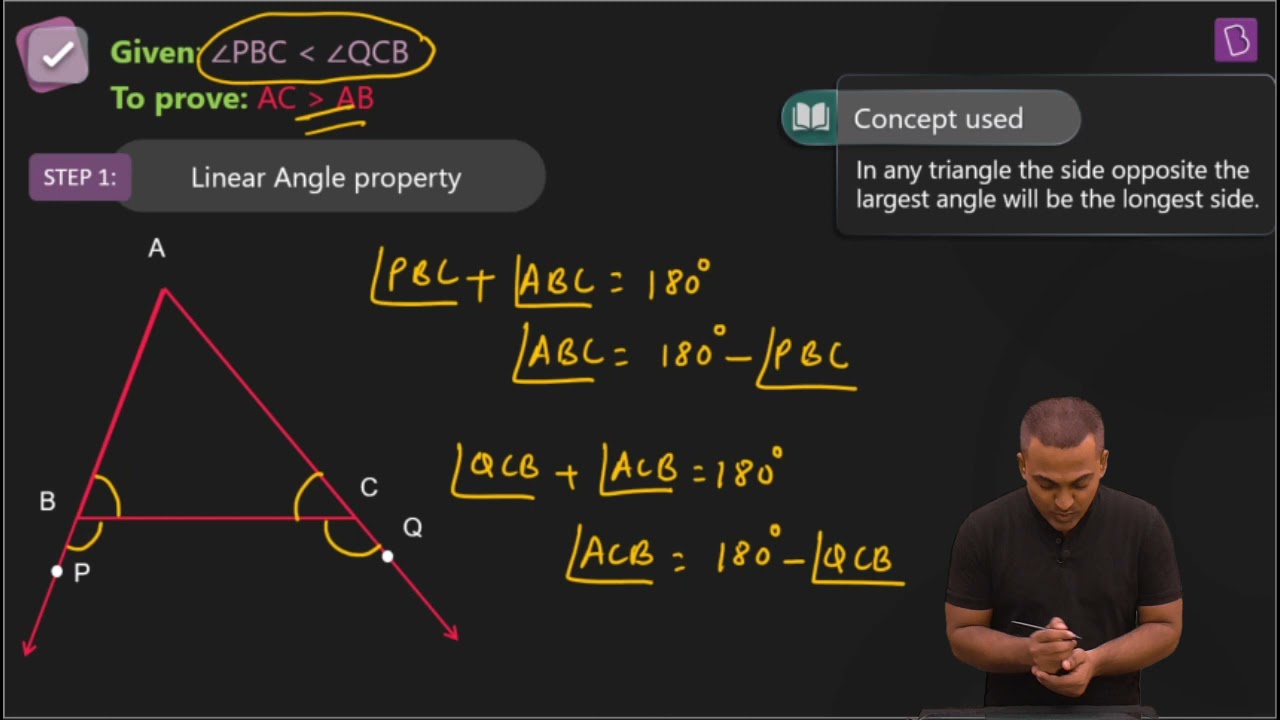
2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

Solution:
It is given that ∠PBC < ∠QCB
We know that ∠ABC + ∠PBC = 180°
So, ∠ABC = 180°-∠PBC
Also,
∠ACB +∠QCB = 180°
Therefore ∠ACB = 180° -∠QCB
Now, since ∠PBC < ∠QCB,
∴ ∠ABC > ∠ACB
Hence, AC > AB as sides opposite to the larger angle is always larger.
3. In Fig. 7.49, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Solution:
In the question, it is mentioned that angles B and angle C is smaller than angles A and D respectively i.e. ∠B < ∠A and ∠C < ∠D.
Now,
Since the side opposite to the smaller angle is always smaller
AO < BO — (i)
And OD < OC —(ii)
By adding equation (i) and equation (ii) we get
AO+OD < BO + OC
So, AD < BC
4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50).
Show that ∠A > ∠C and ∠B > ∠D.

Solution:
In ΔABD, we see that
AB < AD < BD
So, ∠ADB < ∠ABD — (i) (Since angle opposite to longer side is always larger)
Now, in ΔBCD,
BC < DC < BD
Hence, it can be concluded that
∠BDC < ∠CBD — (ii)
Now, by adding equation (i) and equation (ii) we get,
∠ADB + ∠BDC < ∠ABD + ∠CBD
∠ADC < ∠ABC
∠B > ∠D
Similarly, In triangle ABC,
∠ACB < ∠BAC — (iii) (Since the angle opposite to the longer side is always larger)
Now, In ΔADC,
∠DCA < ∠DAC — (iv)
By adding equation (iii) and equation (iv) we get,
∠ACB + ∠DCA < ∠BAC+∠DAC
⇒ ∠BCD < ∠BAD
∴ ∠A > ∠C

5. In Fig 7.51, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR > ∠PSQ.

Solution:
It is given that PR > PQ and PS bisects ∠QPR
Now we will have to prove that angle PSR is smaller than PSQ i.e. ∠PSR > ∠PSQ
Proof:
∠QPS = ∠RPS — (ii) (As PS bisects ∠QPR)
∠PQR > ∠PRQ — (i) (Since PR > PQ as angle opposite to the larger side is always larger)
∠PSR = ∠PQR + ∠QPS — (iii) (Since the exterior angle of a triangle equals to the sum of opposite interior angles)
∠PSQ = ∠PRQ + ∠RPS — (iv) (As the exterior angle of a triangle equals to the sum of opposite interior angles)
By adding (i) and (ii)
∠PQR +∠QPS > ∠PRQ +∠RPS
Thus, from (i), (ii), (iii) and (iv), we get
∠PSR > ∠PSQ
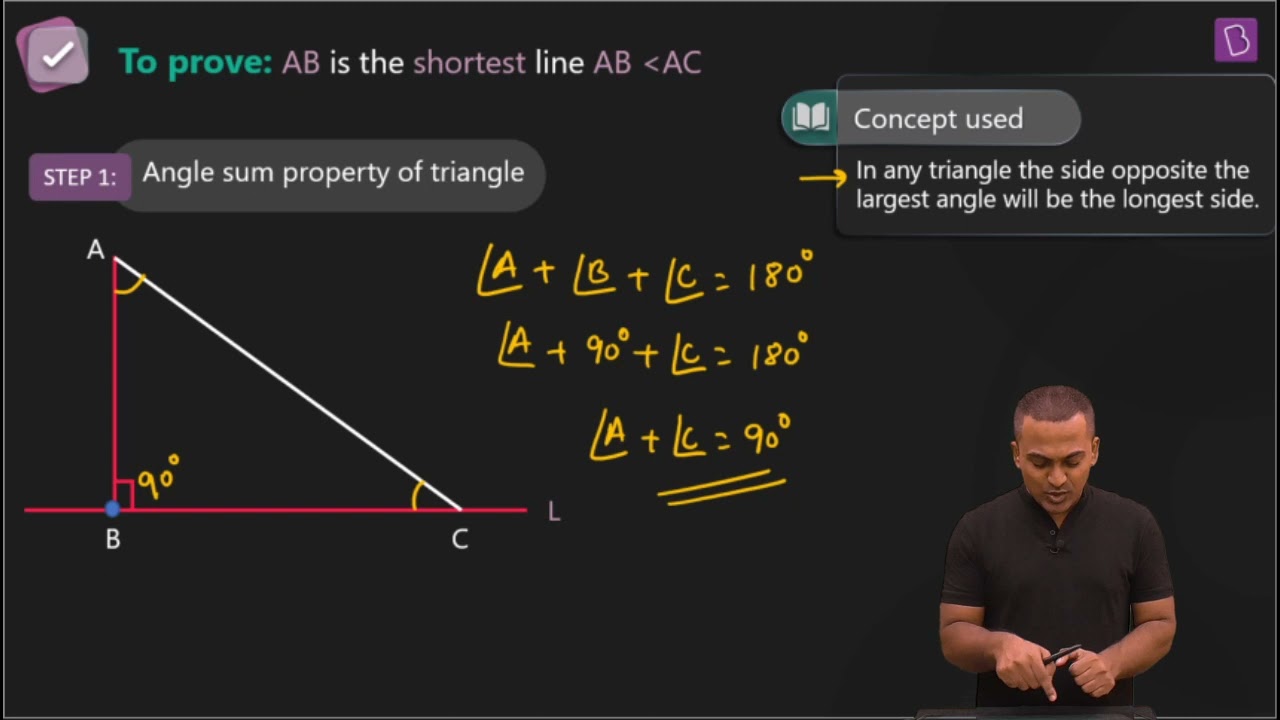
6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Solution:
First, let “l” be a line segment and “B” be a point lying on it. A line AB perpendicular to l is now drawn. Also, let C be any other point on l. The diagram will be as follows:

To prove:
AB < AC
Proof:
In ΔABC, ∠B = 90°
Now, we know that
∠A+∠B+∠C = 180°
∴ ∠A +∠C = 90°
Hence, ∠C must be an acute angle which implies ∠C < ∠B
So, AB < AC (As the side opposite to the larger angle is always larger)
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 7 |
| CBSE Notes for Class 9 Maths Chapter 7 |
Summary of NCERT Solutions for Class 9 Maths Chapter 7 Triangles
Triangle is a part of Geometry. However, the complete Geometry of Class 9 constitutes a weightage of 22 marks out of 80 marks. Have a look at the types of questions that are expected from Geometry in the annual exam of class 9 Maths paper.
| NCERT Class 9 Maths Geometry – Marks Distribution | |||
| Topics | Multiple Choice Questions | Short Questions | Long Questions |
| Introduction to Euclid’s Geometry, Lines and Angles, Triangles, Quadrilaterals, Areas, Circles, Constructions | 4 Qs of 1 mark each | 2 Qs of 3 marks each | 2 Qs of 6 marks each |
| Total Marks | 4 Marks | 6 Marks | 12 Marks |
Students should practise all the questions from the exercise to score high marks in the Class 9 Maths paper. The step-by-step solution to all the exercises of NCERT Class 9 Maths Chapter 7 is provided below:
In previous classes, students must have used the properties of triangles for solving the questions, but now in the NCERT Textbook of Class 9 Maths Chapter 7, students will learn how to prove these properties. For solving the questions related to this topic, it is very necessary that students should know the congruence rule. First, go through the theory and then look at the solved examples that are already there in the book. After that, start solving the exercise problems.
Students can also have a look at the NCERT Solutions of Class 9 for Science subject to know the answers of all the chapters with a detailed explanation.
Important Concepts Learned in NCERT Class 9 Maths Chapter 7 – Triangles
The aim of including this Triangle Chapter in the Class 9 Maths NCERT textbook is to make students know the following concepts:
- Congruence of triangles.
- Criteria for congruence of triangles (SAS congruence rule, ASA congruence rule, SSS congruence rule, RHS congruence rule).
- Properties of triangles.
- Inequalities of triangles.
We hope this information on “NCERT Solution Class 9 Maths Chapter 7” is useful for students. Click on NCERT Solutions to get the solved answers from the NCERT book for all the classes. Stay tuned for further updates on CBSE and other competitive exams. To access interactive Maths and Science Videos, download BYJU’S App and subscribe to our YouTube Channel.
Triangles is a very important chapter as the fundamental concepts introduced here are carried forward to higher levels of education. For this purpose, after completing the questions from the NCERT Textbook, students are recommended to solve the other textbooks which are prescribed by the CBSE Board.
Disclaimer:
Dropped Topics – 7.6 Inequalities in triangles.
Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 7
List out the important topics covered in NCERT Solutions for Class 9 Maths Chapter 7.
1. Congruence of triangles.
2. Criteria for congruence of triangles (SAS congruence rule, ASA congruence rule, SSS congruence rule, RHS congruence rule).
3. Properties of triangles.
4. Inequalities of triangles.





















Comments