Triangles Class 9 Notes - Chapter 7

CBSE Class 9 Maths Triangles Notes:-Download PDF Here

Introduction:

The concepts covered in Triangles Class 9 are important since they are carried on to higher education levels. For this reason, students are advised to learn the concept completely. The purpose of incorporating “Triangles” chapter in the NCERT textbook for Class 9 Maths is to teach students the following concepts:

• Triangle congruence
• SAS, ASA, SSS and RHS Congruence Rule
• Triangle Properties
• Triangle Inequalities

Congruent Triangles

In a pair of triangles if all three corresponding sides and three corresponding angles are exactly equal, then the triangles are said to be congruent.

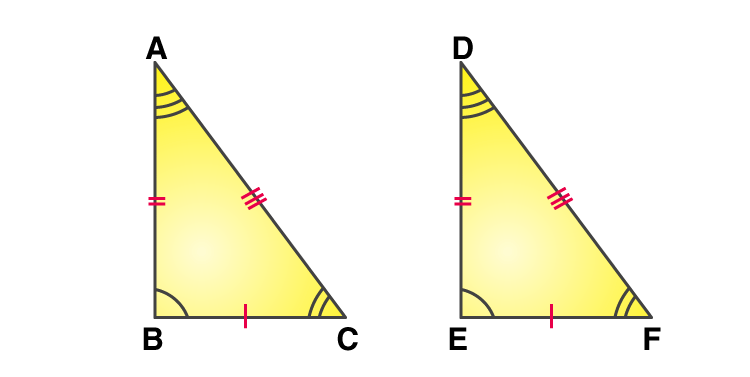
In congruent triangles, the corresponding parts are equal and are written as CPCT (Corresponding part of the congruent triangle).

Video Lesson on Congruent Triangles

To know more about Congruency of Triangles, visit here.

Criteria for Congruency

Learning the congruence of triangles is very important to draw conclusions from the different polygon congruences. It has been used in real life, such as the construction of identical buildings, and so on. The following are the criteria for the congruency of the triangles.

• • SAS
  • ASA
  • AAS

• SSS
• RHS

symbolically, it is expressed as $\Delta ABC\cong \Delta XYZ$

SSS Criteria for Congruency

• If the three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
• If all sides are exactly the same, then their corresponding angles must also be exactly the same.

SAS Criteria for Congruency

– Axiom: Two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle.

ASA Criteria for Congruency

– Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle

Video Lesson on SAS And ASA Congruence Rule

AAS Criteria for Congruency

– Two triangles are said to be congruent to each other if two angles and one side of one triangle are equal to two angles and one side of the other triangle.

Why Are SSA and AAA Congruency rules Not Valid?

• SSA test is not a valid test for congruency as the angle is not included between the pairs of equal sides.
• The AAA test also is not a valid test as even though 2 triangles can have all three same angles, the sides can be of differing lengths. This becomes a test for similarity (AA).

Angles of a triangle

RHS Criteria for Congruency

• If in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
• RHS stands for Right angle – Hypotenuse – Side.

Properties of Isosceles Triangle

Isosceles Triangle Property

Angles opposite to equal sides of an isosceles triangle are equal.

Converse of Isosceles Triangle Property

The sides opposite the equal angles of a triangle are equal.

To know more about the Properties of Isosceles Triangles, visit here.

Inequalities in Triangles

Relationship between unequal sides of the triangle and the angles opposite to it.

If 2 sides of a triangle are unequal, then the angle opposite to the longer side will be larger than the angle opposite to the shorter side.

Triangle Inequality

The sum of the lengths of any two sides of a triangle must be greater than the third side.

Video Lesson on Triangles

To know more about Triangles Inequalities Theorem, visit here.

Register with BYJU’S – The Learning App and download the app to get all class-wise notes.