Congruence of Triangles

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.

The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. There are basically four congruence rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The corresponding sides and angles of congruent triangles are equal. Also, learn about Congruent Figures here.

Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angle with the same measure are congruent.

CPCT is the term, we come across when we learn about the congruent triangle. Let’s see the condition for triangles to be congruent with proof.

Congruent meaning in Maths

The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.

Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is the same as the other.

Congruent Triangles

A closed polygon made of three line segments forming three angles is known as a Triangle.

Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.

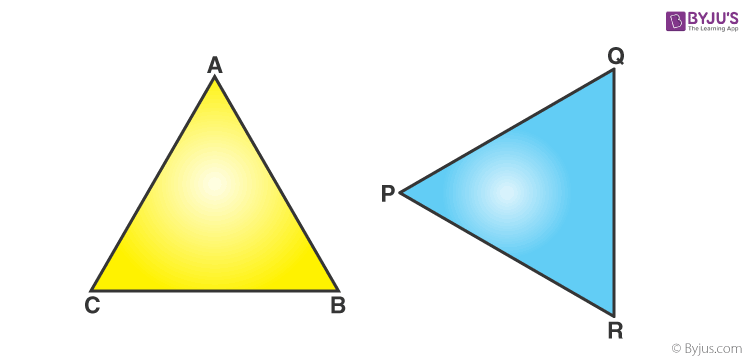
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,

Vertices:  A and P, B and Q, and C and R are the same.

Sides:  AB=PQ, QR= BC and AC=PR;

Angles:  ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.

Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence is denoted by the symbol “≅”.  From the above example, we can write ABC ≅ PQR. They have the same area and the same perimeter.

For More Information On Introduction To Congruent Triangles, Watch The Below Video:

CPCT Full Form

CPCT is the term we come across when we learn about the congruent triangle. CPCT means “Corresponding Parts of Congruent Triangles”. As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.

CPCT Rules in Maths

The full form of CPCT is Corresponding parts of Congruent triangles. After proving triangles congruent, the remaining dimension can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right angle-Hypotenuse-Side)

Let us learn them all in detail.

SSS (Side-Side-Side)

If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.

In the above-given figure, AB= PQ, BC = QR and AC=PR, hence Δ ABC ≅ Δ PQR.

SAS (Side-Angle-Side)

If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.

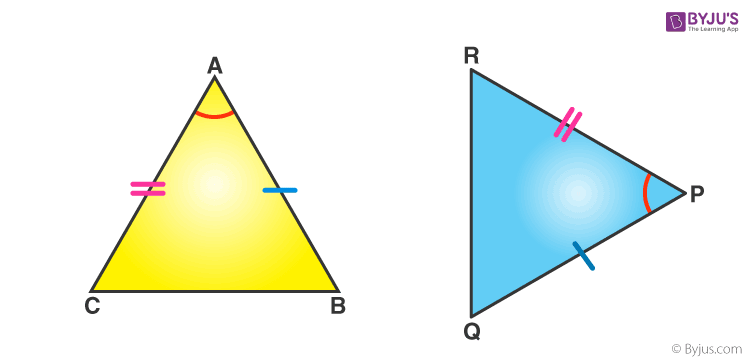
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.

ASA (Angle-Side- Angle)

If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.

In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.

For More Information On SAS And ASA Congruency Rules, Watch The Below Video:

AAS (Angle-Angle-Side) [Application of ASA]

AAS stands for Angle-Angle-Side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.

AAS congruence can be proved in easy steps.

Suppose we have two triangles ABC and DEF, where,

∠B = ∠E [Corresponding angles] ∠C = ∠F [Corresponding angles] And
AC = DF [Adjacent sides]

By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)

From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF

RHS (Right angle- Hypotenuse-Side)

If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.

In above figure, hypotenuse XZ = RT and side YZ=ST, hence  ∆ XYZ ≅ ∆ RST.

Solved Example

Let’s Work Out: Example 1: In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles. 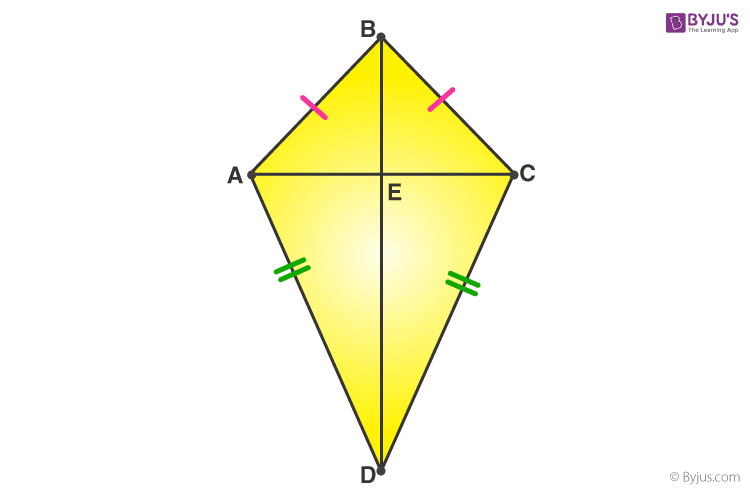Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC                                                (Given)AD = CD          (Given)BD = BD                                                (Common)Therefore, ∆ABD ≅ ∆CBD                      (By SSS congruency)∠ABD = ∠CBD                                      (CPCTC) Now, consider ∆ABE and ∆CBE, AB = BC                                                (Given) ∠ABD = ∠CBD                                      (Proved above) BE = BE                                                (Common) Therefore, ∆ABE≅ ∆CBE                       (By SAS congruency) ∠BEA = ∠BEC                                      (CPCTC) And ∠BEA +∠BEC = 180°                      (Linear pair) 2∠BEA = 180°                                       (∠BEA = ∠BEC) ∠BEA = 180°/2 = 90° = ∠BEC AE = EC                                                (CPCTC) Hence, BD is a perpendicular bisector of AC. Example 2: In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A. Solution: Given: In a Δ ABC, AB = AC and ∠B = 70° ∠ B = ∠ C [Angles opposite to equal sides of a triangle are equal] Therefore, ∠ B = ∠ C = 70° Sum of angles in a triangle = 180° ∠ A + ∠ B + ∠ C = 180° ∠ A + 70° + 70° = 180° ∠ A = 180° – 140° ∠ A = 40°

Practice Problems

Q.1: PQR is a triangle in which PQ = PR and is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Q.2: If perpendiculars from any point within an angle on its arms are congruent. Prove that it lies on the bisector of that angle.

Video Lesson

For more details visit and register with us at BYJU’S. Also, download BYJU’S-The Learning App to enjoy personalised learning.