In geometry, the triangle is one of the most important two-dimensional shapes with 3 sides. This is a type of polygon with the least number of sides. Triangles are classified into various types based on the measure of angles and sides such as acute angle triangle, right triangle, scalene triangle, etc. However, we can define some specific relations between triangles in consideration of their sides. Like similar figures, we do have similar triangles as well. In this article, you will learn the property of similarity of triangles, when we call two triangles are similar along with criterion of similarity of triangles in detail.
What is Similarity of triangles?
The similarity of triangles can be defined based on their properties. Two triangles are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).
These two are the main conditions for the similarity of triangles.
Criterion for Similarity of Triangles
The criterion of similarity of triangles include:
- AAA similarity criterion
- AA similarity criterion
- SSS similarity criterion
- SAS similarity criterion
All these criteria are used to solve many triangles problems in maths. Let us understand the meaning of the similarity criterion of triangles here.
| Criterion | Description |
| AAA | If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio, and hence the two triangles are similar (AAA similarity criterion). |
| AA | If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar (AA similarity criterion). |
| SSS | If in two triangles, corresponding sides are in the same ratio, then their corresponding angles are equal, and hence the triangles are similar (SSS similarity criterion). |
| SAS | If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are similar (SAS similarity criterion). |
Learn more about the criteria for similarity of triangles here.
Theorem and Proof
Theorem: If a line divides any two sides of a triangle in the same ratio, then the line is said to be parallel to the third side.

Let ABC be a triangle with sides AB, AC and BC. DE divides any two sides of the triangle in the same ratio.
Given: Line divides a triangle in the same ratio. Thus,
Proof:
Let us assume that DE is not parallel to BC. Now we draw DE’ which is assumed to be parallel to BC. So,
Therefore, from (1) and (2)
Now we add 1 to both sides,
According to the figure
This directly implies that
Hence DE is parallel to BC. This proves the similarity of triangles.
Solved Example
Let us take an example to observe the property of similarity of triangles:
Illustration 1:PQRS is a trapezium with PQ parallel to RS. The point X and Y are on the non-parallel sides PS and QR respectively such that XY is parallel to PQ. Show that
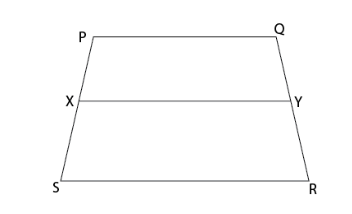
Solution: Let us first join PR in order to intersect XY at Z.
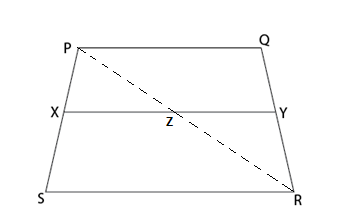
So,
In
So,
Similarly, from
From equation (3) and (4),

Learn various concepts like similar figures, trapezoids, etc. by visiting our site byjus.com and downloading BYJU’S – The Learning App.

Comments