Cube root of a number can be found by a very simple method which is the prime factorization method. Cube root is denoted by ‘∛ ‘ symbol. Example: ∛8 = ∛(2 × 2 × 2) = 2. Since, 8 is a perfect cube number, it is easy to find the cube root of a number.
Finding the cubic root of non-perfect cube number is a little complex process but can be mastered easily. To find the cube root of any number, we need to find a number which when multiplied three times by itself gives the original number.
Let us learn here finding cube root using prime factorisation method and solved examples. Also, find the cubes and cube roots of 1 to 15 numbers here in the table given.
Table of contents:
- Definition
- Finding Cube Root
- Cube Root Lists
- Cube root by Prime Factorisation
- Example Questions
- Video Lesson
- FAQs
Definition
The cube root of any number say ‘a’, is the number ‘b’, which satisfies the equation given below:
b3 = a
This can be represented as:
How to Find Cube Root of a Number
Cube root is the inverse process of calculating the cube of a number. It is denoted by the symbol ‘∛’. Let us see some examples here now.
To find the cube root of a number 27, we want a number which when multiplied thrice with itself shall give 27. We can write,
27 = 3 × 3× 3 = 33
Taking cubic root on both the sides;
or ∛27 = ∛33
Therefore, the cube-root of 27 is 3.
Please note that we will only consider the positive values cube roots of the natural numbers.
Cube Root of 2
Let us consider another example of number 2. Since 2 is not a perfect cube number. It is not easy to find the cube root of 2. With the help of the long division method, it is possible to find the cube roots for non-perfect cube numbers. The approximate value of the ∛2 is 1.260.
We can estimate the ∛2 by using the trick here.
Since, 2 = 1 x 1 x 2
Cube root of 2 is approximately equal to (1 + 1+2)/3 = 4/3 = 1.333..
Cube root of 4
Again 4 is a number, which is not a perfect cube. If we factorise it, we get:
4 = 2 x 2 x 1
Hence, we can see, we cannot find the cube root by simple factorisation here.
Again, if we use the shortcut method, we get:
∛4 is equal to (2+2+1)/3 = 1.67
The actual value of ∛4 is 1.587, which is approximately equal to 1.67.
Cubes and Cube Roots List of 1 to 15
| Number | Cube(a3) | Cube root ∛a |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 8 | 1.260 |
| 3 | 27 | 1.442 |
| 4 | 64 | 1.587 |
| 5 | 125 | 1.710 |
| 6 | 216 | 1.817 |
| 7 | 343 | 1.913 |
| 8 | 512 | 2.000 |
| 9 | 729 | 2.080 |
| 10 | 1000 | 2.154 |
| 11 | 1331 | 2.224 |
| 12 | 1728 | 2.289 |
| 13 | 2197 | 2.351 |
| 14 | 2744 | 2.410 |
| 15 | 3375 | 2.466 |
Also, read:
Cube Root By Prime Factorisation Method
We can find the cube-root of a number by the method of prime factorisation. Consider the following example for a clear understanding:
2744= 2 × 2× 2 × 7 ×7 × 7= (2 × 7 )3
Therefore, the cube root of 2744 = ∛2744 = 2 × 7 = 14
Finding Cube Root Using Division Method
For finding the cube root using the division method is similar to using the long division method or manual square method. Make a pair of 3 digit numbers from the back to front. Next step is to find the number whose cube root is less than or equal to the given number. Now, subtract the obtained number from the given number and write down in the second number. After this step, it is necessary to find the multiplication factor for the further process in the long division method, which comes by multiplying the first number obtained. Similarly continue the above process, to find the cube root of a number. This long division process is used when the given number is not a perfect cube number. Finding the cube root of a number using this process takes a long time.
Cube Root of 64
Since 64 is a perfect cube of 4, therefore, it is easy to find its cube-root by the prime factorisation method.
64 = 2 x 2 x 2 x 2 x 2 x 2
∛64 = ∛(2 x 2 x 2 x 2 x 2 x 2)
= 2 x 2
= 4
Cube Root of 216
Since, 216 is perfect cube of 6, hence we can find the cube root of 216 by factorisation.
216 = 2 x 2 x 2 x 3 x 3 x 3
∛216 = ∛(2 x 2 x 2 x 3 x 3 x 3)
∛216 = 2 x 3
∛216 = 6
Cube Root of 343
Let us find the cube root of 343 with the help of the the prime factorisation method.
Dividing 343 by smallest prime factor, till we get the remainder as 1. Follow the below steps;
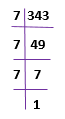
Cube root of 343
Therefore, 343 = 7 × 7 × 7
Cube Root of 512
To find the cube root of 512 we have to factorise it first.
The prime factorisation of 512 can be written as:
512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Taking the cube roots both the sides, we get;
∛512 = ∛(2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2)
∛512 = 2 x 2 x 2
∛512 = 8
Cube Root of 729
Now, let’s find the cubic root of 729.
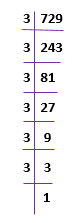
Cube root of 729
729 = 3 × 3 × 3 × 3 × 3 × 3 = 9 × 9 × 9
Therefore, the cube root of 729 i.e. ∛729 = 9
Cube Root Questions
Question 1: Solve: ∛24389
Solution:
Prime factors = 29×29×29 = 293
Therefore, ∛24389= 29.
Question 2: Find ∛46656 by the method of prime factorization.
Solution:
Let us first find the prime factors:
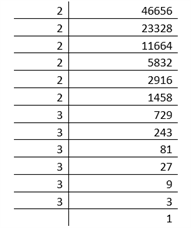
Cube Root of Numbers
∛46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 = 23 × 23 × 33 × 33 = (2 × 2 × 3 × 3)3
Video Lesson

Frequently Asked Questions
What is the cube root of a number?
The cube root of a number is defined as the number which results in the original number when it is cubed. For example, for 8, the cube root will be 2 as 2×2×2 = 8.
What is the easiest method to find the cube root of a number?
The cube root of perfect cubes can be easily found out by using prime factorisation method as explained in this lesson.
What is a perfect cube?
A perfect cube is defined as any number which is the cube of an integer.
How to know if a number is a perfect cube?
To check whether a number is a perfect cube, factorise the number first. If the factors of the number can be equally grouped in triples, the number is a perfect cube.
Learn with us and download the BYJU’S App to have personalised videos based on various Maths concepts and have fun learning.


Sir , How do you find the the first group 375 in cube root as 5
Please teach me the trick to find out cube root of 4
I don’t understand how it is done
What is the cuberoot of 23