In Calculus, the Quotient Rule is a method for determining the derivative (differentiation) of a function in the form of the ratio of two differentiable functions. It is a formal rule used in the differentiation problems in which one function is divided by the other function. The quotient rule follows the definition of the limit of the derivative. Remember that the quotient rule begins with the bottom function and ends with the bottom function squared. In this article, you will look at the definition, quotient rule formula, proof, and examples in detail.
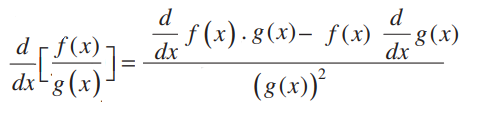
Now, let’s have a look at the definition of quotient rule in differentiation along with the formula.
Quotient Rule Definition
In Calculus, a Quotient rule is similar to the product rule. A Quotient Rule is stated as the ratio of the quantity of the denominator times the derivative of the numerator function minus the numerator times the derivative of the denominator function to the square of the denominator function. In short, the quotient rule is a way of differentiating the division of functions or the quotients. This is also known as the quotient rule differentiation in maths.
Quotient Rule Formula
Let the given function be f(x), which is given by:
\(\begin{array}{l}\large \mathbf{f(x) = \frac{s(x)}{t(x)}}\end{array} \)
Thus, the differentiation of the function is given by:
\(\begin{array}{l}\large \mathbf{f'(x) = \left [ \frac{s(x)}{t(x)} \right ]’ = \frac{t(x).s'(x) – s(x). t'(x)}{\left \{ t(x) \right \}^{2}}}\end{array} \)
The quotient rule of differentiation is defined as the ratio of two functions (1st function / 2nd Function), is equal to the ratio of (Differentiation of 1st function × the 2nd function – Differentiation of second function × the 1st function) to the square of the 2nd function.
Quotient Rule Proof
We know, the derivative of a function is given as:
\(\begin{array}{l}\large \mathbf{f'(x) = \lim \limits_{h \to 0} \frac{f(x+h)- f(x)}{h}}\end{array} \)
Thus, the derivative of ratio of function is:
Hence, the quotient rule is proved.
Quotient Rule Derivative can also be proved using product rule and other differentiation rules as given below.
Suppose the function f(x) is defined as the ratio of two functions, say u(x) and v(x), then it’s derivative can be derived as explained below.
f(x) = u(x)/v(x)
This can also be written as:
f(x) = u(x) [u(x)]-1
Using product rule of differentiation,
f'(x) = u'(x) [v(x)]-1 + u(x) (d/dx) [v(x)]-1
We know that (d/dx)xn = nxn-1,
f'(x) = u'(x) [v(x)]-1 + u(x).(-1)[v(x)]-2 v'(x)
= [u'(x)/v(x)] – [{u(x) v'(x)}/{v(x)}2]
= [u'(x) v(x) – u(x) v'(x)]/ [v(x)]2
This is also called the quotient rule of u and v.
Thus, the above formula can be written as:
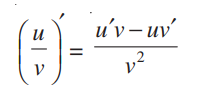
Quotient Rule Example
Let us work out some examples:
Example 1:
Find the derivative of tan x.
Solution:
We know, \(\begin{array}{l}\tan x = \frac{\sin x}{\cos x}\end{array} \)
\(\begin{array}{l}\left (\tan x \right )’ = \frac{\mathrm{d} }{\mathrm{d} x} \left (\frac{\sin x}{\cos x} \right )\end{array} \)
\(\begin{array}{l}= \left ( \frac{\cos x . (\sin x)’ – \sin x (\cos x)’}{\cos^{2}x} \right )\end{array} \)
\(\begin{array}{l}= \left ( \frac{\cos^{2} x + \sin^{2} x }{\cos^{2}x} \right )\end{array} \)
\(\begin{array}{l}= \left ( \frac{1}{\cos^{2}x} \right )\end{array} \)
\(\begin{array}{l}= \sec^{2} x\end{array} \)
Example 2:
\(\begin{array}{l}\text{Find the derivative of }\sqrt{\frac{5x + 7}{3x – 2}}\end{array} \)
Solution:
\(\begin{array}{l}\sqrt{\frac{5x + 7}{3x – 2}} = \frac{\sqrt{5x + 7}}{\sqrt{3x – 2}}\end{array} \)
Applying the quotient rule, we have
\(\begin{array}{l}\frac{\mathrm{d} }{\mathrm{d} x}\left (\sqrt{\frac{5x + 7}{3x – 2}} \right ) = \frac{\sqrt{3x – 2}. \frac{\mathrm{d} }{\mathrm{d} x}\left (\sqrt{5x + 7} \right ) – \sqrt{5x + 7} . \frac{\mathrm{d} }{\mathrm{d} x} \sqrt{3x – 2} }{3x – 2}\end{array} \)
\(\begin{array}{l}= \frac{\sqrt{3x – 2}. \left (\frac{5}{2.\sqrt{5x + 7}} \right ) – \sqrt{5x + 7} . \left (\frac{3}{2.\sqrt{3x – 2}} \right ) }{3x – 2}\end{array} \)
\(\begin{array}{l}= \frac{\left (\frac{5.\sqrt{3x – 2}}{2.\sqrt{5x + 7}} \right ) – \left (\frac{3. \sqrt{5x + 7}}{2.\sqrt{3x – 2}} \right ) }{3x – 2}\end{array} \)
Taking LCM, we have
\(\begin{array}{l}= \frac{5.\left (3x – 2 \right ) – 3. \left (5x + 7 \right )}{2\left (3x – 2 \right )\left ( \sqrt{3x – 2} \right )\left ( \sqrt{5x + 7} \right )}\end{array} \)
\(\begin{array}{l}= \frac{15x – 10 – 15x – 21}{2 \left (3x – 2 \right )^{\frac{3}{2}}\left ( 5x + 7 \right )^{\frac{1}{2}}}\end{array} \)
\(\begin{array}{l}= \frac{-31}{2 \left (3x – 2 \right )^{\frac{3}{2}}\left ( 5x + 7 \right )^{\frac{1}{2}}}\end{array} \)
Example 3:
\(\begin{array}{l}\text{Find the derivative of }\frac{(x+3)^{4}}{\sqrt{x^{2}+5}}\end{array} \)
Solution:
Applying quotient rule, we have
\(\begin{array}{l}\frac{\mathrm{d} }{\mathrm{d} x}\left (\frac{(x+3)^{4}}{\sqrt{x^{2}+5}} \right ) = \frac{\sqrt{x^{2}+5}.\frac{\mathrm{d} }{\mathrm{d} x}(x+3)^{4} – (x+3)^{4} . \frac{\mathrm{d} }{\mathrm{d} x} \left (\sqrt{x^{2}+5} \right )}{x^{2}+5}\end{array} \)
\(\begin{array}{l}= \frac{\sqrt{x^{2}+5}.4(x+3)^{3} – (x+3)^{4} . \frac{2x}{2\sqrt{x^{2}+5}} }{x^{2}+5}\end{array} \)
\(\begin{array}{l}= \frac{4. \left (x^{2}+5 \right ).(x+3)^{3} – x.(x+3)^{4} }{\left (x^{2}+5 \right )^{\frac{3}{2}}}\end{array} \)
\(\begin{array}{l}= \frac{\left ( x+3 \right )^{3}\left [ 4. \left (x^{2}+5 \right ) – x.(x+3) \right ]}{\left (x^{2}+5 \right )^{\frac{3}{2}}}\end{array} \)
\(\begin{array}{l}= \frac{\left ( x+3 \right )^{3}\left [ 4x^{2} + 20 – x^{2} – 3x \right ]}{\left (x^{2}+5 \right )^{\frac{3}{2}}}\end{array} \)
\(\begin{array}{l}= \frac{\left ( x+3 \right )^{3}\left [ 3x^{2} -3x + 20 \right ]}{\left (x^{2}+5 \right )^{\frac{3}{2}}}\end{array} \)
Practice Problems
Practice the questions given below to understand the quotient rule effectively.
- Find the derivative of f(x) = (x + 2)/(3x).
- Find the derivative of the function f(x) = (2x + 3)/(x – 3).
- Derive the formula for derivative of cot x using quotient rule.
- Find the derivative of f(x) = (x + cos x)/tan x
To learn more about the topics like Product Rule, Calculus, Differentiation and Integration, visit BYJU’S – The Learning App and Watch engaging videos.
Frequently Asked Questions – FAQs
Q1
How do you use the quotient rule to differentiate?
We can use the quotient rule to differentiate the given function by converting it into the ratio of two functions. Then we can apply the formula of the quotient rule.
Q2
What is the quotient rule in math?
The quotient rule is a formal rule for differentiating problems where one function is divided by another.
Q3
How do you find the derivative of a division function?
We can find the derivative of a division function by applying the quotient rule of differentiation formula.
Q4
What is the formula of Quotient rule?
The formula of quotient rule for the function f(x) = u(x)/v(x) is given by:
f'(x) = [u'(x) v(x) – u(x) v'(x)]/ [v(x)]^2
Q5
What is the derivative of (x – 1)/2x?
Given function is in quotient form, so let us assume u(x) = x – 1 and v(x) = 2x.
Now, by quotient rule, the derivative of the given function becomes,
(d/dx) [u(x)/v(x)] = [u'(x) v(x) – u(x) v'(x)]/ [v(x)]^2
= [1(2x) – (x – 1)(2)]/(2x)^2
= (2x – 2x + 1)/4x^2
= 1/4x^2



Comments