Differential calculus deals with the rate of change of one quantity with respect to another. Or you can consider it as a study of rates of change of quantities. For example, velocity is the rate of change of distance with respect to time in a particular direction. If f(x) is a function, then f'(x) = dy/dx is the differential equation, where f’(x) is the derivative of the function, y is dependent variable and x is an independent variable.
| f'(x) = dy/dx ; x≠0 |
Calculus Definition
In mathematics, calculus is a branch that deals with finding the different properties of integrals and derivatives of functions. It is based on the summation of the infinitesimal differences. Calculus is the study of continuous change of a function or a rate of change of a function. It has two major branches and those two fields are related to each other by the fundamental theorem of calculus. The two different branches are:
- Differential calculus
- Integral Calculus
In this article, we are going to discuss the differential calculus basics, formulas, and differential calculus examples in detail.
| Also, read: |
Basics of Differential Calculus
In differential calculus basics, you may have learned about differential equations, derivatives, and applications of derivatives. For any given value, the derivative of the function is defined as the rate of change of functions with respect to the given values. Differentiation is a process where we find the derivative of a function. Let us discuss the important terms involved in the differential calculus basics.
Functions
A function is defined as a relation from a set of inputs to the set of outputs in which each input is exactly associated with one output. The function is represented by “f(x)”.
Dependent Variable
The dependent variable is a variable whose value always depends and determined by using the other variable called an independent variable. The dependent variable is also called the outcome variable. The result is being evaluated from the mathematical expression using an independent variable is called a dependent variable.
Independent Variable
Independent variables are the inputs to the functions that define the quantity which is being manipulated in an experiment. Let us consider an example y= 3x. Here, x is known as the independent variable and y is known as the dependent variable as the value of y is completely dependent on the value of x.
Domain and Range
The domain of a function is simply defined as the input values of a function and range is defined as the output value of a function. Take an example, if f(x) = 3x be a function, the domain values or the input values are {1, 2, 3} then the range of a function is given as
f(1) = 3(1) = 3
f(2) = 3(2) = 6
f(3) = 3(3) = 9
Therefore, the range of the function will be {3, 6, 9}.
Limits
The limit is an important thing in calculus. Limits are used to define the continuity, integrals, and derivatives in the calculus. The limit of a function is defined as follows:
Let us take the function as “f” which is defined on some open interval that contains some numbers, say “a”, except possibly at “a” itself, then the limit of a function f(x) is written as:
It means that the limit f(x) as “x” approaches “a” is “L”
Interval
An interval is defined as the range of numbers that are present between the two given numbers. intervals can be classified into two types namely:
- Open Interval – The open interval is defined as the set of all real numbers x such that a < x < b. It is represented as (a, b)
- Closed Interval – The closed interval is defined as the set of all real numbers x such that a ≤ x and x ≤ b, or more concisely, a ≤ x ≤ b, and it is represented by [a, b]
Derivatives
The fundamental tool of differential calculus is derivative. The derivative is used to show the rate of change. It helps to show the amount by which the function is changing for a given point. The derivative is called a slope. It measures the steepness of the graph of a function. It defines the ratio of the change in the value of a function to the change in the independent variable. The derivative of y with respect to x is expressed by dy/dx.
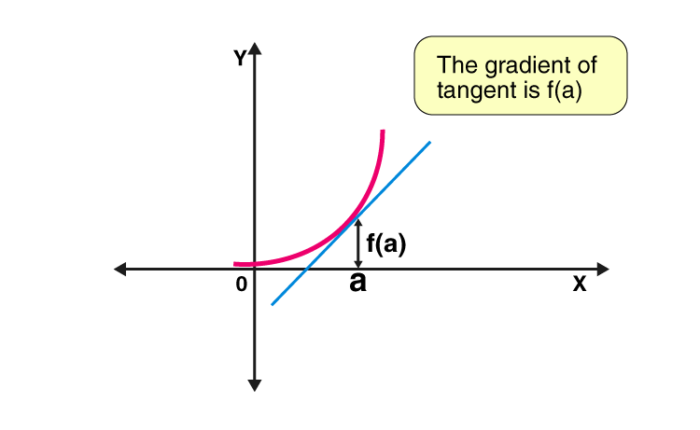
Graphically, we define a derivative as the slope of the tangent, that meets at a point on the curve or which gives derivative at the point where tangent meets the curve. Differentiation has many applications in various fields. Checking the rate of change in temperature of the atmosphere or deriving physics equations based on measurement and units, etc, are the common examples.
Examples
- f(x) = 6x2-2 ⇒ f’(x) = 12x
- f(x) = 2x ⇒ f’(x) = 2
- f(x) = x3 + 2x ⇒ f’(x) = 3x2 + 2
Video Lesson
Differential calculus Questions

Differential Calculus Formulas
How do we study differential calculus? The differentiation is defined as the rate of change of quantities. Therefore, calculus formulas could be derived based on this fact. Here we have provided a detailed explanation of differential calculus which helps users to understand better.
Suppose we have a function f(x), the rate of change of a function with respect to x at a certain point ‘o’ lying in its domain can be written as;
df(x)/dx at point o
Or df/dx at o
So, if y = f(x) is a quantity, then the rate of change of y with respect to x is such that, f'(x) is the derivative of the function f(x). Also, if x and y varies with respect to variable t, then by the chain rule formula, we can write the derivative in the form of differential equations formula as;

Applications
In mathematics, differential calculus is used,
- To find the rate of change of a quantity with respect to other
- In case of finding a function is increasing or decreasing functions in a graph
- To find the maximum and minimum value of a curve
- To find the approximate value of small change in a quantity
Real-life applications of differential calculus are:
- Calculation of profit and loss with respect to business using graphs
- Calculation of the rate of change of the temperature
- Calculation of speed or distance covered such as miles per hour, kilometres per hour, etc.,
- To derive many Physics equations
Problems and Solutions
Go through the given differential calculus examples below:
Example 1: f(x) = 3x2-2x+1
Solution: Given, f(x) = 3x2-2x+1
Differentiating both sides, we get,
f’(x) = 6x – 2, where f’(x) is the derivative of f(x).
Video Lesson on Class 12 Important Calculus Questions


Example 2: f(x) = x3
Solution: We know,
Therefore, f’(x) =
f’(x)= 3 x3-1
f’(x)= 3 x2
Video Lesson

Learn more Maths formulas and problems with us and download BYJU’S – The Learning App for interactive videos.
Frequently Asked Questions – FAQs
What is differential calculus?
Why do we use differential calculus?
To evaluate the approximate value of small change in a quantity
To know if a function is increasing or decreasing functions in a graph
What is the difference between differential calculus and integral calculus?
Integral calculus is a reverse method of finding the derivatives. We deal here with the total size such as area and volumes on a large scale. It is a process of finding antiderivatives.
What are derivatives?
What is the differential equation?
For example, dy/dx=2, where y is the dependent variable and x is the independent variable.

d/dx {k f (x)}=k d/dx g(x)
d/dx(5xpower6)
d/dx(5x^6)
= 5(6)x^(6 – 1) [since d/dx(x^n) = nx^(n-1)]
= 30x^5