NCERT Solutions Class 9 Maths Chapter 9 – Download Free PDF
*According to the latest update on NCERT Syllabus 2023-24, this chapter has been removed.
NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles are valuable resources for exams, as they will help students to score well in the final exams. In order to help students, we have provided detailed chapter-wise solutions to clear their doubts and understanding of the concepts. The NCERT Solutions provided here contain a detailed explanation of all the problems mentioned under Chapter 9 Areas of Parallelograms and Triangles. The NCERT Solutions are created as per the latest syllabus and exam pattern guidelines of the CBSE Board.
Our subject experts have designed these NCERT Solutions for the benefit of students, which cover all the exercise questions from Class 9 Maths NCERT textbook. Students should solve questions from these NCERT Solutions for Class 9, which will help them to prepare well for their exams. Along with the NCERT Solutions, students should also go through other study materials like sample papers, previous year papers, important questions, etc.
NCERT Solutions for Class 9 Maths Chapter 9 – Areas of Parallelograms and Triangles
List of Exercises in Class 9 Maths Chapter 9
Exercise 9.1 Solutions
Access Answers to NCERT Class 9 Maths Chapter 9 – Areas of Parallelograms and Triangles
Exercise 9.1 Page: 155
1. Which of the following figures lie on the same base and in-between the same parallels? In such a case, write the common base and the two parallels.

Solution:
(i) Trapezium ABCD and ΔPDC lie on the same DC and in-between the same parallel lines AB and DC.
(ii) Parallelogram PQRS and trapezium SMNR lie on the same base SR but not in-between the same parallel lines.
(iii) Parallelogram PQRS and ΔRTQ lie on the same base QR and in-between the same parallel lines QR and PS.
(iv) Parallelogram ABCD and ΔPQR do not lie on the same base but in-between the same parallel lines BC and AD.
(v) Quadrilateral ABQD and trapezium APCD lie on the same base AD and in-between the same parallel lines AD and BQ.
(vi) Parallelogram PQRS and parallelogram ABCD do not lie on the same base SR but in-between the same parallel lines SR and PQ.
Exercise 9.2 Page: 159
1. In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Solution:
Given,
AB = CD = 16 cm (Opposite sides of a parallelogram.)
CF = 10 cm and AE = 8 cm
Now,
Area of parallelogram = Base × Altitude
= CD×AE = AD×CF
⇒ 16×8 = AD×10
⇒ AD = 128/10 cm
⇒ AD = 12.8 cm
2. If E, F, G and H are, respectively. the mid-points of the sides of a parallelogram ABCD show that ar (EFGH) = 1/2 ar(ABCD).
Solution:

Given,
E, F, G and H are the mid-points of the sides of a parallelogram ABCD, respectively.
To prove,
ar (EFGH) = ½ ar(ABCD)
Construction,
H and F are joined.
Proof,
AD || BC and AD = BC (Opposite sides of a parallelogram.)
⇒ ½ AD = ½ BC
Also,
AH || BF and and DH || CF
⇒ AH = BF and DH = CF (H and F are mid-points.)
∴, ABFH and HFCD are parallelograms.
Now,
We know that ΔEFH and parallelogram ABFH lie on the same FH, the common base and in-between the same parallel lines AB and HF.
∴ area of EFH = ½ area of ABFH — (i)
And, area of GHF = ½ area of HFCD — (ii)
Adding (i) and (ii),
Area of ΔEFH + area of ΔGHF = ½ area of ABFH + ½ area of HFCD
⇒ area of EFGH = area of ABFH
∴ ar (EFGH) = ½ ar(ABCD)
3. P and Q are any two points lying on the sides DC and AD, respectively, of a parallelogram ABCD.
Show that ar(APB) = ar(BQC).
Solution:

ΔAPB and parallelogram ABCD lie on the same base AB and in-between the same parallel AB and DC.
ar(ΔAPB) = ½ ar(parallelogram ABCD) — (i)
Similarly,
ar(ΔBQC) = ½ ar(parallelogram ABCD) — (ii)
From (i) and (ii), we have
ar(ΔAPB) = ar(ΔBQC)
4. In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = ½ ar(ABCD)
(ii) ar(APD) + ar(PBC) = ar(APB) + ar(PCD)
[Hint: Through P, draw a line parallel to AB.]

Solution:

(i) A line GH is drawn parallel to AB passing through P.
In a parallelogram,
AB || GH (by construction) — (i)
∴,
AD || BC ⇒ AG || BH — (ii)
From equations (i) and (ii),
ABHG is a parallelogram.
Now,
ΔAPB and parallelogram ABHG are lying on the same base AB and in-between the same parallel lines AB and GH.
∴ ar(ΔAPB) = ½ ar(ABHG) — (iii)
also,
ΔPCD and parallelogram CDGH are lying on the same base CD and in-between the same parallel lines CD and GH.
∴ ar(ΔPCD) = ½ ar(CDGH) — (iv)
Adding equations (iii) and (iv),
ar(ΔAPB) + ar(ΔPCD) = ½ [ar(ABHG)+ar(CDGH)]
⇒ ar(APB)+ ar(PCD) = ½ ar(ABCD)
(ii) A line EF is drawn parallel to AD passing through P.
In the parallelogram,
AD || EF (by construction) — (i)
∴,
AB || CD ⇒ AE || DF — (ii)
From equations (i) and (ii),
AEDF is a parallelogram.
Now,
ΔAPD and parallelogram AEFD are lying on the same base AD and in-between the same parallel lines AD and EF.
∴ar(ΔAPD) = ½ ar(AEFD) — (iii)
also,
ΔPBC and parallelogram BCFE are lying on the same base BC and in-between the same parallel lines BC and EF.
∴ar(ΔPBC) = ½ ar(BCFE) — (iv)
Adding equations (iii) and (iv),
ar(ΔAPD)+ ar(ΔPBC) = ½ {ar(AEFD)+ar(BCFE)}
⇒ar(APD)+ar(PBC) = ar(APB)+ar(PCD)
5. In Fig. 9.17, PQRS and ABRS are parallelograms, and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = ½ ar (PQRS)

Solution:
(i) Parallelogram PQRS and ABRS lie on the same base SR and in-between the same parallel lines SR and PB.
∴ ar(PQRS) = ar(ABRS) — (i)
(ii) ΔAXS and parallelogram ABRS are lying on the same base AS and in-between the same parallel lines AS and BR.
∴ ar(ΔAXS) = ½ ar(ABRS) — (ii)
From (i) and (ii), we find that
ar(ΔAXS) = ½ ar(PQRS)
6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts are the fields divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Solution:

The field is divided into three parts, each in a triangular shape.
Let ΔPSA, ΔPAQ and ΔQAR be the triangles.
Area of (ΔPSA + ΔPAQ + ΔQAR) = Area of PQRS — (i)
Area of ΔPAQ = ½ area of PQRS — (ii)
Here, the triangle and parallelogram are on the same base and in-between the same parallel lines.
From (i) and (ii),
Area of ΔPSA +Area of ΔQAR = ½ area of PQRS — (iii)
From (ii) and (iii), we can conclude that
The farmer must sow wheat or pulses in ΔPAQ or either in both ΔPSA and ΔQAR.
Exercise 9.3 Page: 162
1. In Fig.9.23, E is any point on the median AD of a ΔABC. Show that ar (ABE) = ar(ACE).

Solution:
Given,
AD is the median of ΔABC. ∴, it will divide ΔABC into two triangles of equal area.
∴ar(ABD) = ar(ACD) — (i)
also,
ED is the median of ΔABC.
∴ar(EBD) = ar(ECD) — (ii)
Subtracting (ii) from (i),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
⇒ar(ABE) = ar(ACE)
2. In a triangle ABC, E is the mid-point of median AD. Show that ar(BED) = ¼ ar(ABC).
Solution:

ar(BED) = (1/2)×BD×DE
Since E is the mid-point of AD,
AE = DE
Since AD is the median on side BC of triangle ABC,
BD = DC
,
DE = (1/2) AD — (i)
BD = (1/2)BC — (ii)
From (i) and (ii), we get
ar(BED) = (1/2)×(1/2)BC × (1/2)AD
⇒ ar(BED) = (1/2)×(1/2)ar(ABC)
⇒ ar(BED) = ¼ ar(ABC)
3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:

O is the midpoint of AC and BD. (Diagonals bisect each other.)
In ΔABC, BO is the median.
∴ar(AOB) = ar(BOC) — (i)
also,
In ΔBCD, CO is the median.
∴ar(BOC) = ar(COD) — (ii)
In ΔACD, OD is the median.
∴ar(AOD) = ar(COD) — (iii)
In ΔABD, AO is the median.
∴ar(AOD) = ar(AOB) — (iv)
From equations (i), (ii), (iii) and (iv), we get
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
Hence, we get that the diagonals of a parallelogram divide it into four triangles of equal area.
4. In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If the line-segment CD is bisected by AB at O, show that ar(ABC) = ar(ABD).

Solution:
In ΔABC, AO is the median. (CD is bisected by AB at O.)
∴ar(AOC) = ar(AOD) — (i)
also,
ΔBCD, BO is the median. (CD is bisected by AB at O.)
∴ar(BOC) = ar(BOD) — (ii)
Adding (i) and (ii),
We get
ar(AOC)+ar(BOC) = ar(AOD)+ar(BOD)
⇒ar(ABC) = ar(ABD)
5. D, E and F are, respectively, the mid-points of the sides BC, CA and AB of a ΔABC.
Show that
(i) BDEF is a parallelogram.
(ii) ar(DEF) = ¼ ar(ABC)
(iii) ar (BDEF) = ½ ar(ABC)
Solution:

(i) In ΔABC,
EF || BC and EF = ½ BC (by the mid-point theorem.)
also,
BD = ½ BC (D is the mid-point.)
So, BD = EF
also,
BF and DE are parallel and equal to each other.
∴, the pair of opposite sides are equal in length and parallel to each other.
∴ BDEF is a parallelogram.
(ii) Proceeding from the result of (i),
BDEF, DCEF, and AFDE are parallelograms.
A diagonal of a parallelogram divides it into two triangles of equal area.
∴ar(ΔBFD) = ar(ΔDEF) (For parallelogram BDEF) — (i)
also,
ar(ΔAFE) = ar(ΔDEF) (For parallelogram DCEF) — (ii)
ar(ΔCDE) = ar(ΔDEF) (For parallelogram AFDE) — (iii)
From (i), (ii) and (iii)
ar(ΔBFD) = ar(ΔAFE) = ar(ΔCDE) = ar(ΔDEF)
⇒ ar(ΔBFD) +ar(ΔAFE) +ar(ΔCDE) +ar(ΔDEF) = ar(ΔABC)
⇒ 4 ar(ΔDEF) = ar(ΔABC)
⇒ ar(DEF) = ¼ ar(ABC)
(iii) Area (parallelogram BDEF) = ar(ΔDEF) +ar(ΔBDE)
⇒ ar(parallelogram BDEF) = ar(ΔDEF) +ar(ΔDEF)
⇒ ar(parallelogram BDEF) = 2× ar(ΔDEF)
⇒ ar(parallelogram BDEF) = 2× ¼ ar(ΔABC)
⇒ ar(parallelogram BDEF) = ½ ar(ΔABC)
6. In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
If AB = CD, then show that
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

Solution:

Given,
OB = OD and AB = CD
Construction,
DE ⊥ AC and BF ⊥ AC are drawn.
Proof:
(i) In ΔDOE and ΔBOF,
∠DEO = ∠BFO (Perpendiculars)
∠DOE = ∠BOF (Vertically opposite angles)
OD = OB (Given)
∴, ΔDOE ≅ ΔBOF by AAS congruence condition.
∴, DE = BF (By CPCT) — (i)
also, ar(ΔDOE) = ar(ΔBOF) (Congruent triangles) — (ii)
Now,
In ΔDEC and ΔBFA,
∠DEC = ∠BFA (Perpendiculars)
CD = AB (Given)
DE = BF (From i)
∴, ΔDEC ≅ ΔBFA by RHS congruence condition.
∴, ar(ΔDEC) = ar(ΔBFA) (Congruent triangles) — (iii)
Adding (ii) and (iii),
ar(ΔDOE) + ar(ΔDEC) = ar(ΔBOF) + ar(ΔBFA)
⇒ ar (DOC) = ar (AOB)
(ii) ar(ΔDOC) = ar(ΔAOB)
Adding ar(ΔOCB) in LHS and RHS, we get
⇒ar(ΔDOC) + ar(ΔOCB) = ar(ΔAOB) + ar(ΔOCB)
⇒ ar(ΔDCB) = ar(ΔACB)
(iii) When two triangles have same base and equal areas, the triangles will be in between the same parallel lines,
ar(ΔDCB) = ar(ΔACB).
DA || BC — (iv)
For quadrilateral ABCD, one pair of opposite sides are equal (AB = CD), and the other pair of opposite sides are parallel.
∴, ABCD is parallelogram.
7. D and E are points on sides AB and AC, respectively, of ΔABC such that ar(DBC) = ar(EBC). Prove that DE || BC.
Solution:

ΔDBC and ΔEBC are on the same base BC and also have equal areas.
∴, they will lie between the same parallel lines.
∴, DE || BC
8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar(ΔABE) = ar(ΔACF)
Solution:

Given,
XY || BC, BE || AC and CF || AB
To show,
ar(ΔABE) = ar(ΔACF)
Proof:
BCYE is a || gm as ΔABE and ||gm BCYE are on the same base BE and between the same parallel lines BE and AC.
∴,ar(ABE) = ½ ar(BCYE) … (1)
Now,
CF || AB and XY || BC
⇒ CF || AB and XF || BC
⇒ BCFX is a || gm
As ΔACF and || gm BCFX are on the same base CF and in-between the same parallel AB and FC.
∴,ar (ΔACF)= ½ ar (BCFX) … (2)
But,
||gm BCFX and || gm BCYE are on the same base BC and between the same parallels BC and EF.
∴,ar (BCFX) = ar(BCYE) … (3)
From (1), (2) and (3), we get
ar (ΔABE) = ar(ΔACF)
⇒ ar(BEYC) = ar(BXFC)
As the parallelograms are on the same base BC and in-between the same parallels EF and BC–(iii)
Also,
△AEB and ||gm BEYC are on the same base BE and in-between the same parallels BE and AC.
⇒ ar(△AEB) = ½ ar(BEYC) — (iv)
Similarly,
△ACF and || gm BXFC on the same base CF and between the same parallels CF and AB.
⇒ ar(△ ACF) = ½ ar(BXFC) — (v)
From (iii), (iv) and (v),
ar(△ABE) = ar(△ACF)
9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q, and then parallelogram PBQR is completed (see Fig. 9.26). Show that
ar(ABCD) = ar(PBQR).
[Hint: Join AC and PQ. Now compare ar(ACQ) and ar(APQ).]

Solution:

AC and PQ are joined.
Ar(△ACQ) = ar(△APQ) (On the same base AQ and between the same parallel lines AQ and CP)
⇒ ar(△ACQ)-ar(△ABQ) = ar(△APQ)-ar(△ABQ)
⇒ ar(△ABC) = ar(△QBP) — (i)
AC and QP are diagonals ABCD and PBQR.
∴,ar(ABC) = ½ ar(ABCD) — (ii)
ar(QBP) = ½ ar(PBQR) — (iii)
From (ii) and (ii),
½ ar(ABCD) = ½ ar(PBQR)
⇒ ar(ABCD) = ar(PBQR)
10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Solution:

△DAC and △DBC lie on the same base DC and between the same parallels AB and CD.
Ar(△DAC) = ar(△DBC)
⇒ ar(△DAC) – ar(△DOC) = ar(△DBC) – ar(△DOC)
⇒ ar(△AOD) = ar(△BOC)
11. In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that
(i) ar(△ACB) = ar(△ACF)
(ii) ar(AEDF) = ar(ABCDE)

Solution:
- △ACB and △ACF lie on the same base AC and between the same parallels AC and BF.
∴ar(△ACB) = ar(△ ACF)
- ar(△ACB) = ar(△ACF)
⇒ ar(△ACB)+ar(ACDE) = ar(△ACF)+ar(ACDE)
⇒ ar(ABCDE) = ar(AEDF)
12. A villager Itwaari has a plot of land in the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:
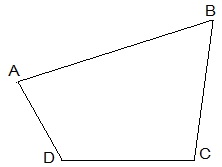
Let ABCD be the plot of the land in the shape of a quadrilateral.
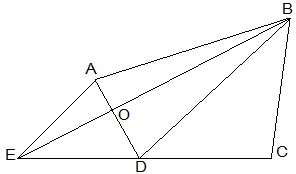
To construct,
Join the diagonal BD.
Draw AE parallel to BD.
Join BE, which intersected AD at O.
We get
△BCE is the shape of the original field.
△AOB is the area for constructing a health centre.
△DEO is the land joined to the plot.
To prove:
ar(△DEO) = ar(△AOB)
Proof:
△DEB and △DAB lie on the same base BD, in-between the same parallels BD and AE.
Ar(△DEB) = ar(△DAB)
⇒ar(△DEB) – ar△DOB) = ar(△DAB) – ar(△DOB)
⇒ ar(△DEO) = ar(△AOB)
13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (△ADX) = ar (△ACY).
[Hint: Join CX.]
Solution:

Given,
ABCD is a trapezium with AB || DC.
XY || AC
Construction,
Join CX
To prove,
ar(ADX) = ar(ACY)
Proof:
ar(△ADX) = ar(△AXC) — (i) (Since they are on the same base AX and in-between the same parallels AB and CD)
Also,
ar(△ AXC)=ar(△ ACY) — (ii) (Since they are on the same base AC and in-between the same parallels XY and AC.)
(i) and (ii),
ar(△ADX) = ar(△ACY)
14. In Fig.9.28, AP || BQ || CR. Prove that ar(△AQC) = ar(△PBR).

Solution:
Given,
AP || BQ || CR
To prove,
ar(AQC) = ar(PBR)
Proof:
ar(△AQB) = ar(△PBQ) — (i) (Since they are on the same base BQ and between the same parallels AP and BQ.)
also,
ar(△BQC) = ar(△BQR) — (ii) (Since they are on the same base BQ and between the same parallels BQ and CR.)
Adding (i) and (ii),
ar(△AQB)+ar(△BQC) = ar(△PBQ)+ar(△BQR)
⇒ ar(△ AQC) = ar(△ PBR)
15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD) = ar(△BOC). Prove that ABCD is a trapezium.
Solution:

Given,
ar(△AOD) = ar(△BOC)
To prove,
ABCD is a trapezium.
Proof:
ar(△AOD) = ar(△BOC)
⇒ ar(△AOD) + ar(△AOB) = ar(△BOC)+ar(△AOB)
⇒ ar(△ADB) = ar(△ACB)
Areas of △ADB and △ACB are equal. ∴, they must lie between the same parallel lines.
∴, AB ∥ CD
∴, ABCD is a trapezium.
16. In Fig.9.29, ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Solution:
Given,
ar(△DRC) = ar(△DPC)
ar(△BDP) = ar(△ARC)
To prove,
ABCD and DCPR are trapeziums.
Proof:
ar(△BDP) = ar(△ARC)
⇒ ar(△BDP) – ar(△DPC) = ar(△DRC)
⇒ ar(△BDC) = ar(△ADC)
∴, ar(△BDC) and ar(△ADC) are lying in-between the same parallel lines.
∴, AB ∥ CD
ABCD is a trapezium.
Similarly,
ar(△DRC) = ar(△DPC).
∴, ar(△DRC) and ar(△DPC) are lying in-between the same parallel lines.
∴, DC ∥ PR
∴, DCPR is a trapezium.
Exercise 9.4(Optional)* Page: 164
1. Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:

Given,
|| gm ABCD and a rectangle ABEF have the same base AB and equal areas.
To prove,
The perimeter of || gm ABCD is greater than the perimeter of rectangle ABEF.
Proof,
We know that the opposite sides of a|| gm and rectangle are equal.
, AB = DC [As ABCD is a || gm]
and, AB = EF [As ABEF is a rectangle]
, DC = EF … (i)
Adding AB on both sides, we get
⇒AB + DC = AB + EF … (ii)
We know that the perpendicular segment is the shortest of all the segments that can be drawn to a given line from a point not lying on it.
, BE < BC and AF < AD
⇒ BC > BE and AD > AF
⇒ BC+AD > BE+AF … (iii)
Adding (ii) and (iii), we get
AB+DC+BC+AD > AB+EF+BE+AF
⇒ AB+BC+CD+DA > AB+ BE+EF+FA
⇒ perimeter of || gm ABCD > perimeter of rectangle ABEF.
The perimeter of the parallelogram is greater than that of the rectangle.
Hence, proved.
2. In Fig. 9.30, D and E are two points on BC such that BD = DE = EC.
Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles – ABD, ADE and AEC – of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide DABC into n triangles of equal areas.]

Solution:
Given,
BD = DE = EC
To prove,
ar (△ABD) = ar (△ADE) = ar (△AEC)
Proof,
In (△ABE), AD is median [since, BD = DE, given]
We know that the median of a triangle divides it into two parts of equal areas.
, ar(△ABD) = ar(△AED) —(i)
Similarly,
In (△ADC), AE is median [Since DE = EC is given]
,ar(ADE) = ar(AEC) —(ii)
From the equation (i) and (ii), we get
ar(ABD) = ar(ADE) = ar(AEC)
3. In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

Solution:
Given,
ABCD, DCFE and ABFE are parallelograms
To prove,
ar (△ADE) = ar (△BCF)
Proof,
In △ADE and △BCF,
AD = BC [Since they are the opposite sides of the parallelogram ABCD.]
DE = CF [Since they are the opposite sides of the parallelogram DCFE.]
AE = BF [Since they are the opposite sides of the parallelogram ABFE.]
, △ADE ≅ △BCF [Using the SSS Congruence theorem.]
, ar(△ADE) = ar(△BCF) [ By CPCT]
4. In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersects DC at P, show that ar (BPC) = ar (DPQ).
[Hint: Join AC.]

Solution:
Given:
ABCD is a parallelogram
AD = CQ
To prove:
ar (△BPC) = ar (△DPQ)
Proof:
In △ADP and △QCP,
∠APD = ∠QPC [Vertically Opposite Angles]
∠ADP = ∠QCP [Alternate Angles]
AD = CQ [given]
, △ABO ≅ △ACD [AAS congruency]
, DP = CP [CPCT]
In △CDQ, QP is median. [Since, DP = CP]
The median of a triangle divides it into two parts of equal areas.
, ar(△DPQ) = ar(△QPC) —(i)
In △PBQ, PC is the median. [Since, AD = CQ and AD = BC ⇒ BC = QC]
The median of a triangle divides it into two parts of equal areas.
, ar(△QPC) = ar(△BPC) —(ii)
From the equation (i) and (ii), we get
ar(△BPC) = ar(△DPQ)
5. In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

(i) ar (BDE) =1/4 ar (ABC)
(ii) ar (BDE) = ½ ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
Solution:
(i) Assume that G and H are the mid-points of the sides AB and AC, respectively.
Join the mid-points with line-segment GH. Here, GH is parallel to third side.
BC will be half of the length of BC by the mid-point theorem.

∴ GH =1/2 BC and GH || BD
∴ GH = BD = DC and GH || BD (D is the mid-point of BC)
Similarly,
GD = HC = HA
HD = AG = BG
ΔABC is divided into 4 equal equilateral triangles ΔBGD, ΔAGH, ΔDHC and ΔGHD
We can say that
ΔBGD = ¼ ΔABC
Considering ΔBDG and ΔBDE,
BD = BD (Common base)
Since both triangles are equilateral triangle, we can say that
BG = BE
DG = DE
, ΔBDG ≅ΔBDE [By SSS congruency]
, area (ΔBDG) = area (ΔBDE)
ar (ΔBDE) = ¼ ar (ΔABC)
Hence, proved.
(ii)

ar(ΔBDE) = ar(ΔAED) (Common base DE and DE||AB)
ar(ΔBDE)−ar(ΔFED) = ar(ΔAED)−ar (ΔFED)
ar(ΔBEF) = ar(ΔAFD) …(i)
Now,
ar(ΔABD) = ar(ΔABF)+ar(ΔAFD)
ar(ΔABD) = ar(ΔABF)+ar(ΔBEF) [From equation (i)]
ar(ΔABD) = ar(ΔABE) …(ii)
AD is the median of ΔABC.
ar(ΔABD) = ½ ar (ΔABC)
= (4/2) ar (ΔBDE)
= 2 ar (ΔBDE)…(iii)
From (ii) and (iii), we obtain
2 ar (ΔBDE) = ar (ΔABE)
ar (BDE) = ½ ar (BAE)
Hence, proved.
(iii) ar(ΔABE) = ar(ΔBEC) [Common base BE and BE || AC]
ar(ΔABF) + ar(ΔBEF) = ar(ΔBEC)
From eqn (i), we get,
ar(ΔABF) + ar(ΔAFD) = a(ΔBEC)
ar(ΔABD) = ar(ΔBEC)
½ ar(ΔABC) = ar(ΔBEC)
ar(ΔABC) = 2 ar(ΔBEC)
Hence, proved.
(iv) ΔBDE and ΔAED lie on the same base (DE) and are in-between the parallel lines DE and AB.
∴ar (ΔBDE) = ar (ΔAED)
Subtracting ar(ΔFED) from L.H.S and R.H.S,
We get
∴ar (ΔBDE)−ar (ΔFED) = ar (ΔAED)−ar (ΔFED)
∴ar (ΔBFE) = ar(ΔAFD)
Hence, proved.
(v) Assume that h is the height of vertex E, corresponding to the side BD in ΔBDE.
Also, assume that H is the height of vertex A, corresponding to the side BC in ΔABC.
While solving Question (i),
We saw that
ar (ΔBDE) = ¼ ar (ΔABC)
While solving Question (iv),
We saw that
ar (ΔBFE) = ar (ΔAFD)
∴ar (ΔBFE) = ar (ΔAFD)
= 2 ar (ΔFED)
Hence, ar (ΔBFE) = 2 ar (ΔFED)
Hence, proved.
(vi) ar (ΔAFC) = ar (ΔAFD) + ar(ΔADC)
= 2 ar (ΔFED) + (1/2) ar(ΔABC) [using (v)]
= 2 ar (ΔFED) + ½ [4ar(ΔBDE)] [Using the result of Question (i)]
= 2 ar (ΔFED) +2 ar(ΔBDE)
ΔBDE and ΔAED are on the same base and between same parallels.
= 2 ar (ΔFED) +2 ar (ΔAED)
= 2 ar (ΔFED) +2 [ar (ΔAFD) +ar (ΔFED)]
= 2 ar (ΔFED) +2 ar (ΔAFD) +2 ar (ΔFED) [From question (viii)]
= 4 ar (ΔFED) +4 ar (ΔFED)
⇒ar (ΔAFC) = 8 ar (ΔFED)
⇒ar (ΔFED) = (1/8) ar (ΔAFC)
Hence, proved.
6. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that
ar (APB)×ar (CPD) = ar (APD)×ar (BPC).
[Hint: From A and C, draw perpendiculars to BD.]
Solution:
Given:
The diagonal AC and BD of the quadrilateral ABCD intersect each other at point E.
Construction:
From A, draw AM perpendicular to BD.
From C, draw CN perpendicular to BD.

To prove,
ar(ΔAED) ar(ΔBEC) = ar (ΔABE) ×ar (ΔCDE)
Proof,
ar(ΔABE) = ½ ×BE×AM………….. (i)
ar(ΔAED) = ½ ×DE×AM………….. (ii)
Dividing eq. ii by i , we get

ar(AED)/ar(ABE) = DE/BE…….. (iii)
Similarly,
ar(CDE)/ar(BEC) = DE/BE ……. (iv)
From eq. (iii) and (iv), we get
ar(AED)/ar(ABE) = ar(CDE)/ar(BEC)
, ar(ΔAED)×ar(ΔBEC) = ar(ΔABE)×ar (ΔCDE)
Hence, proved.
7. P and Q are, respectively, the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP. Show that
(i) ar (PRQ) = ½ ar (ARC)
(ii) ar (RQC) = (3/8) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Solution:
(i)

We know that the median divides the triangle into two triangles of equal area.
PC is the median of ABC.
Ar (ΔBPC) = ar (ΔAPC) ……….(i)
RC is the median of APC.
Ar (ΔARC) = ½ ar (ΔAPC) ……….(ii)
PQ is the median of BPC.
Ar (ΔPQC) = ½ ar (ΔBPC) ……….(iii)
From eq. (i) and (iii), we get
ar (ΔPQC) = ½ ar (ΔAPC) ……….(iv)
From eq. (ii) and (iv), we get
ar (ΔPQC) = ar (ΔARC) ……….(v)
P and Q are the mid-points of AB and BC, respectively [given]
PQ||AC
and, PA = ½ AC
Triangles between the same parallel are equal in area, and we get
ar (ΔAPQ) = ar (ΔPQC) ……….(vi)
From eq. (v) and (vi), we obtain
ar (ΔAPQ) = ar (ΔARC) ……….(vii)
R is the mid-point of AP.
, RQ is the median of APQ.
Ar (ΔPRQ) = ½ ar (ΔAPQ) ……….(viii)
From (vii) and (viii), we get
ar (ΔPRQ) = ½ ar (ΔARC)
Hence, proved.
(ii) PQ is the median of ΔBPC.
ar (ΔPQC) = ½ ar (ΔBPC)
= (½) ×(1/2 )ar (ΔABC)
= ¼ ar (ΔABC) ……….(ix)
Also,
ar (ΔPRC) = ½ ar (ΔAPC) [From (iv)]
ar (ΔPRC) = (1/2)×(1/2)ar ( ABC)
= ¼ ar(ΔABC) ……….(x)
Add eq. (ix) and (x), we get
ar (ΔPQC) + ar (ΔPRC) = (1/4)×(1/4)ar (ΔABC)
ar (quad. PQCR) = ¼ ar (ΔABC) ……….(xi)
Subtracting ar (ΔPRQ) from L.H.S and R.H.S,
ar (quad. PQCR)–ar (ΔPRQ) = ½ ar (ΔABC)–ar (ΔPRQ)
ar (ΔRQC) = ½ ar (ΔABC) – ½ ar (ΔARC) [From result (i)]
ar (ΔARC) = ½ ar (ΔABC) –(1/2)×(1/2)ar (ΔAPC)
ar (ΔRQC) = ½ ar (ΔABC) –(1/4)ar (ΔAPC)
ar (ΔRQC) = ½ ar (ΔABC) –(1/4)×(1/2)ar (ΔABC) [ As, PC is median of ΔABC]
ar (ΔRQC) = ½ ar (ΔABC)–(1/8)ar (ΔABC)
ar (ΔRQC) = [(1/2)-(1/8)]ar (ΔABC)
ar (ΔRQC) = (3/8)ar (ΔABC)
(iii) ar (ΔPRQ) = ½ ar (ΔARC) [From result (i)]
2ar (ΔPRQ) = ar (ΔARC) ……………..(xii)
ar (ΔPRQ) = ½ ar (ΔAPQ) [RQ is the median of APQ] ……….(xiii)
But, we know that
ar (ΔAPQ) = ar (ΔPQC) [From the reason mentioned in eq. (vi)] ……….(xiv)
From eq. (xiii) and (xiv), we get
ar (ΔPRQ) = ½ ar (ΔPQC) ……….(xv)
At the same time,
ar (ΔBPQ) = ar (ΔPQC) [PQ is the median of ΔBPC] ……….(xvi)
From eq. (xv) and (xvi), we get
ar (ΔPRQ) = ½ ar (ΔBPQ) ……….(xvii)
From eq. (xii) and (xvii), we get
2×(1/2)ar(ΔBPQ)= ar (ΔARC)
⟹ ar (ΔBPQ) = ar (ΔARC)
Hence, proved.
8. In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB, respectively. Line segment AX ^ DE meets BC at Y. Show that:

(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2ar(MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2ar(FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN)+ar(ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Solution:
(i) We know that each angle of a square is 90°. Hence, ∠ABM = ∠DBC = 90º
∴∠ABM+∠ABC = ∠DBC+∠ABC
∴∠MBC = ∠ABD
In ∆MBC and ∆ABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ∆MBC ≅ ∆ABD (SAS congruency)
(ii) We have
∆MBC ≅ ∆ABD
∴ar (∆MBC) = ar (∆ABD) … (i)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square BDEC)
∴ BD || AX (Two lines perpendicular to same line are parallel to each other.)
∆ABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
Area (∆YXD) = 2 Area (∆MBC) [From equation (i)] … (ii)
(iii) ∆MBC and parallelogram ABMN are lying on the same base MB and between the same parallels MB and NC.
2 ar (∆MBC) = ar (ABMN)
ar (∆YXD) = ar (ABMN) [From equation (ii)] … (iii)
(iv) We know that each angle of a square is 90°.
∴∠FCA = ∠BCE = 90º
∴∠FCA+∠ACB = ∠BCE+∠ACB
∴∠FCB = ∠ACE
In ∆FCB and ∆ACE,
∠FCB = ∠ACE
FC = AC (Sides of square ACFG)
CB = CE (Sides of square BCED)
∆FCB ≅ ∆ACE (SAS congruency)
(v) AX ⊥ DE and CE ⊥ DE (Adjacent sides of square BDEC) [given]
Hence,
CE || AX (Two lines perpendicular to the same line are parallel to each other.)

Consider BACE and parallelogram CYXE.
BACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ar (∆YXE) = 2ar (∆ACE) … (iv)
We had proved that
∴ ∆FCB ≅ ∆ACE
ar (∆FCB) ≅ ar (∆ACE) … (v)
From equations (iv) and (v), we get
ar (CYXE) = 2 ar (∆FCB) … (vi)
(vi) Consider BFCB and parallelogram ACFG.
BFCB and parallelogram ACFG lie on the same base CF and between the same parallels CF and BG.
∴ar (ACFG) = 2 ar (∆FCB)
∴ar (ACFG) = ar (CYXE) [From equation (vi)] … (vii)
(vii) From the figure, we can observe that
ar (BCED) = ar (BYXD)+ar (CYXE)
∴ar (BCED) = ar (ABMN)+ar (ACFG) [From equations (iii) and (vii)]
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 9 |
| CBSE Notes for Class 9 Maths Chapter 9 |
Summary of NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles
Chapter 9 of Class 9 Maths “Areas of Parallelograms and Triangles” comes under the Unit Mensuration, which in total carries 14 marks. From the unit Mensuration, there will be 2 multiple-choice questions of 2 marks, 2 short types questions of 6 marks each and 1 long-type question of 6 marks, which in total makes it 5.
Chapter 9 – Areas of Parallelograms and Triangles covers topics such as Areas of Parallelograms and Triangles, Figures on the Same Base and between the Same Parallels, as well as Triangles on the Same Base and between the Same Parallels.
The ninth chapter of Class 9 Maths talks about Areas of Parallelograms and Triangles, which introduces students to the basic concepts of Areas of Parallelograms and Triangles, Figures on the Same Base and between the Same Parallels, as well as Triangles on the Same Base and between the Same Parallels. For Class 9 students, these topics are pretty complex and require proper explanations to master. So, the NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles exercises will help them to get an idea of the topic and the concepts they cover.
Importance of NCERT Solutions for Class 9 Maths Chapter 9
Maths is incredibly important in our daily lives as we are all surrounded by the laws of mathematics, and without a good understanding of them, one can face significant problems in life. It is a subject that needs lots of practice and knowledge of different formulas to solve different numerical problems. Class 9 students can now upgrade their Maths problem-solving skills by practising questions from NCERT Solutions for Class 9 Maths which is provided here. All the questions have been picked from the NCERT textbook of Class 9 Maths so that students can score well in their exams.
We, at BYJU’S, provide students with solutions to all the exercises from the NCERT textbook as per the prescribed syllabus, created by our subject experts for the benefit of Class 9 students while preparing for their exam. Thus, by reading our NCERT Solutions for Class 9 Maths Chapter 9, students can easily form a clear understanding of these topics by practising them at their own pace.
Subject experts have formulated the solutions in a lucid manner to improve the problem-solving abilities of the students. For a more clear idea about Areas of Parallelograms and Triangles, students can refer to the study materials available at BYJU’S.


































Comments