CBSE Class 10 Maths Chapter 14 Statistics Objective Questions

CBSE Class 10 Maths Chapter 14 Statistics Objective Questions with solutions is a reference material that will help the students to score good marks in the board exam. Students can get the objective questions chapter-wise, which are organised topic-wise in the PDF. Chapter 14 – Statistics deals with a branch of Mathematics that includes data representation in a meaningful way. From this chapter, students can learn the step deviation methods, find the mode and median of grouped data, convert frequency distribution and the relation between mode, mean and median methods, and so on. CBSE Class 10 Maths Chapter 14 – Statistics Objective Questions is a good resource to prepare well and achieve good results in the Class 10 board exams.

Sub-Topics in Chapter 14 Statistics

These CBSE Class 10 Maths Objective Questions from Chapter 14 are organised topic-wise, and students referring to these will be able to score good marks in the board exam. The topics covered are as follows:

14.1 Introduction to Statistics (4 MCQs )

14.2 Graphical Representation of Cumulative Frequency Distribution

14.3 Mean (6 MCQs)

14.4 Median (1 MCQ)

14.5 Mode (4 MCQs)

14.6 Ogives and questions relating to the Relation between Mean, Mode and Median (2 MCQs)

Download CBSE Class 10 Maths Chapter 14 – Statistics Objective Questions Free PDF

Introduction to Statistics

1. Class mark of a class is obtained by using

a. (upper limit – lower limit) / 2

b. (upper limit + lower limit) / 2

c. upper limit – lower limit

d. upper limit + lower limit

Answer: (b) (upper limit + lower limit) / 2

Solution: Class mark is the midpoint of a class interval. Therefore, its formula is given by (upper limit + lower limit) / 2

2. Look at the following table:

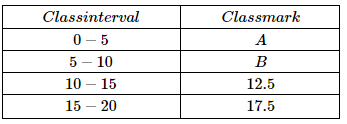
The value of A & B, respectively, are:

a. 3,8

b. 2,7

c. 3,7

d. 2.5, 7.5

Answer: (d) 2.5, 7.5

Solution: Class mark for a class interval = (Upper-class limit + Lower-class limit)/2

For the first class, the upper-class limit is 5, and the lower is 0.

Thus, using the formula, the class mark is 2.5.

For the second class, the upper-class limit is 10, and the lower limit is 5. Thus, the class mark is 7.5.

Hence, the value of A & B, respectively, are 2.5 and 7.5.

3. If the sum of all the frequencies is 24, then the value of z is:

a. 4

b. 6

c. 8

d. 10

Answer: (d) 10

Solution: Here, n=∑fi=z+5+6+1+2=14+z

Given: ∑fi=24

∴ n=∑fi=14+z=24

⇒z=24−14 = 10

Hence, the value of z is 10.

4. The value of ∑ni=1xi is

Mean

5. The mean of the following distribution is

6.

a. 208

b. 444

c. 88

d. 40

Answer: (b) 444

Solution: Each term on the rightmost column is the product of the corresponding 2 terms on the 1^st 2 columns. 1^st column is the class marks list, 2^nd column is the frequencies for these columns, and the 3^rd column is the product of these 2 columns.

For the first row, class mark (x_i) = 4, frequency (f_i) = 10. Product (f_ix_i) = 40. Similarly, the products of other class marks can also be found.

The sum of these products (∑f_ix_i) = 40 + 88 + 108 + 208 = 444.

7. Consider the following distribution of SO2 concentration in the air (in ppm = parts per million) in 30 localities. Find the mean SO2 concentration using the assumed mean method. Also, find the values of A, B and C.

a. -0.04, 0, 0.04, 0.5

b. -0.04, 0, 0.04, 0.6

c. -0.04, 0, 0.04, 0.2

d. -0.04, 0, 0.04, 0.098

Answer: (d) -0.04, 0, 0.04, 0.098

Solution: The 4^th column in the table shown in the question is a table of values of ‘d’.

d_i = x_i – a

Here,

d_i = value of ‘d’ for i^th class mark-row.

x_i = i^th class mark

a = assumed mean value

Applying the given formula for 1^st class interval (0-0.04),

-0.08 = 0.02 – a

a = 0.1

Thus, P = 0.1

Applying the given formula for 2^nd class interval (0.04-0.08),

A = 0.06 – 0.1

A = -0.04

Similarly, for 3^rdand 5^th classes, d values are,

B = 0

C = 0.04

Mean = 0.098

8. There is a grouped data distribution for which the mean is to be found by the step deviation method.

Find the value of A, B, C, D, E and F.

a. 186, -100, -200, -2, -1 and 2

b. 188, -100, 200, -2, -1 and 2

c. 188, 100, -200, 2, -1 and -2

d. 186, 100, -200, -2, -1 and 2

Answer: (b) 188, -100, 200, -2, -1 and 2

Solution: ∑f_i = sum of frequencies of each class = 40 + 39 + 34 + 30 + 45 = 188

d_i = x_i – a

where, x_i = i^th class mark

a = assumed mean

Using the above formula for the 1^st Class (0-100), we get

-200 = 50 – a

a = 250

Using the above formula for the 2^nd Class (100-200), we get

B = 150 – 250

B = -100

Similarly, C = 200.

ui = (d_i)/ h

Here, h = class interval = 100; thus, h is a constant.

For 1^st class (0-100),

u_i = (d_i)/ h= – (200/100) =-2

Thus, D = -2

Similarly E = -1, F = 2

Therefore, A, B, C, D, E and F are 188, -100, 200, -2, -1 and 2, respectively.

9. The formula for finding the mean by the direct method is
Where B and A are, respectively

(A) Class mark, frequency of the class

(B) Average frequency, class size

(C) Class size, average frequency

(D) Frequency of the class, class mark

Answer: (A) Class mark, frequency of the class

Solution:

Where B is the class mark.

Class mark = 1/2 (upper limit of class + lower limit of class)

And, A is the frequency of the class.

10. The average weight of a group of 25 men was calculated to be 78.4 kg. It was discovered later that one weight was wrongly entered as 69 kg instead of 96 kg. What is the correct average?

(A) 75.76

(B) 77.56

(C) 79.48

(B) 80.30

Answer: (C) 79.48

Solution: Total weight of 25 men = 25 × 78.4 = 1960

Due to the error in one entry, 96 has become 69

Difference = 27 kg

∴ Correct total = 1960 + 27 = 1987

∴ Correct average =1987 / 25 = 79.48

Median

11. For arranged data, the median is the 

(A) Most common observation

(B) Middlemost observation

(C) Least common observation

(D) Average of the two most common observations

Answer: (B) Middlemost observation

Solution: The median is the middlemost observation. If there is an even number of observations, the median is the average of the two middle observations. If there is an odd number of observations, the median is the middle observation itself.

Mode

12. The mode of the following data is:

(A) 16

(B) 14

(C) 12

(D) 10

Answer: (B) 14

Solution: The mode is the most frequent observation. Here, the mode is 14 with a frequency of 15.

13.  Find the mode of the following data.

1. Between 20 and 22.5
2. Between 27.5 and 30
3. Equal to 25
4. Between 22.5 and 27.5, but not equal to 25

Answer: (A) Between 20 and 22.5

Solution:

The modal class is 20-30

Mode= l +

= 20 + (14-13) / (28-13-5) × 10 =21

Hence, the mode will be between 20 and 22.5

14. There are lottery tickets labelled with numbers from 1 to 500. I want to find the number which is most common in lottery tickets. What quantity do I need to use?   

(A) Mode

(B) Mean

(C) Median

(D) None of the above

Answer: (A) Mode

Solution: In a distribution, mode gives the data whose frequency is highest. This means that for an ungrouped distribution, the mode is the value of the data that repeats the maximum number of times. For the lottery tickets, I want to find the most repeated number. The mode will serve this purpose.

15.  Which of the following is not a measure of central tendency?

(A) Mode

(B) Range

(C) Median

(D) Mean

Answer: (B) Range

Solution: Three measures of central tendency are mean, median, and mode. Range is a measure of variability or spread of the data.

Ogives and Questions relating to the Relation between Mean, Mode and Median

16. The mode of a frequency distribution can be determined graphically from:

(A) Frequency curve

(B) 0give

(C) Frequency polygon

(D) Histogram

Answer: (B) Ogive

Solution: The mode of a frequency distribution can be determined graphically from the ogive.

17. For ‘more than ogive’, the x-axis represents:

(A) frequency

(B) lower limits of class intervals

(C) mid-values of class-intervals

(D) upper limits of class-intervals

Answer: (B) lower limits of class intervals

Solution: For ‘more than ogive’, the x-axis represents lower limits of class intervals.

From these objective questions from Chapter 14, Statistics, students can find the methods and procedures to solve the questions based on this topic. The solutions are explained in a broad way in these MCQs, such that students can understand the fundamentals quickly and easily.

The extra questions from CBSE Class 10 Maths Chapter 14 are given below for the students to practise.

CBSE Class 10 Maths Chapter 14 Extra Questions

1. Given that the mean of first n natural numbers is 5n/9, then calculate “n”. 
(a) 9
(b) 6
(c) 7
(d) 10

2. If 35 is removed from the data, 30, 34, 35, 36, 37, 38, 39, 40, then how much does the median increase by?
(a) 1
(b) 0.5
(c) 2
(d) 1.5

Stay tuned to BYJU’S for further updates on CBSE study materials. To access interactive Maths and Science Videos, download BYJU’S – The Learning App and subscribe to the YouTube Channel.