*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 9.
NCERT Solutions for Class 9 Maths Chapter 10 Circles are provided here in PDF format, which can be downloaded for free. The NCERT Solutions for the chapter Circles are included as per the latest update of the CBSE curriculum (2023-24) and have been designed by our expert teachers.
Download Exclusively Curated Chapter Notes for Class 9 Maths Chapter – 10 Circles
Download Most Important Questions for Class 9 Maths Chapter – 10 Circles
All the solved questions of Chapter 10 Circles are with respect to the CBSE syllabus and guidelines to help students solve each exercise question present in the book and prepare for the exam. These serve as reference tools for the students to do homework and also support them in scoring good marks. Students can also get the solutions for Class 9th Maths all chapters exercise-wise and practise well for the exams.
NCERT Solutions for Class 9 Maths Chapter 10 – Circles
List of Exercises in Class 9 Maths Chapter 10
Exercise 10.1 Solutions 2 Questions (2 Short)
Exercise 10.2 Solutions 2 Questions (2 long)
Exercise 10.3 Solutions 3 Questions (3 long)
Exercise 10.4 Solutions 6 Questions (6 long)
Exercise 10.5 Solutions 12 Questions (12 long)
Exercise 10.6 Solutions 10 Questions (10 long)
Access Answers of Maths NCERT Class 9 Chapter 10 Circles
Exercise: 10.1 (Page No: 171)
1. Fill in the blanks.
(i) The centre of a circle lies in ____________ of the circle. (exterior/ interior)
(ii) A point whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a _____________ of the circle.
(iv) An arc is a ___________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and _____________ of the circle.
(vi) A circle divides the plane, on which it lies, in _____________ parts.
Solution:
(i) The centre of a circle lies in interior of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle.
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semicircle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in 3 (three) parts.
2. Write True or False. Give reasons for your solutions.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only a finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is the diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution:
(i) True. Any line segment drawn from the centre of the circle to any point on it is the radius of the circle and will be of equal length.
(ii) False. There can be infinite numbers of equal chords in a circle.
(iii) False. For unequal arcs, there can be major and minor arcs. So, equal arcs on a circle cannot be said to be major arcs or minor arcs.
(iv) True. Any chord whose length is twice as long as the radius of the circle always passes through the centre of the circle, and thus, it is known as the diameter of the circle.
(v) False. A sector is a region of a circle between the arc and the two radii of the circle.
(vi) True. A circle is a 2d figure, and it can be drawn on a plane.
Exercise: 10.2 (Page No: 173)
1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution:
To recall, a circle is a collection of points whose every point is equidistant from its centre. So, two circles can be congruent only when the distance of every point of both circles is equal from the centre.

For the second part of the question, it is given that AB = CD, i.e., two equal chords.
Now, it is to be proven that angle AOB is equal to angle COD.
Proof:
Consider the triangles ΔAOB and ΔCOD.
OA = OC and OB = OD (Since they are the radii of the circle.)
AB = CD (As given in the question.)
So, by SSS congruency, ΔAOB ≅ ΔCOD
∴ By CPCT, we have,
∠AOB = ∠COD (Hence, proved).
2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:
Consider the following diagram.

Here, it is given that ∠AOB = ∠COD, i.e., they are equal angles.
Now, we will have to prove that the line segments AB and CD are equal, i.e., AB = CD.
Proof:
In triangles AOB and COD,
∠AOB = ∠COD (As given in the question.)
OA = OC and OB = OD (These are the radii of the circle.)
So, by SAS congruency, ΔAOB ≅ ΔCOD
∴ By the rule of CPCT, we have,
AB = CD (Hence, proved.)
Exercise: 10.3 (Page No: 176)
1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
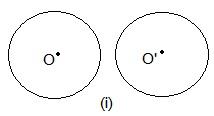
In these two circles, no point is common.
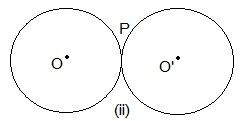
Here, only one point, ‘P’, is common.
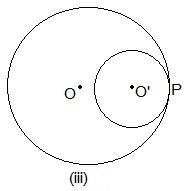
Even here, P is the common point.
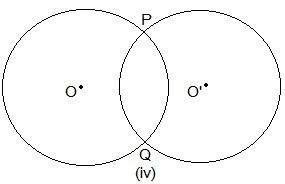
Here, two points are common, which are P and Q.
No point is common in the above circle.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
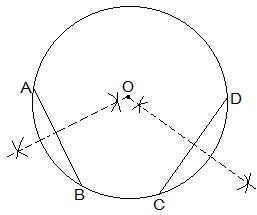
The construction steps to find the centre of the circle is:
Step I: Draw a circle first.
Step II: Draw 2 chords, AB and CD, in the circle.
Step III: Draw the perpendicular bisectors of AB and CD.
Step IV: Connect the two perpendicular bisectors at a point. This intersection point of the two perpendicular bisectors is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
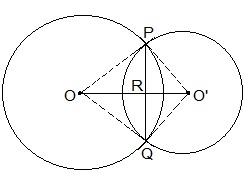
It is given that two circles intersect each other at P and Q.
To prove:
OO’ is perpendicular bisector of PQ.
(i) PR = RQ
(ii) ∠PRO = ∠PRO’ = ∠QRO = ∠QRO’ = 900
Proof:
In triangles ΔPOO’ and ΔQOO’,
OP = OQ and O’P = O’Q (Since they are also the radii.)
OO’ = OO’ (It is the common side.)
So, it can be said that ΔPOO’ ≅ ΔQOO’ (SSS Congruence rule)
∴ ∠POO’ = ∠QOO’ (c.p.c.t)— (i)
Even triangles ΔPOR and ΔQOR are similar by SAS congruency.
OP = OQ (Radii)
∠POR = ∠QOR (As ∠POO’ = ∠QOO’)
OR = OR (Common arm)
So, ΔOPO’ ≅ ΔOQO’ (SAS Congruence rule)
∴ PR = QR and ∠PRO = ∠QRO (c.p.c.t) …. (ii)
As PQ is a line
∠PRO + ∠QRO = 180°
∠PRO + ∠PRO = 180° (Using (ii))
2∠PRO = 180°
∠PRO = 90°
So ∠QRO = ∠PRO = 90°
Here,
∠PRO’ = ∠QRO = 90° and ∠QRO’ = ∠PRO = 90° (Vertically opposite angles)
∠PRO = ∠QRO = ∠PRO’ = ∠QRO’ = 90°
So, OO’ is the perpendicular bisector of PQ.
Exercise: 10.4 (Page No: 179)
1. Two circles of radii 5 cm and 3 cm intersect at two points, and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
The perpendicular bisector of the common chord passes through the centres of both circles.

As the circles intersect at two points, we can construct the above figure.
Consider AB as the common chord and O and O’ as the centres of the circles.
O’A = 5 cm
OA = 3 cm
OO’ = 4 cm [Distance between centres is 4 cm.]
As the radius of the bigger circle is more than the distance between the two centres, we know that the centre of the smaller circle lies inside the bigger circle.
The perpendicular bisector of AB is OO’.
OA = OB = 3 cm
As O is the midpoint of AB
AB = 3 cm + 3 cm = 6 cm
The length of the common chord is 6 cm.
It is clear that the common chord is the diameter of the smaller circle.
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Let AB and CD be two equal cords (i.e., AB = CD). In the above question, it is given that AB and CD intersect at a point, say, E.
It is now to be proven that the line segments AE = DE and CE = BE
Construction Steps
Step 1: From the centre of the circle, draw a perpendicular to AB, i.e., OM ⊥ AB.
Step 2: Similarly, draw ON ⊥ CD.
Step 3: Join OE.
Now, the diagram is as follows:

Proof:
From the diagram, it is seen that OM bisects AB, and so OM ⊥ AB
Similarly, ON bisects CD, and so ON ⊥ CD.
It is known that AB = CD. So,
AM = ND — (i)
and MB = CN — (ii)
Now, triangles ΔOME and ΔONE are similar by RHS congruency, since
∠OME = ∠ONE (They are perpendiculars.)
OE = OE (It is the common side.)
OM = ON (AB and CD are equal, and so they are equidistant from the centre.)
∴ ΔOME ≅ ΔONE
ME = EN (by CPCT) — (iii)
Now, from equations (i) and (ii), we get
AM+ME = ND+EN
So, AE = ED
Now from equations (ii) and (iii), we get
MB-ME = CN-EN
So, EB = CE (Hence, proved)
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
From the question, we know the following:
(i) AB and CD are 2 chords which are intersecting at point E.
(ii) PQ is the diameter of the circle.
(iii) AB = CD.
Now, we will have to prove that ∠BEQ = ∠CEQ
For this, the following construction has to be done.
Construction:
Draw two perpendiculars are drawn as OM ⊥ AB and ON ⊥ D. Now, join OE. The constructed diagram will look as follows:

Now, consider the triangles ΔOEM and ΔOEN.
Here,
(i) OM = ON [The equal chords are always equidistant from the centre.]
(ii) OE = OE [It is the common side.]
(iii) ∠OME = ∠ONE [These are the perpendiculars.]
So, by RHS congruency criterion, ΔOEM ≅ ΔOEN.
Hence, by the CPCT rule, ∠MEO = ∠NEO
∴ ∠BEQ = ∠CEQ (Hence, proved)
4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig. 10.25).

Solution:
The given image is as follows:

First, draw a line segment from O to AD, such that OM ⊥ AD.
So, now OM is bisecting AD since OM ⊥ AD.
Therefore, AM = MD — (i)
Also, since OM ⊥ BC, OM bisects BC.
Therefore, BM = MC — (ii)
From equation (i) and equation (ii),
AM-BM = MD-MC
∴ AB = CD
5. Three girls, Reshma, Salma and Mandip, are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, and Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Solution:

Let the positions of Reshma, Salma and Mandip be represented as A, B and C, respectively.
From the question, we know that AB = BC = 6cm
So, the radius of the circle, i.e., OA = 5cm
Now, draw a perpendicular BM ⊥ AC.
Since AB = BC, ABC can be considered an isosceles triangle. M is the mid-point of AC. BM is the perpendicular bisector of AC, and thus it passes through the centre of the circle.
Now,
let AM = y and
OM = x
So, BM will be = (5-x).
By applying the Pythagorean theorem in ΔOAM, we get
OA2 = OM2 +AM2
⇒ 52 = x2 +y2 — (i)
Again, by applying the Pythagorean theorem in ΔAMB,
AB2 = BM2 +AM2
⇒ 62 = (5-x)2+y2 — (ii)
Subtracting equation (i) from equation (ii), we get
36-25 = (5-x)2 +y2 -x2-y2
Now, solving this equation, we get the value of x as
x = 7/5
Substituting the value of x in equation (i), we get
y2 +(49/25) = 25
⇒ y2 = 25 – (49/25)
Solving it, we get the value of y as
y = 24/5
Thus,
AC = 2×AM
= 2×y
= 2×(24/5) m
AC = 9.6 m
So, the distance between Reshma and Mandip is 9.6 m.
6. A circular park of radius 20m is situated in a colony. Three boys, Ankur, Syed and David, are sitting at equal distances on its boundary, each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
Solution:
First, draw a diagram according to the given statements. The diagram will look as follows:

Here, the positions of Ankur, Syed and David are represented as A, B and C, respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.
AD ⊥ BC is drawn. Now, AD is the median of ΔABC, and it passes through the centre O.
Also, O is the centroid of the ΔABC. OA is the radius of the triangle.
OA = 2/3 AD
Let the side of a triangle a metres, then BD = a/2 m.
Applying Pythagoras’ theorem in ΔABD,
AB2 = BD2+AD2
⇒ AD2 = AB2 -BD2
⇒ AD2 = a2 -(a/2)2
⇒ AD2 = 3a2/4
⇒ AD = √3a/2
OA = 2/3 AD
20 m = 2/3 × √3a/2
a = 20√3 m
So, the length of the string of the toy is 20√3 m.
Exercise: 10.5 (Page No: 184)
1. In Fig. 10.36, A, B and C are three points on a circle with centre O, such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

Solution:
It is given that,
∠AOC = ∠AOB+∠BOC
So, ∠AOC = 60°+30°
∴ ∠AOC = 90°
It is known that an angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So,
∠ADC = (½)∠AOC
= (½)× 90° = 45°
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:

Here, the chord AB is equal to the radius of the circle. In the above diagram, OA and OB are the two radii of the circle.
Now, consider the ΔOAB. Here,
AB = OA = OB = radius of the circle
So, it can be said that ΔOAB has all equal sides, and thus, it is an equilateral triangle.
∴ ∠AOC = 60°
And, ∠ACB = ½ ∠AOB
So, ∠ACB = ½ × 60° = 30°
Now, since ACBD is a cyclic quadrilateral,
∠ADB +∠ACB = 180° (They are the opposite angles of a cyclic quadrilateral)
So, ∠ADB = 180°-30° = 150°
So, the angle subtended by the chord at a point on the minor arc and also at a point on the major arc is 150° and 30°, respectively.
3. In Fig. 10.37, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

Solution:
Since the angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So, the reflex ∠POR = 2×∠PQR
We know the values of angle PQR as 100°.
So, ∠POR = 2×100° = 200°
∴ ∠POR = 360°-200° = 160°
Now, in ΔOPR,
OP and OR are the radii of the circle.
So, OP = OR
Also, ∠OPR = ∠ORP
Now, we know the sum of the angles in a triangle is equal to 180 degrees.
So,
∠POR+∠OPR+∠ORP = 180°
∠OPR+∠OPR = 180°-160°
As ∠OPR = ∠ORP
2∠OPR = 20°
Thus, ∠OPR = 10°
4. In Fig. 10.38, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

Solution:
We know that angles in the segment of the circle are equal, so,
∠BAC = ∠BDC
Now. in the ΔABC, the sum of all the interior angles will be 180°.
So, ∠ABC+∠BAC+∠ACB = 180°
Now, by putting the values,
∠BAC = 180°-69°-31°
So, ∠BAC = 80°
∴ ∠BDC = 80°
5. In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E, such that ∠ BEC = 130° and ∠ ECD = 20°. Find BAC.

Solution:
We know that the angles in the segment of the circle are equal.
So,
∠ BAC = ∠ CDE
Now, by using the exterior angles property of the triangle,
In ΔCDE, we get
∠ CEB = ∠ CDE+∠ DCE
We know that ∠ DCE is equal to 20°.
So, ∠ CDE = 110°
∠ BAC and ∠ CDE are equal
∴ ∠ BAC = 110°
6. ABCD is a cyclic quadrilateral whose diagonals intersect at point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.
Solution:
Consider the following diagram.

Consider the chord CD.
We know that angles in the same segment are equal.
So, ∠ CBD = ∠ CAD
∴ ∠ CAD = 70°
Now, ∠ BAD will be equal to the sum of angles BAC and CAD.
So, ∠ BAD = ∠ BAC+∠ CAD
= 30°+70°
∴ ∠ BAD = 100°
We know that the opposite angles of a cyclic quadrilateral sum up to 180 degrees.
So,
∠ BCD+∠ BAD = 180°
It is known that ∠ BAD = 100°
So, ∠ BCD = 80°
Now, consider the ΔABC.
Here, it is given that AB = BC
Also, ∠ BCA = ∠ CAB (They are the angles opposite to equal sides of a triangle)
∠ BCA = 30°
also, ∠ BCD = 80°
∠ BCA +∠ ACD = 80°
Thus, ∠ ACD = 50° and ∠ ECD = 50°
7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Draw a cyclic quadrilateral ABCD inside a circle with centre O, such that its diagonal AC and BD are two diameters of the circle.

We know that the angles in the semi-circle are equal.
So, ∠ ABC = ∠ BCD = ∠ CDA = ∠ DAB = 90°
So, as each internal angle is 90°, it can be said that the quadrilateral ABCD is a rectangle.
8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:

9. Two circles intersect at two points, B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q, respectively (see Fig. 10.40). Prove that ∠ ACP = ∠ QCD.

Solution:
Construction:
Join the chords AP and DQ.
For chord AP, we know that angles in the same segment are equal.
So, ∠ PBA = ∠ ACP — (i)
Similarly, for chord DQ,
∠ DBQ = ∠ QCD — (ii)
It is known that ABD and PBQ are two line segments which are intersecting at B.
At B, the vertically opposite angles will be equal.
∴ ∠ PBA = ∠ DBQ — (iii)
From equation (i), equation (ii) and equation (iii), we get
∠ ACP = ∠ QCD
10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lies on the third side.
Solution:
First, draw a triangle ABC and then two circles having diameters of AB and AC, respectively.
We will have to now prove that D lies on BC and BDC is a straight line.

Proof:
We know that angles in the semi-circle are equal.
So, ∠ ADB = ∠ ADC = 90°
Hence, ∠ ADB+∠ ADC = 180°
∴ ∠ BDC is a straight line.
So, it can be said that D lies on the line BC.
11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠CBD.
Solution:
We know that AC is the common hypotenuse and ∠ B = ∠ D = 90°.
Now, it has to be proven that ∠ CAD = ∠ CBD

Since ∠ ABC and ∠ ADC are 90°, it can be said that they lie in a semi-circle.
So, triangles ABC and ADC are in the semi-circle, and the points A, B, C and D are concyclic.
Hence, CD is the chord of the circle with centre O.
We know that the angles which are in the same segment of the circle are equal.
∴ ∠ CAD = ∠ CBD
12. Prove that a cyclic parallelogram is a rectangle.
Solution:
It is given that ABCD is a cyclic parallelogram, and we will have to prove that ABCD is a rectangle.

Proof:

Thus, ABCD is a rectangle.
Exercise: 10.6 (Page No: 186)
1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Consider the following diagram.

In ΔPOO’ and ΔQOO’
OP = OQ (Radius of circle 1)
O’P = O’Q (Radius of circle 2)
OO’ = OO’ (Common arm)
So, by SSS congruency, ΔPOO’ ≅ ΔQOO’
Thus, ∠OPO’ = ∠OQO’ (proved).
2. Two chords AB and CD of lengths 5 cm and 11 cm, respectively, of a circle, are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6, find the radius of the circle.
Solution:

Here, OM ⊥ AB and ON ⊥ CD are drawn, and OB and OD are joined.
We know that AB bisects BM as the perpendicular from the centre bisects the chord.
Since AB = 5 so,
BM = AB/2 = 5/2
Similarly, ND = CD/2 = 11/2
Now, let ON be x.
So, OM = 6−x.
Consider ΔMOB,
OB2 = OM2+MB2
Or,

Consider ΔNOD,
OD2 = ON2 + ND2
Or

We know, OB = OD (radii)
From equation 1 and equation 2, we get

Now, from equation (2), we have,
OD2= 12 +(121/4)
Or OD = (5/2)×√5 cm
3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance 4 cm from the centre, what is the distance of the other chord from the centre?
Solution:
Consider the following diagram.

Here, AB and CD are 2 parallel chords. Now, join OB and OD.
Distance of smaller chord AB from the centre of the circle = 4 cm
So, OM = 4 cm
MB = AB/2 = 3 cm
Consider ΔOMB.
OB2 = OM2+MB2
Or, OB = 5cm
Now, consider ΔOND.
OB = OD = 5 (Since they are the radii.)
ND = CD/2 = 4 cm
Now, OD2= ON2+ND2
Or, ON = 3 cm
4. Let the vertex of an angle ABC be located outside a circle, and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Consider the diagram.

Here AD = CE
We know any exterior angle of a triangle is equal to the sum of interior opposite angles.
So,
∠DAE = ∠ABC+∠AEC (in ΔBAE) ——————-(i)
DE subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.
So,
∠DAE = (½)∠DOE ——————-(ii)
Similarly, ∠AEC = (½)∠AOC ——————-(iii)
Now, from equations (i), (ii), and (iii), we get
(½)∠DOE = ∠ABC+(½)∠AOC
Or, ∠ABC = (½)[∠DOE-∠AOC] (Hence, proved)
5. Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution:

To prove: A circle drawn with Q as the centre will pass through A, B and O (i.e., QA = QB = QO).
Since all sides of a rhombus are equal,
AB = DC
Now, multiply (½) on both sides.
(½)AB = (½)DC
So, AQ = DP
BQ = DP
Since Q is the midpoint of AB,
AQ= BQ
Similarly,
RA = SB
Again, as PQ is drawn parallel to AD,
RA = QO
Now, as AQ = BQ and RA = QO, we get
QA = QB = QO (Hence, proved)
6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:

Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
So, ∠AEC+∠CBA = 180°
As ∠AEC and ∠AED are linear pairs,
∠AEC+∠AED = 180°
Or, ∠AED = ∠CBA … (1)
We know in a parallelogram, opposite angles are equal.
So, ∠ADE = ∠CBA … (2)
Now, from equations (1) and (2), we get
∠AED = ∠ADE
Now, AD and AE are angles opposite to equal sides of a triangle.
∴ AD = AE (proved)
7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Solution:

Here, chords AB and CD intersect each other at O.
Consider ΔAOB and ΔCOD.
∠AOB = ∠COD (They are vertically opposite angles.)
OB = OD (Given in the question.)
OA = OC (Given in the question.)
So, by SAS congruency, ΔAOB ≅ ΔCOD
Also, AB = CD (By CPCT)
Similarly, ΔAOD ≅ ΔCOB
Or, AD = CB (By CPCT)
In quadrilateral ACBD, opposite sides are equal.
So, ACBD is a parallelogram.
We know that opposite angles of a parallelogram are equal.
So, ∠A = ∠C
Also, as ABCD is a cyclic quadrilateral,
∠A+∠C = 180°
⇒∠A+∠A = 180°
Or, ∠A = 90°
As ACBD is a parallelogram and one of its interior angles is 90°, so, it is a rectangle.
∠A is the angle subtended by chord BD. And as ∠A = 90°, therefore, BD should be the diameter of the circle. Similarly, AC is the diameter of the circle.
8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F, respectively. Prove that the angles of the triangle DEF are 90°–(½)A, 90°–(½)B and 90°–(½)C.
Solution:
Consider the following diagram.

Here, ABC is inscribed in a circle with centre O, and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F, respectively.
Now, join DE, EF and FD.
As angles in the same segment are equal, so,
∠EDA = ∠FCA ————-(i)
∠FDA = ∠EBA ————-(i)
By adding equations (i) and (ii), we get
∠FDA+∠EDA = ∠FCA+∠EBA
Or, ∠FDE = ∠FCA+∠EBA = (½)∠C+(½)∠B
We know, ∠A +∠B+∠C = 180°
So, ∠FDE = (½)[∠C+∠B] = (½)[180°-∠A]
∠FDE = [90-(∠A/2)]
In a similar way,
∠FED = [90° -(∠B/2)] °
And,
∠EFD = [90° -(∠C/2)] °
9. Two congruent circles intersect each other at points A and B. Through A, any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
The diagram will be

Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)
Now, consider ΔBPQ.
∠APB = ∠AQB
So, the angles are opposite to equal sides of a triangle.
∴ BQ = BP
10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Consider this diagram.

Here, join BE and CE.
Now, since AE is the bisector of ∠BAC,
∠BAE = ∠CAE
Also,
∴arc BE = arc EC
This implies chord BE = chord EC
Now, consider triangles ΔBDE and ΔCDE.
DE = DE (It is the common side)
BD = CD (It is given in the question)
BE = CE (Already proved)
So, by SSS congruency, ΔBDE ≅ ΔCDE.
Thus, ∴∠BDE = ∠CDE
We know, ∠BDE = ∠CDE = 180°
Or, ∠BDE = ∠CDE = 90°
∴ DE ⊥ BC (Hence, proved).
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 10 |
| CBSE Notes for Class 9 Maths Chapter 10 |
Chapter 10, Circles, of Grade 9, is one of the most important chapters, whose concepts will also be used in Class 10. The weightage of this chapter in the final exam is around 15 marks. Therefore, students are advised to read the chapter carefully and practise each and every question included in the textbook with the help of NCERT Solutions, along with examples, to have good practice.
Topics covered in Chapter 10 Circles, are
- Circles and the related terms
- Angle Subtended by a Chord at a Point
- Perpendicular from the Centre to a Chord
- Circle through Three Points
- Equal Chords and Their Distances from the Centre
- Angle Subtended by an Arc of a Circle
- Cyclic Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 10 – Circles are made available for students looking to solve all the problems of Ex-10.1. The methods by which problems have been solved, in a broad way, so that students find it easy to understand the fundamentals of circles. Some of the important points of this chapter are
- A circle is a simple closed geometrical shape equidistant from a central point. It is an important shape in the field of geometry.
- Every circle has its centre.
- The straight line from the centre to the circumference of a circle is called the radius of the circle.
- The length of the line through the centre that touches two points on the edge of the circle is called a diameter.
- The total distance around the circle is called the Circumference.
- The area of the circle can be calculated by applying the formula: A = π r2, where A is the Area, r is the radius, and the value of π is 3.14.
Key Features of NCERT Solutions for Class 9 Maths Chapter 10 – Circles
- The solutions for the chapter Circles work as a reference for the students.
- Students will be able to resolve all the problems of this chapter in a faster way.
- It is good learning material for exam preparation and to do the revision for Class 9 Maths Chapter 10.
- The questions of Circles are solved by our subject experts.
- The NCERT Solutions are given as per the latest update on the CBSE syllabus and guidelines.
Disclaimer:
Dropped Topics – 10.1 Introduction, 10.2 Circles and its related terms: Review and Circle through three points.




































Comments