*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 9.
NCERT Solutions for Class 9 Maths Chapter 10 – Circles Exercise 10.3 have been provided in accordance with the NCERT syllabus and guidelines by CBSE. It has been designed by our expert teachers to make it easier for students to prepare well for the board exam. Students will be able to do their homework with the help of Solutions of Class 9 Maths. Also, it is helpful for students to score good marks in the CBSE exam.
NCERT Solutions for Class 9 Maths Chapter 10 – Circles Exercise 10.3
Access Other Exercise Solutions of Class 9 Maths Chapter 10 – Circles
Exercise 10.1 Solutions 2 Questions ( 2 Short)
Exercise 10.2 Solutions 2 Questions ( 2 long)
Exercise 10.4 Solutions 6 Questions ( 6 long)
Exercise 10.5 Solutions 12 Questions (12 long)
Exercise 10.6 Solutions 10 Questions (10 long)
Access Answers to NCERT Class 9 Maths Chapter 10 – Circles Exercise 10.3
1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
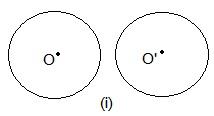
In these two circles, no point is common.
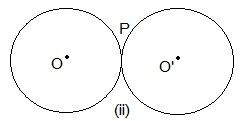
Here, only one point, “P”, is common.
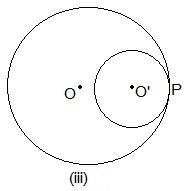
Even here, P is the common point.
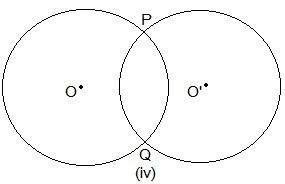
Here, two points are common, which are P and Q.
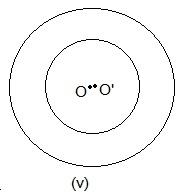
No point is common in the above circle.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
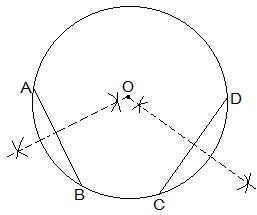
The construction steps to find the centre of the circle are as follows:
Step I: Draw a circle first.
Step II: Draw 2 chords AB and CD in the circle.
Step III: Draw the perpendicular bisectors of AB and CD.
Step IV: Connect the two perpendicular bisectors at a point. This intersection point of the two perpendicular bisectors is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
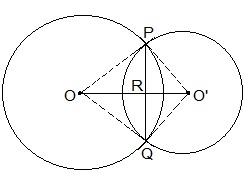
It is given that two circles intersect each other at P and Q.
To prove:
OO’ is a perpendicular bisector of PQ.
(i) PR = RQ
(ii) ∠PRO = ∠PRO’ = ∠QRO = ∠QRO’ = 900
Proof:
In triangles ΔPOO’ and ΔQOO’
OP = OQ and O’P = O’Q (Since they are also the radii)
OO’ = OO’ (It is the common side)
So, it can be said that ΔPOO’ ≅ ΔQOO’ (SSS Congruence rule)
∴ ∠POO’ = ∠QOO’ (c.p.c.t)— (i)
Even triangles ΔPOR and ΔQOR are similar by SAS congruency
OP = OQ (Radii)
∠POR = ∠QOR (As ∠POO’ = ∠QOO’)
OR = OR (Common arm)
So, ΔOPO’ ≅ ΔOQO’ (SAS Congruence rule)
∴ PR = QR and ∠PRO = ∠QRO (c.p.c.t) …. (ii)
As PQ is a line
∠PRO + ∠QRO = 180°
∠PRO + ∠PRO = 180° (Using (ii))
2∠PRO = 180°
∠PRO = 90°
So ∠QRO = ∠PRO = 90°
Here
∠PRO’ = ∠QRO = 90° and ∠QRO’ = ∠PRO = 90° (Vertically opposite angles)
∠PRO = ∠QRO = ∠PRO’ = ∠QRO’ = 90°
So, OO’ is the perpendicular bisector of PQ.
This exercise has three questions based on two topics;
- The perpendicular from the centre to a chord
- Circle through three points
Under these two topics, there are two theorems defined:
Theorem 1: The perpendicular from the centre of a circle to a chord bisects the chord.
Theorem 2: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Practice the Questions for Class 9 Maths Chapter 10 provided by BYJU’S. Students can also reach out to our other learning resources for Class 9, such as notes, question papers, books, etc., provided here. The questions in Ex.10.3 are based on construction for the given condition. Students have to make use of their geometry boxes to solve the problems. To solve each problem mentioned in the textbook, go to NCERT Solutions and get an excellent score in Maths.





Comments