The number system or the numeral system is the system of naming or representing numbers. We know that a number is a mathematical value that helps to count or measure objects and it helps in performing various mathematical calculations. There are different types of number systems in Maths like decimal number system, binary number system, octal number system, and hexadecimal number system. In this article, we are going to learn what is a number system in Maths, different types, and conversion procedures with many number system examples in detail. Also, check mathematics for grade 12 here.
What is Number System in Maths?
A number system is defined as a system of writing to express numbers. It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner. It provides a unique representation of every number and represents the arithmetic and algebraic structure of the figures. It also allows us to operate arithmetic operations like addition, subtraction, multiplication and division.
The value of any digit in a number can be determined by:
- The digit
- Its position in the number
- The base of the number system
Before discussing the different types of number system examples, first, let us discuss what is a number?
What is a Number?
A number is a mathematical value used for counting or measuring or labelling objects. Numbers are used to performing arithmetic calculations. Examples of numbers are natural numbers, whole numbers, rational and irrational numbers, etc. 0 is also a number that represents a null value.
A number has many other variations such as even and odd numbers, prime and composite numbers. Even and odd terms are used when a number is divisible by 2 or not, whereas prime and composite differentiate between the numbers that have only two factors and more than two factors, respectively.
In a number system, these numbers are used as digits. 0 and 1 are the most common digits in the number system, that are used to represent binary numbers. On the other hand, 0 to 9 digits are also used for other number systems. Let us learn here the types of number systems.
Types of Number Systems
There are various types of number systems in mathematics. The four most common number system types are:
- Decimal number system (Base- 10)
- Binary number system (Base- 2)
- Octal number system (Base-8)
- Hexadecimal number system (Base- 16)
Now, let us discuss the different types of number systems with examples.
Decimal Number System (Base 10 Number System)
The decimal number system has a base of 10 because it uses ten digits from 0 to 9. In the decimal number system, the positions successive to the left of the decimal point represent units, tens, hundreds, thousands and so on. This system is expressed in decimal numbers. Every position shows a particular power of the base (10).
Example of Decimal Number System:
The decimal number 1457 consists of the digit 7 in the units position, 5 in the tens place, 4 in the hundreds position, and 1 in the thousands place whose value can be written as:
(1×103) + (4×102) + (5×101) + (7×100)
(1×1000) + (4×100) + (5×10) + (7×1)
1000 + 400 + 50 + 7
1457
Binary Number System (Base 2 Number System)
The base 2 number system is also known as the Binary number system wherein, only two binary digits exist, i.e., 0 and 1. Specifically, the usual base-2 is a radix of 2. The figures described under this system are known as binary numbers which are the combination of 0 and 1. For example, 110101 is a binary number.
We can convert any system into binary and vice versa.
Example
Write (14)10 as a binary number.
Solution:

Base 2 Number System Example
∴ (14)10 = 11102
Octal Number System (Base 8 Number System)
In the octal number system, the base is 8 and it uses numbers from 0 to 7 to represent numbers. Octal numbers are commonly used in computer applications. Converting an octal number to decimal is the same as decimal conversion and is explained below using an example.
Example: Convert 2158 into decimal.
Solution:
2158 = 2 × 82 + 1 × 81 + 5 × 80
= 2 × 64 + 1 × 8 + 5 × 1
= 128 + 8 + 5
= 14110
Hexadecimal Number System (Base 16 Number System)
In the hexadecimal system, numbers are written or represented with base 16. In the hexadecimal system, the numbers are first represented just like in the decimal system, i.e. from 0 to 9. Then, the numbers are represented using the alphabet from A to F. The below-given table shows the representation of numbers in the hexadecimal number system.
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Number System Chart
In the number system chart, the base values and the digits of different number systems can be found. Below is the chart of the numeral system.
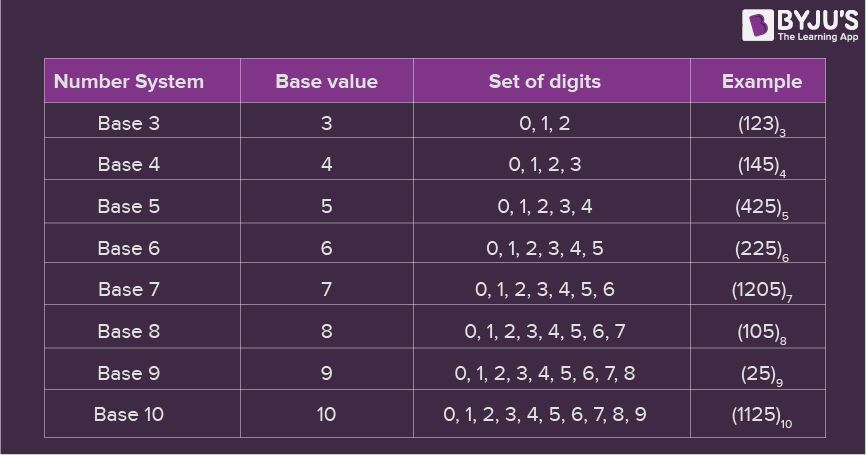
Number System Chart
Number System Conversion
Numbers can be represented in any of the number system categories like binary, decimal, hexadecimal, etc. Also, any number which is represented in any of the number system types can be easily converted to another. Check the detailed lesson on the conversions of number systems to learn how to convert numbers in decimal to binary and vice versa, hexadecimal to binary and vice versa, and octal to binary and vice versa using various examples.
With the help of the different conversion procedures explained above, now let us discuss in brief about the conversion of one number system to the other number system by taking a random number.
Assume the number 349. Thus, the number 349 in different number systems is as follows:
The number 349 in the binary number system is 101011101
The number 349 in the decimal number system is 349.
The number 349 in the octal number system is 535.
The number 349 in the hexadecimal number system is 15D
Number System Solved Examples
Example 1:
Convert (1056)16 to an octal number.
Solution:
Given, 105616 is a hex number.
First we need to convert the given hexadecimal number into decimal number
(1056)16
= 1 × 163 + 0 × 162 + 5 × 161 + 6 × 160
= 4096 + 0 + 80 + 6
= (4182)10
Now we will convert this decimal number to the required octal number by repetitively dividing by 8.
| 8 | 4182 | Remainder |
| 8 | 522 | 6 |
| 8 | 65 | 2 |
| 8 | 8 | 1 |
| 8 | 1 | 0 |
| 0 | 1 |
Therefore, taking the value of the remainder from bottom to top, we get;
(4182)10 = (10126)8
Therefore,
(1056)16 = (10126)8
Example 2:
Convert (1001001100)2 to a decimal number.
Solution:
(1001001100)2
= 1 × 29 + 0 × 28 + 0 × 27 + 1 × 26 + 0 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20
= 512 + 64 + 8 + 4
= (588)10
Example 3:
Convert 101012 into an octal number.
Solution:
Given,
101012 is the binary number
We can write the given binary number as,
010 101
Now as we know, in the octal number system,
010 → 2
101 → 5
Therefore, the required octal number is (25)8
Example 4:
Convert hexadecimal 2C to decimal number.
Solution:
We need to convert 2C16 into binary numbers first.
2C → 00101100
Now convert 001011002 into a decimal number.
101100 = 1 × 25 + 0 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 0 × 20
= 32 + 8 + 4
= 44
Video Lesson on Numeral System

Number System Questions
- Convert (242)10 into hexadecimal. [Answer: (F2)16]
- Convert 0.52 into an octal number. [Answer: 4121]
- Subtract 11012 and 10102. [Answer: 0010]
- Represent 5C6 in decimal. [Answer: 1478]
- Represent binary number 1.1 in decimal. [Answer: 1.5]
Also Check: Binary Operations
Computer Numeral System (Number System in Computers)
When we type any letter or word, the computer translates them into numbers since computers can understand only numbers. A computer can understand only a few symbols called digits and these symbols describe different values depending on the position they hold in the number. In general, the binary number system is used in computers. However, the octal, decimal and hexadecimal systems are also used sometimes.
More Topics Related to Number Systems
| Number System for Class 9 | NCERT Solutions for Class 9 Maths Chapter 1- Number Systems |
| Important Questions Class 9 Maths Chapter 1 Number System | Number System Class 9 Notes – Chapter 1 |
Frequently Asked Questions on Number System
What is Number System and its Types?
The number system is simply a system to represent or express numbers. There are various types of number systems and the most commonly used ones are decimal number system, binary number system, octal number system, and hexadecimal number system.
Why is the Number System Important?
The number system helps to represent numbers in a small symbol set. Computers, in general, use binary numbers 0 and 1 to keep the calculations simple and to keep the amount of necessary circuitry less, which results in the least amount of space, energy consumption and cost.
What is Base 1 Number System Called?
The base 1 number system is called the unary numeral system and is the simplest numeral system to represent natural numbers.


This is wonderfull
i love it
It’s soo helpful and wonderfull
This is very very wonderful.
This is an amazing app
Very helpful 😊👍👍
Very impressive this is.
This is very wonderful app
This app is very helpful for all students and teachers
Very useful it is wonderful app
It’s really help me I m living byjus app
BYJU’S teacher is very intelligent
Very nice
It is very very helpful. It is amazing and wonderful app
I love it it really helped me a lot
I like this site because it’s very amaizing for learning
Excellent job