Natural numbers are a part of the number system which includes all the positive integers from 1 till infinity and are also used for counting purpose. It does not include zero (0). In fact, 1,2,3,4,5,6,7,8,9…., are also called counting numbers.
Natural numbers are part of real numbers, that include only the positive integers i.e. 1, 2, 3, 4,5,6, ………. excluding zero, fractions, decimals and negative numbers.
Note: Natural numbers do not include negative numbers or zero.
In this article, you will learn more about natural numbers with respect to their definition, comparison with whole numbers, representation in the number line, properties, etc.
Natural Number Definition
As explained in the introduction part, natural numbers are the numbers which are positive integers and includes numbers from 1 till infinity(∞). These numbers are countable and are generally used for calculation purpose. The set of natural numbers is represented by the letter “N”.
N = {1,2,3,4,5,6,7,8,9,10…….}
Natural Numbers and Whole Numbers
Natural numbers include all the whole numbers excluding the number 0. In other words, all natural numbers are whole numbers, but all whole numbers are not natural numbers.
- Natural Numbers = {1,2,3,4,5,6,7,8,9,…..}
- Whole Numbers = {0,1,2,3,4,5,7,8,9,….}
Check out the difference between natural and whole numbers to know more about the differentiating properties of these two sets of numbers.
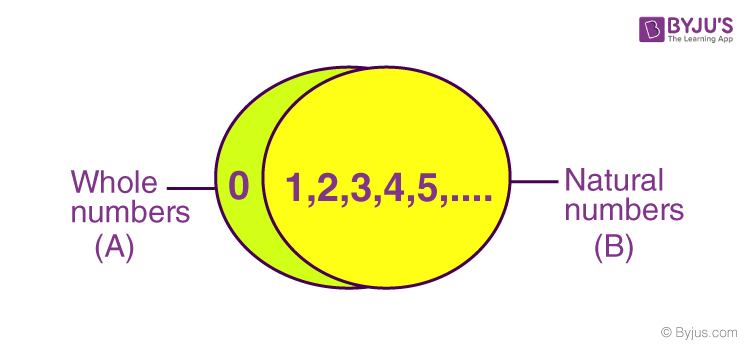
The above representation of sets shows two regions. A ∩ B i.e. intersection of natural numbers and whole numbers (1, 2, 3, 4, 5, 6, ……..) and the green region showing A-B, i.e. part of the whole number (0).
Thus, a whole number is “a part of Integers consisting of all the natural number including 0.”
Is ‘0’ a Natural Number?
The answer to this question is ‘No’. As we know already, natural numbers start with 1 to infinity and are positive integers. But when we combine 0 with a positive integer such as 10, 20, etc. it becomes a natural number. In fact, 0 is a whole number which has a null value.
Every Natural Number is a Whole Number. True or False?
Every natural number is a whole number. The statement is true because natural numbers are the positive integers that start from 1 and goes till infinity whereas whole numbers also include all the positive integers along with 0.
Representing Natural Numbers on a Number Line
Natural numbers representation on a number line is as follows:
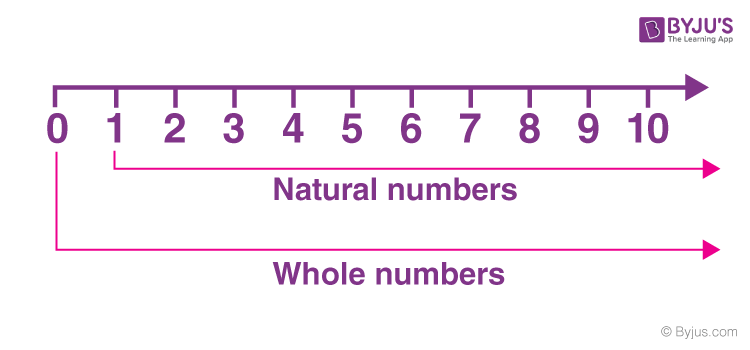
The above number line represents natural numbers and whole numbers. All the integers on the right-hand side of 0 represent the natural numbers, thus forming an infinite set of numbers. When 0 is included, these numbers become whole numbers which are also an infinite set of numbers.
Set of Natural Numbers
In a set notation, the symbol of natural number is “N” and it is represented as given below.
Statement:
N = Set of all numbers starting from 1.
In Roster Form:
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………}
In Set Builder Form:
N = {x : x is an integer starting from 1}
Natural Numbers Examples
The natural numbers include the positive integers (also known as non-negative integers) and a few examples include 1, 2, 3, 4, 5, 6, …∞. In other words, natural numbers are a set of all the whole numbers excluding 0.
23, 56, 78, 999, 100202, etc. are all examples of natural numbers.
Properties of Natural Numbers
Natural numbers properties are segregated into four main properties which include:
- Closure property
- Commutative property
- Associative property
- Distributive property
Each of these properties is explained below in detail.
Closure Property
Natural numbers are always closed under addition and multiplication. The addition and multiplication of two or more natural numbers will always yield a natural number. In the case of subtraction and division, natural numbers do not obey closure property, which means subtracting or dividing two natural numbers might not give a natural number as a result.
- Addition: 1 + 2 = 3, 3 + 4 = 7, etc. In each of these cases, the resulting number is always a natural number.
- Multiplication: 2 × 3 = 6, 5 × 4 = 20, etc. In this case also, the resultant is always a natural number.
- Subtraction: 9 – 5 = 4, 3 – 5 = -2, etc. In this case, the result may or may not be a natural number.
- Division: 10 ÷ 5 = 2, 10 ÷ 3 = 3.33, etc. In this case, also, the resultant number may or may not be a natural number.
Note: Closure property does not hold, if any of the numbers in case of multiplication and division, is not a natural number. But for addition and subtraction, if the result is a positive number, then only closure property exists.
For example:
- -2 x 3 = -6; Not a natural number
- 6/-2 = -3; Not a natural number
Associative Property
The associative property holds true in case of addition and multiplication of natural numbers i.e. a + ( b + c ) = ( a + b ) + c and a × ( b × c ) = ( a × b ) × c. On the other hand, for subtraction and division of natural numbers, the associative property does not hold true. An example of this is given below.
- Addition: a + ( b + c ) = ( a + b ) + c => 3 + (15 + 1 ) = 19 and (3 + 15 ) + 1 = 19.
- Multiplication: a × ( b × c ) = ( a × b ) × c => 3 × (15 × 1 ) = 45 and ( 3 × 15 ) × 1 = 45.
- Subtraction: a – ( b – c ) ≠ ( a – b ) – c => 2 – (15 – 1 ) = – 12 and ( 2 – 15 ) – 1 = – 14.
- Division: a ÷ ( b ÷ c ) ≠ ( a ÷ b ) ÷ c => 2 ÷( 3 ÷ 6 ) = 4 and ( 2 ÷ 3 ) ÷ 6 = 0.11.
Commutative Property
For commutative property
- Addition and multiplication of natural numbers show the commutative property. For example, x + y = y + x and a × b = b × a
- Subtraction and division of natural numbers do not show the commutative property. For example, x – y ≠ y – x and x ÷ y ≠ y ÷ x
Distributive Property
- Multiplication of natural numbers is always distributive over addition. For example, a × (b + c) = ab + ac
- Multiplication of natural numbers is also distributive over subtraction. For example, a × (b – c) = ab – ac
Read More Here:
Operations With Natural Numbers
An overview of algebraic operation with natural numbers i.e. addition, subtraction, multiplication and division, along with their respective properties are summarized in the table given below.
| Properties and Operations on Natural Numbers | |||
|---|---|---|---|
| Operation | Closure Property | Commutative Property | Associative Property |
| Addition | Yes | Yes | Yes |
| Subtraction | No | No | No |
| Multiplication | Yes | Yes | Yes |
| Division | No | No | No |
Video Lesson on Numbers

Solved Examples
Question 1: Sort out the natural numbers from the following list: 20, 1555, 63.99, 5/2, 60, −78, 0, −2, −3/2
Solution: Natural numbers from the above list are 20, 1555 and 60.
Question 2: What are the first 10 natural numbers?
Solution: The first 10 natural numbers on the number line are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Question 3: Is the number 0 a natural number?
Solution: 0 is not a natural number. It is a whole number. Natural numbers only include positive integers.
Stay tuned with BYJU’S and keep learning various other Maths topics in a simple and easily understandable way. Also, get other maths study materials, video lessons, practice questions, etc. by registering at BYJU’S.
Frequently Asked Questions on Natural Numbers
What are Natural Numbers?
Natural numbers are the positive integers or non-negative integers which start from 1 and ends at infinity, such as:
1,2,3,4,5,6,7,8,9,10,……,∞.
Is 0 a Natural Number?
Zero does not have a positive or negative value. Since all the natural numbers are positive integers, hence we cannot say zero is a natural number. Although zero is called a whole number.
What are the first ten Natural Numbers?
The first ten natural numbers are: 1,2,3,4,5,6,7,8,9, and 10.
What is the difference between Natural numbers and Whole numbers?
Natural numbers include only positive integers and starts from 1 till infinity. Whereas whole numbers are the combination of zero and natural numbers, as it starts from 0 and ends at infinite value.
What are the examples of Natural numbers?
The examples of natural numbers are 5, 7, 21, 24, 99, 101, etc.


I like your answers for my mathematics Project Work