Consistent And Inconsistent Systems

A pair of linear equations in two variables in general can be represented as

We can find the solution to these equations by the graphical or algebraic method.

Consistent System

To sketch the graph of pair of linear equations in two variables, we draw two lines representing the equations. The following cases are possible:

i) If both the lines intersect at a point, then there exists a unique solution to the pair of linear equations. In such a case, the pair of linear equations is said to be consistent.

In the graph given above, lines intersect at point P(x, y)  which represents the unique solution of the system of linear equations in two variables.

ii) Consider two lines having equation to be-

Let these lines coincide with each other, then there exist infinitely many solutions since a line consists of infinite points. In such a case, the pair of linear equations is said to be dependent and consistent. As represented in the graph below, the pair of lines coincide and, therefore, dependent and consistent.

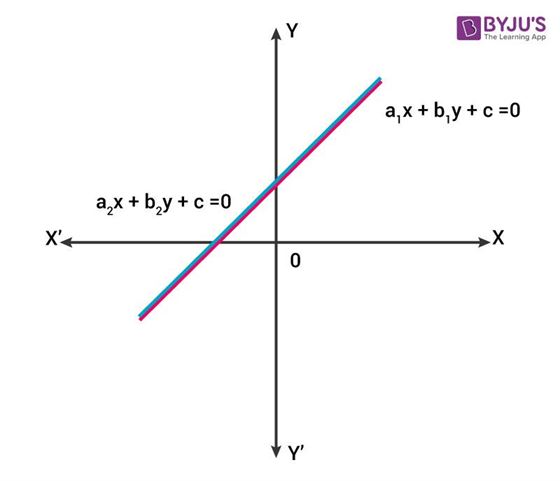
Algebraically, when a₁/a₂ = b₁/b₂ = c₁/c₂,  then the lines coincide and the pair of equations is dependent and consistent.

Inconsistent System

i) Consider the equation of the lines to be-

Let both the lines to be parallel to each other, then there exists no solution because the lines never intersect.

Algebraically, for such a case, a₁/a₂ = b₁/b₂ ≠ c₁/c₂, and the pair of linear equations in two variables is said to be inconsistent.

As shown in the graph above, the pair of lines  a₁x +b₁y +c₁ =0 and a₂x +b₂y +c₁ =0 are parallel to each other.

Therefore, there exists no solution for such a pair.

Solved Example

Check for the consistency of the following pair of linear equations-

Solution:

To check the condition of consistency we need to find out the ratios of the coefficients of the given equations,

Thus,

So, we can say that the above equations represent lines which are coincident in nature and the pair of equations is dependent and consistent.

Therefore, we can say that the lines coincide with each other, having an infinite number of solutions.

Also, when we plot the given equations on a graph, it represents a pair of coincident lines.

Learning is an unending process. Unravel the mysteries of Mathematics with us, and study more by downloading BYJU’S – The Learning App or by visiting our site.