An algebraic equation can be defined as a mathematical statement in which two expressions are set equal to each other. The algebraic equation usually consists of a variable, coefficients and constants.
Also Check: Algebraic Expressions.
In simple words, equations mean equality i.e. the equal sign. That’s what equations are all about- “equating one quantity with another”.
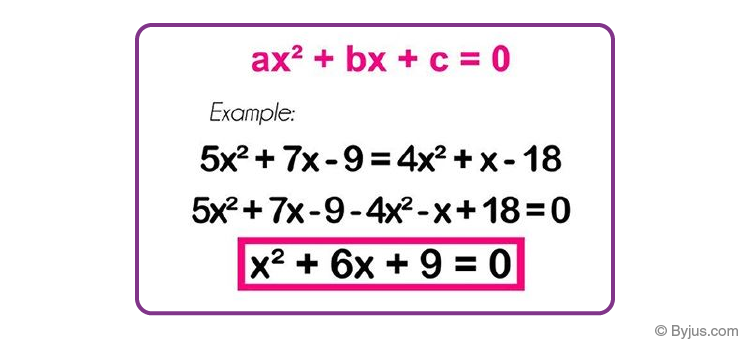
Algebraic Equations
Equations are like a balance scale. If you’ve seen a balance scale, you would know that an equal amount of weight has to be placed on either side for the scale to be considered “balanced”. If we add some weight to just one side, the scale will tip on one side and the two sides are no longer in balance. Equations follow the same logic. Whatever is on one side of the equal sign must have exactly the same value on the other side else it becomes an inequality.
| Table of contents: |
What are Algebraic Equations?
An algebraic equation is an equation in the form:
P = 0
Where P is a polynomial.
For example, x + 8 = 0 is an algebraic equation, where x + 8 is a polynomial. Hence, it is also called a polynomial equation.
An algebraic equation is always a balanced equation that includes variables, coefficients, and constants.
Consider an equation 1+1 = 2.
It is balanced as both sides have the same value. To avoid committing an error that tips the equation out of balance, make sure that any change on one side of the equation is reciprocated on the other side. For example, if you want to add a number 5 to one side of the equation you will have to add the same 5 to the other side of the equation i.e.
1 + 1 = 2
1 + 1 + 5 = 2 + 5
The same goes for subtraction, multiplication, and division. As long as you do the same thing to both sides of the equation it will remain balanced.
What is an Equation?
An equation is simply defined as mathematical statements that express the relationship between two values. Usually, the two values are equated by an equal sign in an equation.
For example, 2x+3 = 7 is an equation, where 2x+3 and 7 are equated by equal to “=” sign.
2x+3 is at the Left-hand side of the equation and 7 is at the right-hand side. In this example,
- 2x, 3 and 7 are terms
- x is the variable
- 3 and 7 are the constants
- ‘+’ is the operator
If we write x = 3, then it is also an equation, where we are denoting the value of variable x equal to 3.
Types of Algebraic Equations
Algebraic equations are of various types. A few of the equations in algebra are:
- Polynomial Equations
- Quadratic Equations
- Cubic Equations
- Rational polynomial Equations
- Trigonometric Equations
Polynomial Equations
All the polynomial equations are a part of algebraic equations like the linear equations. To recall, a polynomial equation is an equation consisting of variables, exponents and coefficients.
- Linear equations: ax+b=c (a not equal to 0)
Quadratic Equations
A quadratic equation is a polynomial equation of degree 2 in one variable of type f(x) = ax2 + bx + c.
- Quadratic Equations: ax2+bx+c=0 (a not equal to 0)
Cubic Equations
The cubic polynomials are polynomials with degree 3. All the cubic polynomials are also algebraic equations.
- Cubic Polynomials: ax3+bx2+cx+d=0
Rational Polynomial Equations
- P(x)/Q(x)=0
Trigonometric Equations
All the trigonometric equations are all considered as algebraic functions. For a trigonometry equation, the expression includes the trigonometric functions of a variable.
- Trigonometric Equations: cos2x = 1+4sinx
How to Solve Algebraic Equations
Consider the following situation. I am going on a trip. In one bag I carry some t-shirts, shorts, and towels. A total of 8 items can fit in the bag. So I pack 4 shirts and 2 shorts. How many towels can I now carry?
Consider the number of towels to be ‘x’. Let’s form the equation now.
4 shirts + 2 shorts + ‘x’ towels = 8 clothes
The left-hand side (LHS) of our equation is being compared to the right-hand side (RHS) of the equation.
Now, let’s solve this equation:
4+2+x=8
6+x=8
6+x-6=8−6
x=2
I can carry 2 towels for my trip.
In the same way, what would depict an inequality? Obviously, when the left-hand side is not equal to the right-hand side. How would this happen?
Let’s take the same 6 + x = 8 and change that equal to into a greater than or a lesser than sign. These aren’t equations! Consider some examples to clarify this concept.
x + 2 = 21, xy + 9 = z are equations but 6p > 77 is not.
Learn More: Solving Linear Equations
Solved Examples
Q.1: Simplify the given equation : 2(x+4)+3(x–5)–2y=0
Solution:
Given equation: 2(x+4)+3(x−5)–2y=0
2x+2×4+3x–3×5–2y=0 (Using Distributive property to get rid of parenthesis)
2x+8+3x–15–2y=0 (Simplifying)
5x–2y–7=0 (on further simplifying terms)
Q.2: Solve x + 1 = 9
Solution: Given, x+1 = 9
If we bring 1 from LHS to RHS, then the sign of 1 will get change.
x = 9 – 1
x = 8
Hence, is the solution.
Q.3: Solve 15 + 5x = 0.
Solution: Given, 15 + 5x = 0
We need to solve for x here.
Let the term with x remain on the LHS and move the rest terms to the RHS.
5x = 0 – 15
5x = -15
Now divide both the sides by 5.
(5x)/5 = -15/5
x = -3
Thus, x = -3 is the required solution.
Q.4: Solve -10x – 19 = 19 – 8x
Solution: Given,-10x – 19 = 19 – 8x is the algebraic equation.
We need to solve the given equation for x.
First write the terms with x on one side and other terms on the other side. Thus, we will add 8x to both the sides
-10 x -19 + 8x = 19 – 8x + 8x
Now group the like terms.
-10x + 8x – 19 = 19
-2x – 19 = 19
Now add 19 both the sides.
-2x – 19 + 19 = 19 + 19
-2x = 38
Divide both sides by 2
(-2x)/2 = 38/2
-x = 19
Multiply both sides by -1
-x (-1) = 19 (-1)
x = -19
Therefore, x = -19 is the required solution.
Related Articles
| Linear Equations | Algebra: Expressions And Equations |
| Math Equations | Algebra Formulas |
Frequently Asked Questions – FAQs
What are algebraic Equations?
What are the basics of algebra?
Is 10 an algebraic expression?
How to Simplify Algebraic equations?
Remove the brackets or parentheses () and multiply the factors
Combine the like terms and simplify them by adding or subtracting
Combine the constants and simplify them by adding or subtracting
What are the basic rules of algebra?
Commutative law ⇒ [x+y = y+x and x.y = y.x] Associative law ⇒ [x+(y+z) = (x+y)+z and x.(y.z) = (x.y).z] Distributive law ⇒ [x.(y+z) = x.y + x.z]


thanks for the wonderful lessons