Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here as variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.

What is an Algebraic Expression?
An algebraic expression in mathematics is an expression which is made up of variables and constants, along with algebraic operations (addition, subtraction, etc.). Expressions are made up of terms. Also, solve questions in Algebraic Expressions Worksheets, at BYJU’S.
Examples
3x + 4y – 7, 4x – 10, etc.
These expressions are represented with the help of unknown variables, constants and coefficients. The combination of these three (as terms) is said to be an expression. It is to be noted that, unlike the algebraic equation, an algebraic expression has no sides or equal to sign. Some of its examples include
- 3x + 2y – 5
- x – 20
- 2x2 − 3xy + 5
Check: Mathematics Grade 12
Variables, Coefficient & Constant in Algebraic Expressions
In Algebra we work with Variable, Symbols or Letters whose value is unknown to us.
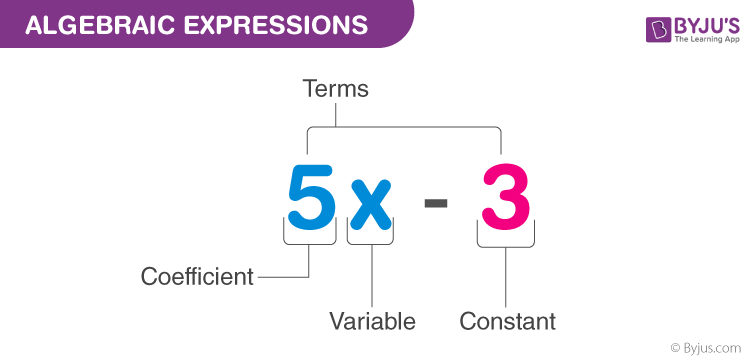
In the above expression (i.e. 5x – 3),
- x is a variable, whose value is unknown to us which can take any value.
- 5 is known as the coefficient of x, as it is a constant value used with the variable term and is well defined.
- 3 is the constant value term that has a definite value.
The whole expression is known to be the Binomial term, as it has two unlikely terms.
Types of Algebraic expression
There are 3 main types of algebraic expressions which include:
- Monomial Expression
- Binomial Expression
- Polynomial Expression
Monomial Expression
An algebraic expression which is having only one term is known as a monomial.
Examples of monomial expressions include 3x4, 3xy, 3x, 8y, etc.
Binomial Expression
A binomial expression is an algebraic expression which is having two terms, which are unlike.
Examples of binomial include 5xy + 8, xyz + x3, etc.
Polynomial Expression
In general, an expression with more than one term with non-negative integral exponents of a variable is known as a polynomial.
Examples of polynomial expression include ax + by + ca, x3 + 2x + 3, etc.
Other Types of Expression
Apart from monomial, binomial and polynomial types of expressions, an algebraic expression can also be classified into two additional types which are:
- Numeric Expression
- Variable Expression
Numeric Expression
A numeric expression consists of numbers and operations, but never include any variable. Some of the examples of numeric expressions are 10 + 5, 15 ÷ 2, etc.
Variable Expression
A variable expression is an expression that contains variables along with numbers and operation to define an expression. A few examples of a variable expression include 4x + y, 5ab + 33, etc.
Algebraic Expression for Class 7
In Class 7, students will come across the terms of algebraic equations such as:
- Coefficient of a term
- Variables
- Constant
- Factors of a term
- Terms of equations
- Like and Unlike terms
Examples of using these terms are given below.
If 2x2+3xy+4x+7 is an algebraic expression.
Then, 2x2, 3xy, 4x and 7 are the terms
Coefficient of term x2 = 2
Constant term = 7
Example of like and unlike terms:
Like terms: 2x and 3x
Unlike terms: 2x and 3y
Factors of a term:
If 3xy is a term, then its factors are 3, x and y.
Monomial, Binomial & Trinomial
Also, in grade 7 we will learn about types of expressions, such as monomial, binomial and trinomial. Let us see examples of each.
Monomial: 2x
Binomial: 2x+3y
Trinomial: 2x+3y+9
Addition and Subtraction of Algebraic Expressions
We can add and subtract like terms easily.
Example: Add 3x + 5y – 6z and x – 4y + 2z.
By adding both the expressions we get;
(3x + 5y – 6z) + (x – 4y + 2z)
Separating the like terms and adding them together:
(3x + x) + (5y – 4y) + (-6z + 2z)
4x + y – 4z
Also, read:
Formulas
The general algebraic formulas we use to solve the expressions or equations are:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a2 – b2 = (a – b)(a + b)
- (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
- a3 – b3 = (a – b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 – ab + b2)
Solved Problem on Algebraic Expression
| Example: Simplify the given expressions by combining the like terms and write the type of Algebraic expression.
(i) 3xy3 + 9x2 y3 + 5y3x (ii) 7ab2 c2 + 2a3 b2 − 3abc – 5ab2 c2 – 2b2 a3 + 2ab (iii) 50x3 – 20x + 8x + 21x3 – 3x + 15x – 41x3 Solution: Creating a table to find the solution:
|
Frequently Asked Questions on Algebraic Expression
How to derive algebraic expressions?
An algebraic expression is a combination of constants, variables and algebraic operations (+, -, ×, ÷). We can derive the algebraic expression for a given situation or condition by using these combinations.
For example, Sima age is thrice more than Tina. And the total age of Sima and Tina is 40. Expressing the algebraic form of this condition;
3x + x = 40 ⇒ 4x = 40; where x is the age of Tina.
Are algebraic expressions polynomials?
No, not all algebraic expressions are polynomials. But all polynomials are algebraic expressions. The difference is polynomials include only variables and coefficients with mathematical operations(+, -, ×) but algebraic expressions include irrational numbers in the powers as well.
Also, polynomials are continuous function (eg: x2 + 2x + 1) but algebraic expression may not be continuous sometimes (eg: 1/x2 – 1 is not continuous at 1).
Is 4 an algebraic expression?
No, 4 is not an algebraic expression because an expression should have at least one variable and one operation to be algebraic.
What are all the types of algebraic expressions?
There are three basic types of algebraic expressions. They are;
- Monomial-Which has only one non-zero term.
- Binomial-Which has two non-zero terms.
- Polynomial- Which has more than one non-zero term with non-negative integral exponents.


Hi…thanks…this has been so helpful!
Hi this is so helpfull for me
pls give me some exercises on these
thank you please continue your good deeds 🙂
If 4 is a constant polynomial(degree zero) and all polynomials are algebraic expressions, doesn’t that mean 4 is an algebraic expression?
A constant polynomial like 4 can be written as 4x^0 which is an algebraic expression
Thnks for ur nice explaination. This helps me very much.
All concepts are very very useful and crystal clear.
conceptully cleared !!!!
What is the correct expression for the data given in this table listed below?
A B
1 10
2 14
3 18
4 22
B=4A+6
Thank you really helpfull
4 is an algebraic expression called constant algebraic expression because 4 can be written as 4 with any variable whose power is 0 and anything raised to power 0 is 1 .
Secondly even 4 can be written as 4 + 0 or 4 -0 since it includes operator.
what is the formula of a set and quadratic equations
Please visit: https://byjus.com/jee/quadratic-equations/
4 is an algebraic expression called constant algebraic expression because 4 can be written as 4 with any variable whose power is 0 and anything raised to power 0 is 1 .
Secondly even 4 can be written as 4 + 0 or 4 -0 since it includes operator.
Under which type of algebraic expression would the expression 5(x+5) fall?
5x+25 is a binomial expression.
Yes it is binomial expression since there are 2 terms which are unlike 5x and +25
X+Y-XY IS WHICH TYPE OF EXPRESSION?
X+Y-XY is a trinomial, as it has three terms in it (X,Y,-XY).
Now I understand thank you very much
I purple you💜💜