Vectors

Vectors, in Maths, are objects which have both, magnitude and direction. Magnitude defines the size of the vector. It is represented by a line with an arrow, where the length of the line is the magnitude of the vector and the arrow shows the direction. It is also known as Euclidean vector or Geometric vector or Spatial vector or simply “vector“. 

Two vectors are said to equal if their magnitude and direction are the same. It plays an important role in Mathematics, Physics as well as in Engineering. According to vector algebra, a vector can be added to another vector, head to tail. The order of addition of two vectors does not matter, because the result will be the same. Check laws of vector addition for more details.

Vectors Definition

The vectors are defined as an object containing both magnitude and direction. Vector describes the movement of an object from one point to another.  Vector math can be geometrically picturised by the directed line segment.

The length of the segment of the directed line is called the magnitude of a vector and the angle at which the vector is inclined shows the direction of the vector. The starting point of a vector is called “Tail” and the ending point (having an arrow) is called “Head.”

A vector is defined as a mathematical structure. It has many applications in the field of physics and geometry. We know that the location of the points on the coordinate plane can be represented using the ordered pair such as (x, y). The usage of the vector is very useful in the simplification process of three-dimensional geometry.

Along with the term vector, we have heard the term scalar. A scalar actually represents the “real numbers”. In simpler words, a vector of “n” dimensions is an ordered collection of n elements called “components“.

Examples of Vectors

The most common examples of the vector are Velocity, Acceleration, Force, Increase/Decrease in Temperature etc. All these quantities have directions and magnitude both. Therefore, it is necessary to calculate them in their vector form.

Also, speed is a quantity that has magnitude but no direction. This is the basic difference between speed and velocity.

Vector Notation

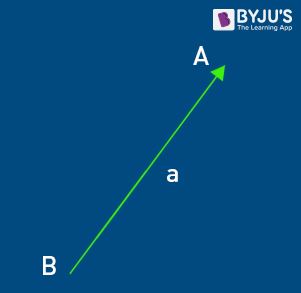
As we know already, a vector has both magnitude and direction. In the above figure, the length of the line AB is the magnitude and head of the arrow points towards the direction.

Magnitude of a Vector

The magnitude of a vector is shown by vertical lines on both the sides of the given vector “|a|”. It represents the length of the vector. Mathematically, the magnitude of a vector is calculated by the help of “Pythagoras Theorem,” i.e.

|a|= √(x²+y²)

Unit Vector

A unit vector has a length (or magnitude) equal to one, which is basically used to show the direction of any vector. A unit vector is equal to the ratio of a vector and its magnitude. Symbolically, it is represented by a cap or hat (^). 

If a is vector of arbitrary length and its magnitude is ||a||, then the unit vector is given by:

It is also known as normalising a vector.

Zero Vector

A vector with zero magnitudes is called a zero vector. The coordinates of zero vector are given by (0,0,0) and it is usually represented by 0 with an arrow (→) at the top or just 0. 

The sum of any vector with zero vector is equal to the vector itself, i.e., if ‘a’ is any vector, then;

0+a = a

Note: There is no unit vector for zero vector and it cannot be normalised.

Operations on Vectors

In maths, we have learned the different operations we perform on numbers. Let us learn here the vector operation such as Addition, Subtraction, Multiplication on vectors.

Addition of Vectors

The two vectors a and b can be added giving the sum to be a + b. This requires joining them head to tail.

We can translate the vector b till its tail meets the head of a. The line segment that is directed from the tail of vector a to the head of vector b is the vector “a + b”.

Characteristics of Vector Math Addition

• Commutative Law- the order of addition does not matter, i.e, a + b = b + a
• Associative law- the sum of three vectors has nothing to do with which pair of the vectors are added at the beginning.

i.e. (a + b) + c = a + (b + c)

Subtraction of Vectors

Before going to the operation it is necessary to know about the reverse vector(-a).

A reverse vector (-a) which is opposite of ‘a’ has a similar magnitude as ‘a’ but pointed in the opposite direction.

First, we find the reverse vector.

Then add them as the usual addition.

Such as if we want to find vector b – a

Then, b – a = b + (-a)

Scalar Multiplication of Vectors

Multiplication of a vector by a scalar quantity is called “Scaling.” In this type of multiplication, only the magnitude of a vector is changed not the direction.

• S(a+b) = Sa + Sb
• (S+T)a = Sa + Ta
• a.1 = a
• a.0 = 0
• a.(-1) = -a

Scalar Triple Product

The scalar triple product, also called a box product or mixed triple product, of three vectors, say a, b and c is given by (a×b)⋅c. Since it involves dot product and evaluates single value, therefore stated as the scalar product. It is also denoted by (a b c). 

(a b c) = (a×b)⋅c

The major application of the scalar triple product can be seen while determining the volume of a parallelepiped, which is equal to the absolute value of |(a×b)⋅c|, where a, b and c are the vectors denoting the sides of parallelepiped respectively. Hence,

Volume of parallelepiped = ∥a×b∥ ∥c∥ |cosϕ|=|(a×b)⋅c|

Vector Multiplication

Basically, there are two types of vector multiplication:

• Cross product
• Dot product

Cross Product of Vectors

The cross product of two vectors results in a vector quantity. It is represented by a cross sign between two vectors.

i.e., a × b

The mathematical value of a cross product-

where,

| a | is the magnitude of vector a.

| b | is the magnitude of vector b.

θ is the angle between two vectors a & b.

Dot product of  Vectors

The dot product of two vectors always results in scalar quantity, i.e. it has only magnitude and no direction. It is represented by a dot (.) in between two vectors.

Components of Vectors (Horizontal & Vertical)

There are two components of a vector in the x-y plane.

1. Horizontal Component
2. Vertical Component

Breaking a vector into its x and y components in the vector space is the most common way for solving vectors.

A vector “a” is inclined with horizontal having an angle equal to θ.

This given vector “a” can be broken down into two components i.e. a_x and a_y.

The component a_x is called a “Horizontal component” whose value is a cos θ.

The component a_y is called a “Vertical component” whose value is a sin θ.

Applications of Vectors

Some of the important applications of vectors in real life are listed below:

• The direction in which the force is applied to move the object can be found using vectors.
• To understand how gravity uses a force of attraction on an object to work.
• The motion of a body which is confined to a plane can be obtained using vectors.
• Vectors help in defining the force applied on a body simultaneously in the three dimensions. 
• Vectors are used in the field of Engineering, where the force is much stronger than the structure will sustain, else it will collapse.
• In various oscillators, vectors are used.
• Vectors also have its applications in ‘Quantum Mechanics’.
• The velocity in a pipe can be determined in terms of the vector field—for example, fluid mechanics.
• We may also observe them everywhere in the general relativity.
• Vectors are used in various wave propagations such as vibration propagation, sound propagation, AC wave propagation, and so on.

Problems and Solutions

Example 1: Given vector V, having a magnitude of 10 units & inclined at 60°. Break down the given vector into its two components.

Solution:

Given, Vector V  having magnitude|V| = 10 units and θ = 60°

Horizontal component (V_x) = V cos θ

V_x = 10 cos 60°

V_x = 10 × 0.5

V_x = 5 units

Now, Vertical component(V_y) = V sin θ

V_y = 10 sin 60°

V_y = 10 × √3/2

V_y = 10√3 units

Example 2:

Find the magnitude of vector a (3,4).

Solution-

Given Vector a = (3,4)

|a|= √(x²+y²)

|a|= √(3²+4²)

|a|= √(9+16) = √25

Therefore, | a |= 5

Example 3:

Find the scalar and vector multiplication of two vectors ‘a’ and ‘b’, given by 3i – 1j + 2k and 1i + -2j + 3k respectively.

Solution-

Given vector a (3,-1,2) and vector b (1,-2,3)

Where θ is the angle between the vectors. But we don’t know the angle between the vectors thus another method of multiplication can be used.

a.b = (3i – 1j + 2k) . (1i -2j +3k)

a.b = 3(i.i) + 2(j.j) + 6(k.k)

a.b = 3 + 2 + 6

a.b = 11

To learn all concepts in Math in a more engaging way, register at BYJU’S. Also, watch interesting videos on various maths topics by downloading BYJU’S– The Learning App.