Scalar Triple Product

By the name itself, it is evident that the scalar triple product of vectors means the product of three vectors. It means taking the dot product of one of the vectors with the cross product of the remaining two. It is denoted as

[a b c ] = ( a × b) . c

The following conclusions can be drawn, by looking into the above formula:

i) The resultant is always a scalar quantity.

ii) Cross product of the vectors is calculated first, followed by the dot product which gives the scalar triple product.

iii) The physical significance of the scalar triple product formula represents the volume of the parallelepiped whose three coterminous edges represent the three vectors a, b and c. The following figure will make this point more clear.

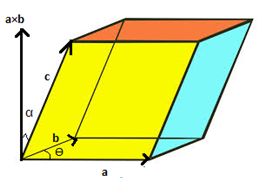
According to this figure, the three vectors are represented by the coterminous edges as shown. The cross product of vectors a and b  gives the area of the base, and also, the direction of the cross product of vectors is perpendicular to both the vectors. As volume is the product of area and height, the height, in this case, is given by the component of vector c along the direction of the cross product of a and b. The component is given by c cos α.

Thus, we can conclude that for a Parallelepiped, if the coterminous edges are denoted by three vectors and a, b and c then,

Volume of parallelepiped = ( a × b) c cos α =  ( a × b) . c

Where α is the angle between  ( a × b)  and c.

We are familiar with the expansion of cross products of vectors. Keeping that in mind, if it is given that

then, we can express the above equation as,

This indicates the dot product of two vectors. Using properties of determinants, we can expand the above equation as,

According to the dot product of vector properties,

Properties of Scalar Triple Product:

i) If the vectors are cyclically permuted, then

( a × b) . c = a.( b × c) 

ii)  The product is cyclic in nature, i.e.,

a.(b × c) = b.(c × a) = c.(a × b)

Thus,

[ a b c ] = [ b c a ] = [ c a b ] = – [ b a c ] = – [ c b a ] = – [ a c b ] 

Example: Three vectors are given by,

By using the scalar triple product of vectors, verify that [a b c ] = [ b c a ] = – [ a c b ] 

Solution: First of all let us find [ a b c ].

[a b c ] = ( a × b ) . c 

⇒ [ a b c ] = 1(-1 – 1) – 1(1 – 2) – 2(1 + 2) = -2 + 1 – 6 = -7

Now let us evaluate [ b c a ] and [ a  c b ] similarly,

= 1(-2 – 1) + 1(-4 – 1) + 1(2 – 1) = -3 – 5 + 1 = -7

= 2(2 – 1) – 1(-2 – 1) + 1(1 + 1) = 2 + 3 + 2 = 7

Hence it can be seen that [ a b c] = [ b c a ] = – [ a c b ] 

Try to recall the properties of determinants since the concept of determinants helps in solving these types of problems easily.

iii) If the triple product of vectors is zero, then it can be inferred that the vectors are coplanar in nature.

The triple product indicates the volume of a parallelepiped. If it is zero, then such a case could only arise when any one of the three vectors is of zero magnitude. The direction of the cross product of a and b is perpendicular to the plane which contains a and b. The dot product of the resultant with c will only be zero if the vector c also lies in the same plane. This is because the angle between the resultant and C will be 90° and cos  90°.

Thus, by the use of the scalar triple product, we can easily find out the volume of a given parallelepiped. There are a lot of real-life applications of vectors which are very interesting to learn. To get more knowledge on vectors, download BYJU’S – The Learning App.