A tangent to a circle is defined as a line that touches the circle exactly at one point. The point at which the tangent touches the circle is called the point of contact. Based on the position of this point, we can define the number tangents than can be drawn to a circle. There are some important points regarding tangents:
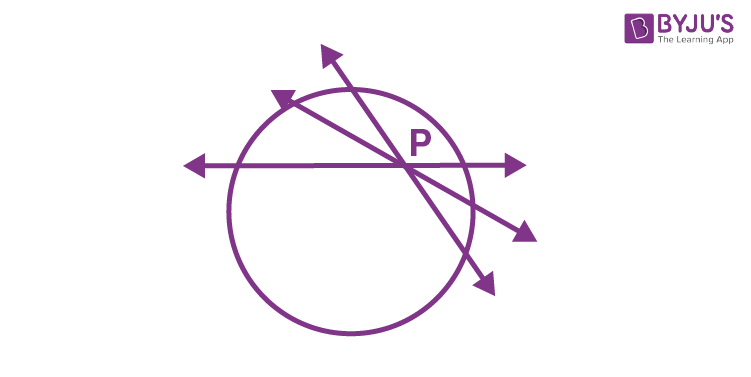
- A tangent to a circle cannot be drawn through a point which lies inside the circle. It is so because all the lines passing through any point inside the circle will intersect the circle at two points. This can be observed in the below figure.
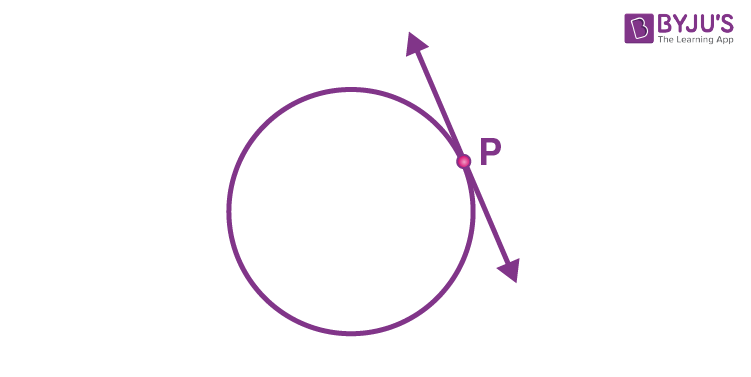
- There is exactly one tangent to a circle which passes through only one point on the circle as shown in the below figure.
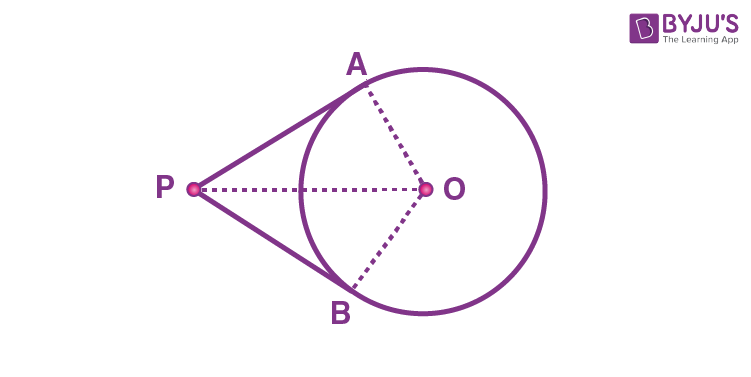
- There are exactly two tangents can be drawn to a circle from a point outside the circle as shown in the following figure.

In the figure, \(\begin{array}{l}P\end{array} \)
is an external point from which tangents are drawn to the circle. \(\begin{array}{l}T_{1}\end{array} \)
and \(\begin{array}{l}T_{2}\end{array} \)
are points of contact of the tangent with a circle. The length of a tangent is equal to the length of a line segment with end-points as the external point and the point of contact. So, \(\begin{array}{l}PT_{1}\end{array} \)
and \(\begin{array}{l}PT_{2}\end{array} \)
are the lengths of tangent to the circle from an external point \(\begin{array}{l}P\end{array} \)
.
Some theorems on length of tangent
Theorem 1: The lengths of tangents drawn from an external point to a circle are equal.
Proof:
Consider the circle with center \(\begin{array}{l}O\end{array} \)
. \(\begin{array}{l}PA\end{array} \)
and \(\begin{array}{l}PB\end{array} \)
are the two tangents drawn to the circle from the external point \(\begin{array}{l}P\end{array} \)
. \(\begin{array}{l}OA\end{array} \)
and \(\begin{array}{l}OB\end{array} \)
are radii of the circle.
Tangent is perpendicular to the radius through the point of contact.
\(\begin{array}{l}∠PAO\end{array} \)
= \(\begin{array}{l}∠PBO\end{array} \)
= \(\begin{array}{l}90°\end{array} \)
Consider the triangles, \(\begin{array}{l}∆PAO\end{array} \)
and \(\begin{array}{l}∆PBO\end{array} \)
,
\(\begin{array}{l}∠PAO\end{array} \)
= \(\begin{array}{l}∠PBO\end{array} \)
= \(\begin{array}{l}90°\end{array} \)
\(\begin{array}{l}PO\end{array} \)
is common side for both the triangles,
\(\begin{array}{l}OA\end{array} \)
= \(\begin{array}{l}OB\end{array} \)
[Radii of the circle]
Hence, by RHS congruence theorem,
\(\begin{array}{l}∆PAO ≅ ∆PBO\end{array} \)
\(\begin{array}{l}⇒ PA = PB\end{array} \)
(Corresponding parts of congruent triangles)
This can also be proved by using Pythagoras theorem as follows,
Since,
\(\begin{array}{l}∠PAO\end{array} \)
= \(\begin{array}{l}∠PBO\end{array} \)
= \(\begin{array}{l}90°\end{array} \)
\(\begin{array}{l}∆PAO\end{array} \)
and \(\begin{array}{l}∆PBO\end{array} \)
are right angled triangles.
\(\begin{array}{l}PA^2\end{array} \)
= \(\begin{array}{l}OP^2 – OA^2\end{array} \)
Since \(\begin{array}{l}OA\end{array} \)
= \(\begin{array}{l}OB\end{array} \)
,
\(\begin{array}{l}PA^2\end{array} \)
= \(\begin{array}{l}OP^2 – OB^2\end{array} \)
= \(\begin{array}{l}PB^2\end{array} \)
This gives, \(\begin{array}{l}PA\end{array} \)
= \(\begin{array}{l}PB\end{array} \)
Therefore, tangents drawn to a circle from an external point have equal lengths.
There is an important observation here:
- Since
\(\begin{array}{l}∠APO\end{array} \)
= \(\begin{array}{l}∠BPO\end{array} \)
, \(\begin{array}{l}OP\end{array} \)
is the angle bisector of \(\begin{array}{l}∠APB\end{array} \)
.
Therefore, the centre of the circle lies on the angle bisector of the angle made by two tangents to the circle from an external point.
Also, read:
Let’s consider an example for better understanding of the concept of length of the tangents drawn to a circle from an external point.
Solved Example
Example: A circle is inscribed in the quadrilateral \(\begin{array}{l}ABCD\end{array} \)
, prove that \(\begin{array}{l}AB + CD\end{array} \)
= \(\begin{array}{l}AD + BC\end{array} \)
.
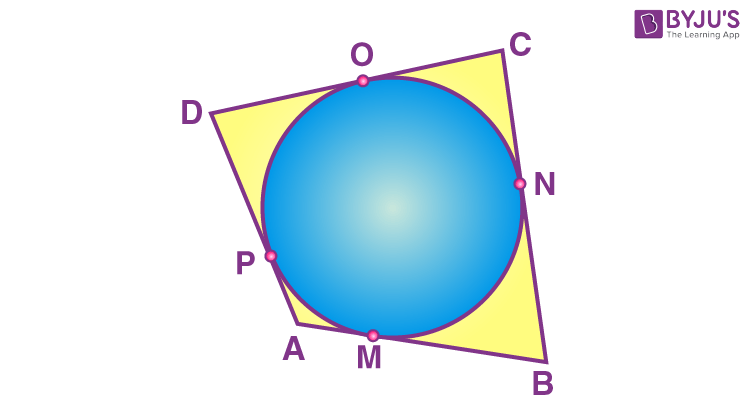
Solution:
We know that the lengths of tangents drawn from an external point to a circle are equal.
Tangents drawn from the point \(\begin{array}{l}A\end{array} \)
will have equal lengths.
\(\begin{array}{l}AP\end{array} \)
= \(\begin{array}{l}AM\end{array} \)
….(1)
Similarly, for tangents drawn from point \(\begin{array}{l}B\end{array} \)
,
\(\begin{array}{l}BN\end{array} \)
= \(\begin{array}{l}BM\end{array} \)
….(2)
Tangents drawn from point \(\begin{array}{l}C\end{array} \)
,
\(\begin{array}{l}CN\end{array} \)
= \(\begin{array}{l}CO\end{array} \)
….(3)
Tangents drawn from point \(\begin{array}{l}D\end{array} \)
,
\(\begin{array}{l}DP\end{array} \)
= \(\begin{array}{l}DO\end{array} \)
….(4)
Adding equations (1),(2), (3) and (4),
\(\begin{array}{l}AP + BN + CN + DP\end{array} \)
= \(\begin{array}{l}AM + BM + CO + DO\end{array} \)
By rearranging the terms,
\(\begin{array}{l}\Rightarrow AP + PD + BN + NC\end{array} \)
= \(\begin{array}{l}AM + MB + CO + OD\end{array} \)
From the given figure,
AM + MB = AB and CO + OD = CD
\(\begin{array}{l}\Rightarrow AD + BC\end{array} \)
= \(\begin{array}{l}AB + CD\end{array} \)
Hence proved.
To know more about the length of a tangent, download BYJU’S – The Learning App today! Also, get the interactive videos on science and maths concepts.






Comments