Like Fractions And Unlike Fractions

A fraction is a number representing a part of a single whole object or a group of objects. It is defined by two numbers, one on top and the other at the bottom of a fraction bar, known as numerator and denominator respectively. Depending upon the similarity of the denominator, we categorize two or more fractions into like fractions and unlike fractions. They are also termed sometimes as a similar fraction and dissimilar fractions.

The meaning of like is same and unlike means different. Now here in this article, we will learn to perform the arithmetic operations on both the type of fractions along with how to convert unlike fraction into a like fraction with examples. Let us learn more here.

Also, read:

Like Fractions

The group of two or more fractions that have exactly the same denominator are called like fractions. Or we can say that the fractions which have the same numbers in the denominators are called like fractions. For example, 1/7, 2/7, 5/7, 6/7  are all like fractions, whose denominators equal to 7.

It is easy to perform arithmetic operations such as addition and subtraction on like fractions. We don’t have to neutralize the denominators while performing both the operations. Let us understand with the help of examples.

Addition and Subtraction of Like Fractions

When we add or subtract the like fractions, the denominator will remain the same and only numerators are added or subtracted respectively. Below are the examples.

Example 1: Add 2/3 and 5/3

Solution: 2/3 + 5/3 = (2+5)/3 = 7/3

Example 2: Subtract 1/2 from 11/2.

Solution: 11/2 – 1/2 = (11-1)/2 = 10/2 = 5

Points to Remember

• 2/4, 4/8, 1/2, etc. are not like fractions, although when simplified, they all result in 1/2.
• 6/16 and 6/26 are not like fractions. The numerators are the same, but denominators are not.
• 2, 3, 4 are like fractions since their denominators are considered as 1, which implies these fractions are 2/1, 3/1 and 4/1.

Unlike Fractions

Fractions with different denominators are called the unlike fractions. Here the denominators of fractions have different values. For example, 2/3, 4/9, 6/67, 9/89 are unlike fractions.

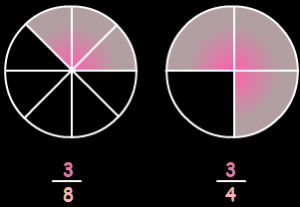
Unlike Fractions

Since the denominators here are different, therefore it is not easy to add or subtract such fractions. To perform arithmetic operations like addition and subtraction, we have to covert the unlike fractions into like fractions first. Then we perform the required operation.

Addition and Subtraction of Unlike Fractions

When we add and subtract two unlike fractions, we have to make the denominator equal first and then perform the respective operation. There are two methods by which we can make the denominator equal. They are:

• Cross-Multiplication Method
• LCM Method

In the cross multiplication method, we cross multiply the numerator of the first fraction by the denominator of the second fraction. Then multiply the numerator of the second fraction by the denominator of the first fraction. Now, multiply both the denominators and take it as a common denominator. Then we can add or subtract the fractions now.

Example: Add 1/3 and 3/4

Solution: 1/3 + 3/4

By cross multiplication method, we get;

=[(1 x 4) + (3 x 3)]/3 x 4

=(4 + 9)/12

=13/12

In the LCM method, first, we need to take the LCM of denominators of the given fractions. Now using this LCM, make all the fractions as like fractions. Then we can simplify the numerator.

Example: Add 3/8 and 5/12

Solution: 3/8 + 5/12

Now take the LCM of 8 and 12, we get;

LCM (8, 12) = 2 x 2 x 2 x 3 = 24

Now multiply the given fractions to get the denominators equal to 24, such that;

=[(3 x 3)/(8 x 3)] + [(5 x 2) + (12 x 2)]

=(9/24) + (10/24)

=(9+10)/24

=19/24.

Conversion of Unlike to Like Fraction

Like fractions facilitate the comparison of fractions. So there is often a need to convert unlike fractions to them.

Let us convert 1, 4/5, 7/10 and 1/2 into like fractions. Steps for conversion:

• Find the LCM of the denominators. LCM of 1, 5, 10 and 2 is 10.
• Calculate their equivalent fractions with the same denominator, that is, the LCM.

1/1 = (1×10)/(1×10) = 10/10

4/5 = (4×2)/(5×2) = 8/10

7/10 = (7×1)/(10×1) = 7/10

1/2 = (1×5)/(2×5) = 5/10

1, 4/5, 7/10 and 1/2 are unlike fractions, which can be represented as 10/10, 8/10, 7/10 and 5/10 which are like fractions.

It is to be noted that when the denominators become equal, the fractions can be compared. You would not be able to answer the largest among 1, 4/5, 7/10 and 1/2. But once they have been converted to 10/10, 8/10, 7/10 and 5/10, you can arrange them in the ascending order of 5/10, 7/10, 8/10 and 10/10 very conveniently.

Types of Fractions

There are majorly three types of fractions, they are:

• Proper Fraction
• Improper Fraction
• Mixed Fraction

Proper and Improper Fractions

Similar to like and unlike fractions, we have another type of fractions, which are known as proper and improper fractions.

• A proper fraction is a fraction that has a value less than 1. Or we can say, when the value of the numerator is less than the denominator, then such fractions are called proper fractions—for example, 1/2, 1/3, 4/5, 6/7, 8/9, etc.
• An improper fraction is a fraction whose value is more than 1. When the value of the numerator is greater than the value of denominator, then the fraction is known as improper fractions. For example, 3/2, 5/4, 4/3. 8/3, etc.

Mixed Fraction

When a number is a combination of a whole number and a proper fraction, then it is called a mixed fraction. For example:

To learn more about fractions, download BYJU’S – The Learning App today!