A polygon is a two-dimensional geometric figure that has a finite number of sides. The sides of a polygon are made of straight line segments connected to each other end to end. Thus, the line segments of a polygon are called sides or edges. The point where two line segments meet is called vertex or corners, henceforth an angle is formed. An example of a polygon is a triangle with three sides. A circle is also a plane figure but it is not considered a polygon, because it is a curved shape and does not have sides or angles. Therefore, we can say, all the polygons are 2d shapes but not all the two-dimensional figures are polygons.

We can observe different types of polygons in our daily existence and we might be using them knowingly or unknowingly. In this article, you will learn the meaning and definition of a polygon, types of a polygon, real-life examples of polygon shapes along with their properties and related formulas in detail.
| Table of Contents: |
What are Polygons?
A Polygon is a closed figure made up of line segments (not curves) in a two-dimensional plane. Polygon is the combination of two words, i.e. poly (means many) and gon (means sides).
A minimum of three line segments is required to connect end to end, to make a closed figure. Thus a polygon with a minimum of three sides is known as Triangle and it is also called 3-gon. An n-sided polygon is called n-gon.
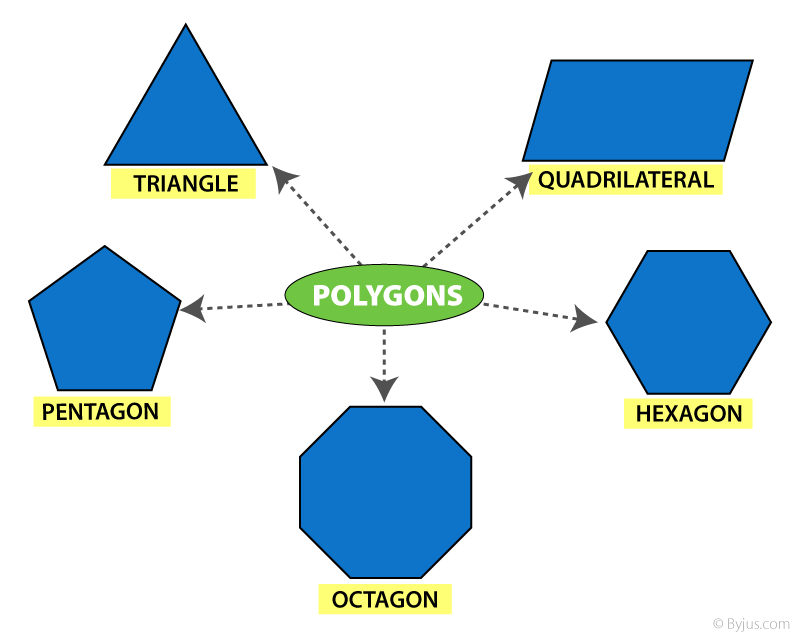
Polygon shape
By definition, we know that the polygon is made up of line segments. Below are the shapes of some polygons that are enclosed by the different number of line segments.
Types of Polygon
Depending on the sides and angles, the polygons are classified into different types, namely:
- Regular Polygon
- Irregular Polygon
- Convex Polygon
- Concave polygon
Regular Polygon
If all the sides and interior angles of the polygon are equal, then it is known as a regular polygon. The examples of regular polygons are square, equilateral triangle, etc.
Irregular Polygon
If all the sides and the interior angles of the polygon are of different measure, then it is known as an irregular polygon. This means that either the sides are of different lengths or the angles are different, which is sufficient for a polygon to be said to be irregular. For example, a scalene triangle, a rectangle, a kite, etc.
Convex Polygon
If all the interior angles of a polygon are strictly less than 180 degrees, then it is known as a convex polygon. The vertex will point outwards from the centre of the shape.
Concave Polygon
If one or more interior angles of a polygon are more than 180 degrees, then it is known as a concave polygon. A concave polygon can have at least four sides. The vertex points towards the inside of the polygon.
However, a number of polygons are defined based on the number of sides, angles and properties.
Angles of Polygon
As we know, any polygon has as many vertices as it has sides. Each corner has a certain measure of angles. These angles are categorized into two types namely interior angles and exterior angles of a polygon.
Interior Angle Property
The sum of all the interior angles of a simple n-gon = (n − 2) × 180°
Or
Sum = (n − 2)π radians
Where ‘n’ is equal to the number of sides of a polygon.
For example, a quadrilateral has four sides, therefore, the sum of all the interior angles is given by:
Sum of interior angles of 4-sided polygon = (4 – 2) × 180°
= 2 × 180°
= 360°
| Also check: |
Exterior angle property
The sum of interior and the corresponding exterior angles at each vertex of any polygon are supplementary to each other. For a polygon;
|
Properties
The properties of polygons are based on their sides and angles.
- The sum of all the interior angles of an n-sided polygon is (n – 2) × 180°.
- The number of diagonals in a polygon with n sides = n(n – 3)/2
- The number of triangles formed by joining the diagonals from one corner of a polygon = n – 2
- The measure of each interior angle of n-sided regular polygon = [(n – 2) × 180°]/n
- The measure of each exterior angle of an n-sided regular polygon = 360°/n
Area and Perimeter Formulas
The area and perimeter of different polygons are based on the sides.
Area: Area is defined as the region covered by a polygon in a two-dimensional plane.
Perimeter: Perimeter of a polygon is the total distance covered by the sides of a polygon.
The formulas of area and perimeter for different polygons are given below:
| Name of polygon | Area | Perimeter |
| Triangle | ½ x (base) x (height) | a+b+c |
| Square | side2 | 4 (side) |
| Rectangle | Length x Breadth | 2(length+breadth) |
| Parallelogram | Base x Height | 2(Sum of pair of adjacent sides) |
| Trapezoid | Area = 1/2 (sum of parallel side)height | Sum of all sides |
| Rhombus | ½ (Product of diagonals) | 4 x side |
| Pentagon | \(\begin{array}{l}\frac{1}{4} \sqrt{5(5+2 \sqrt{5})} side^{2}\end{array} \) |
Sum of all five sides |
| Hexagon | 3√3/2 (side)2 | Sum of all six sides |
Let us see one of the frequently used and the primary types of polygon, i.e. triangle.
Triangles (3-gon)
A triangle is the simplest form of the polygon that has three sides and three vertices. The triangles are also classified into different types, based on the sides and angles.
An interesting fact about the Triangle:
|
Triangles – Based on Sides
- Equilateral triangle – Having all sides equal and angles of equal measure. It is also called an equiangular triangle.
- Isosceles triangle – Having any 2 sides equal and angles opposite to the equal sides are equal.
- Scalene triangle – Has all the 3 sides unequal.
See the below figure, to see the difference between the three types of triangles.

Triangles- Based on Angles
- Acute angled Triangle – Each angle is less than 90°
- Right Angled Triangle – Any one of the three angles equal to 90°
- Obtuse Angled Triangle – Any one angle is greater than 90°
The below figure shows the three types of angles, based on angles.

An Activity:
|
Quadrilaterals (4-gon)
A Quadrilateral is a polygon having a number of sides equal to four. That means a polygon is formed by enclosing four line segments such that they meet at each other at corners/vertices to make 4 angles.
Like triangles, a quadrilateral is also classified with different types:
The below figure shows the classification of quadrilaterals.

The table below gives the comparison of Opposite sides, angles, and diagonals of different Quadrilaterals.
| Quadrilateral | Opposite | Sides | All sides Equal | Opposite angles equal | Diagonal | Diagonal |
| Parallel | Equal | Equal | Perpendicular | |||
| Rectangle | ✔ | ✔ | ✖ | ✔ | ✔ | ✔ |
| Parallelogram | ✔ | ✔ | ✖ | ✔ | ✖ | ✖ |
| Rhombus | ✔ | ✔ | ✔ | ✔ | ✖ | ✔ |
| Trapezium | ✖
(Only one side) |
✖ | ✖ | ✖ | ✖ | ✖ |
| Square | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
Names of Polygon
| Polygon | No. of Sides | No. of Diagonal | No. of vertices | Interior Angle |
| Triangle | 3 | 0 | 3 | 60 |
| Quadrilateral | 4 | 2 | 4 | 90 |
| Pentagon | 5 | 5 | 5 | 108 |
| Hexagon | 6 | 9 | 6 | 120 |
| Heptagon | 7 | 14 | 7 | 128.571 |
| Octagon | 8 | 20 | 8 | 135 |
| Nonagon | 9 | 27 | 9 | 140 |
| Decagon | 10 | 35 | 10 | 144 |
| Hendecagon | 11 | 44 | 11 | 147.273 |
| Dodecagon | 12 | 54 | 12 | 150 |
| Triskaidecagon | 13 | 65 | 13 | 158.308 |
| Tetrakaidecagon | 14 | 77 | 14 | 154.286 |
| Pentadecagon | 15 | 90 | 15 | 156 |
Three Dimensional Shape (3-D shape)
A three-dimensional shape is a solid object that is formed by a combination of polygons and 2d shapes. Some of the 3d shapes which we can observe in real-life are:

- These are the shapes that can be projected on a piece of paper but cannot be drawn on paper. These shapes are known as solids.
| 2-D shape (Polygon) | 3-D Shape |
| Edge | Edge |
| Vertices | Vertices |
| — | Faces |
- 3-D shapes have faces as the distinguishing feature.

To know more about polygons, types of polygons and 3-D shapes, download BYJU’S – The Learning App.
Frequently Asked Questions – FAQs
What is a polygon?
What is called a polygon with 7 sides?
What is called a polygon with 9 sides?
How many diagonals does a polygon have?
What are the different types of polygons?
Regular polygon – all the sides and measure of interior angles are equal
Irregular polygon – all the sides and measure of interior angles are not equal, i.e. different
Convex polygon – all the interior angles of a polygon are strictly less than 180 degrees. The vertex will point outwards from the centre of the shape
Concave polygon – one or more interior angles of a polygon are more than 180 degrees. A concave polygon can have at least four sides. The vertex points towards the inside of the polygon.


This ia a great way of learning!!!!
Thank you for helping me
I like studing with buyjus its a very nice application
I am so happy for the conceptual understanding. It has helped me to help my students
This is helping to me for my studies
Its easy understand for teachers and parents. Great workbooks.
it is easy to understand and helps for math projects
easy to learn
Byjus app very good , it is easy to understantand and helps formath