A parallelogram is a two-dimensional geometrical shape whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of adjacent angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned about many 2D shapes and sizes such as circles, squares, rectangles, rhombus, etc. All of these shapes have a different set of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Let us learn here the definition, formulas and properties of a parallelogram.
| Table of contents: |
Parallelogram Definition
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. The Sum of all the interior angles equals 360 degrees.
A three-dimensional shape that has its faces in a parallelogram shape is called a parallelepiped. The area of the parallelogram depends on the base (one of its parallel sides) and its height (altitude drawn from top to bottom) of it. The perimeter of a parallelogram depends on the length of its four sides.
A square and a rectangle are two shapes which have similar properties to a parallelogram.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
If there is one parallel side and the other two sides are non-parallel, then it is a trapezium.
See the figure below:

In the figure above, you can see, ABCD is a parallelogram, where AB || CD and AD || BC.
Also, AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the same way, ∠B & ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠B + ∠C = 180
Facts:
|
Shape of Parellelogram
A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is not equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of a parallelogram should always be equal. Otherwise, it is not a parallelogram.
Special Parallelograms
Square and Rectangle: A square and a rectangle are two shapes which have similar properties to a parallelogram. Both have their opposite sides equal and parallel to each other. Diagonals of both shapes bisect each other.
Rhombus: If all the sides of a parallelogram are congruent or equal to each other, then it is a rhombus.
Rhomboid: A special case of a parallelogram that has its opposite sides parallel to each other, but adjacent sides are of unequal lengths. Also, the angles are non-right angles.
Trapezium: If there is one pair of side parallel and the other two sides are non-parallel, then it is a trapezium.
Angles of Parallelogram
A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, that means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.
Properties of Parallelogram
If a quadrilateral has a pair of parallel opposite sides, it’s a special polygon called Parallelogram. The properties of a parallelogram are as follows:
- The opposite sides are parallel and equal
- The opposite angles are equal
- The consecutive or adjacent angles are supplementary
- If any one of the angles is a right angle, then all the other angles will be at right angle
- The two diagonals bisect each other
- Each diagonal bisects the parallelogram into two congruent triangles
- The Sum of the square of all the sides of a parallelogram is equal to the sum of the square of its diagonals. It is also called parallelogram law
Also, read:
Formulas (Area & Perimeter)
The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve problems based on them.
Area of Parallelogram
Area of a parallelogram is the region occupied by it in a two-dimensional plane. Below is the formula to find the parallelogram area:
Area = Base × Height

In the above figure, ||gramABCD, Area is given by;
| Area = a b sin A = b a sin B |
where a is the slant length of the side of ||gramABCD and b is the base.
Check here: Area of a Parallelogram Formula
Perimeter of Parallelogram
The perimeter of any shape is the total distance covered around the shape or the total length of any shape. Similarly, the perimeter of a parallelogram is the total distance of the boundaries of the parallelogram. To calculate the perimeter value, we have to know the values of its length and breadth. The parallelogram has its opposite sides equal in length. Therefore, the formula to calculate the perimeter is written as;
| Perimeter = 2 (a+b) units |
Where a and b are the length of the sides of the parallelogram.
Types of Parallelogram
There are mainly four types of parallelograms, depending on various factors. The factors which distinguish between all of these different types of parallelogram are angles, sides etc.
- In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, then it’s a rhombus. All the properties are the same for rhombus as for parallelogram.
- Other two special types of a parallelogram are:
- Rectangle
- Square
Is Square a Parallelogram?
Yes, a square is considered as a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.
Is Rectangle a Parallelogram?
Yes, a rectangle is also a parallelogram, because it satisfies the conditions or meets the properties of parallelogram such as the opposite sides are parallel and diagonals bisect each other.
Parallelogram Theorems
Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF, on the same base DC and between the same parallel line AB and FC.
To prove that area (ABCD) = area (ABEF).

Proof:
Consider the above figure –
In ∆ADF and ∆BCE,
AD = BC (Since, ABCD is a parallelogram ∴ AD=BC)
AF = BE (Since, ABEF is a parallelogram ∴AF=BE)
∠ADF = ∠BCE (Corresponding Angles)
∠AFD = ∠BEC (Corresponding Angles)
∠DAF = ∠CBE (Angle Sum Property)
Therefore, ∆ADE ≅ ∆BCF (From SAS-rule)
Area(ADF) = Area(BCE) (By congruence area axiom)
Area(ABCD) = Area(ABED) + Area(BCE)
Area(ABCD) = Area(ABED)+Area(ADF)
Area(ABCD) = Area(ABEF)
Hence, the area of parallelograms on the same base and between the same parallel sides is equal.
Corollary
A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Proof: Since a rectangle is also a parallelogram so, the result is a direct consequence of the above theorem.
Theorem: The area of a parallelogram is the product of its base and the corresponding altitude.
Given: In a parallelogram ABCD, AB is the base.
To prove that Area(||gmABCD) = AB×AL
Construction: Complete the rectangle ALMB by Drawing BM perpendicular to CD.

Consider the figure given below:
Parallelogram ABCD and rectangle ABML are on the same base and between the same parallels AB and LC.
area of parallelogram ABCD = area of parallelogram ABML
We know that area of a rectangle = length x breadth.
Therefore, area of parallelogram ABCD = AB x AL
Hence, the area of a parallelogram is the product of any base of it and the corresponding altitude.
Difference Between Parallelogram and Rhombus
| Parallelogram | Rhombus |
| A quadrilateral that has its opposite sides equal and parallel | A quadrilateral that has all its sides congruent |
| Diagonals bisect each other | Diagonals bisect each other at 90 degrees |
| Opposite angles are of equal measure | Opposite angles are of equal measure |
Examples on Parallelogram
| Example 1:
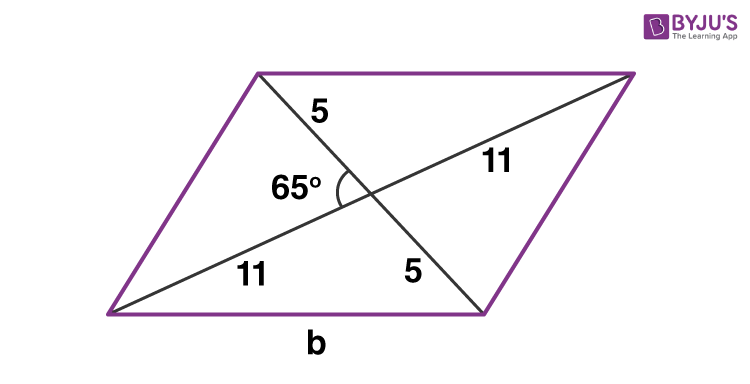
Find the area of a parallelogram whose base is 5 cm and height is 8 cm. Solution-: Given, Base = 5 cm and Height = 8 cm. We know, Area = Base x Height Area = 5 × 8 Area = 40 Sq.cm Example 2: Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees. Solution: We know that the diagonals of a parallelogram bisect each other. Hence, half the diagonal length will be 5 and 11 cm.
The angle opposite to the side b comes out to be 180 – 65 = 115° We use the law of cosines to calculate the base of the parallelogram – b² = 5² + 11² – 2(11)(5)cos(115°) b² = 25 + 121 – 110(-0.422) b² = 192.48 b = 13.87 cm.
After finding the base, we need to calculate the height of the given parallelogram. To find the height, we have to calculate the value of θ, so we use the sine law 5/sin(θ) = b/sin(115)
Now we extend the base and draw in the height of the figure and denote it as ‘h’. The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h. So sin θ = h/22 h = 7.184 cm Area = base × height A = 13.87 × 7.184 A = 99.645 sq.cm |
Hope this discussion has cleared all your doubts regarding parallelograms and their properties. Register with BYJU’S to learn more about quadrilaterals and other Maths concepts.
Video Lesson

Frequently Asked Questions (FAQs) on Parallelogram
What is a parallelogram?
What are the examples of a parallelogram?
Square
Rectangle
Rhombus
A kit and a trapezium cannot be considered as a parallelogram, as they don’t have two pairs of parallel sides.
What are the area and perimeter of a parallelogram?
Area = Base x Height (in square unit)
The area of a parallelogram without height is given by:
Area = ab sin x
Where a and b are the two adjacent sides of a parallelogram and x is the angle between them.
Perimeter is the total length of boundaries of a parallelogram. It is equal to the sum of all four sides.
Perimeter = 2(a+b)
What is the shape of a parallelogram?
What are the four important properties of a parallelogram?
Opposite angles are congruent
Consecutive angles are supplementary
Diagonals bisect each other




Ssc maths how to problems solve in easy way
Please visit: https://byjus.com/maths/preparation-tips-for-class-10-maths-exam/
The best website or a learning field to encourage students to do more.
Really well done.
Very Helpful
Thanks for the detailed information it’s very easy to understand especially with the diagrams and examples.