Perimeter of a Parallelogram

The perimeter of a parallelogram is the total distance enclosed by its boundary. Since the parallelogram is a type of quadrilateral, thus it has four sides. The perimeter of the parallelogram will be equal to the sum of all these four sides. Geometry is a branch of mathematics that deals with the study of different geometrical shapes. It is of two types:

• Two-dimensional Geometry
• Three-dimensional Geometry

A parallelogram is a two-dimensional geometric shape bounded by four sides. The properties of a parallelogram are:

• The pair of opposite sides of a parallelogram are parallel and equal to each other.
• Opposite angles are equal in measure
• Diagonals of parallelogram bisect each other
• Pair of adjacent angles are supplementary
• Sum of all interior angles is equal to 360 degrees

Now, let us find here the perimeter of parallelogram along with formulas and also see some solved examples to understand better.

What is the Perimeter of a Parallelogram?

The perimeter of a parallelogram is defined as the total length of the boundaries, surrounding it. The sum of all the sides of a parallelogram is known as the perimeter of a parallelogram.

The parallelogram perimeter is similar to the perimeter of the rectangle. Since, both the shapes having similar properties, the area and the perimeter of the parallelogram have more or less the same formulae. By adding all the boundaries or sides of the parallelogram, we can easily find the parallelogram perimeter.

Perimeter of a Parallelogram Formula

Let “a” and “b” be the sides of a parallelogram. Therefore, the perimeter of a parallelogram formula is as follows:

We know that the opposite sides of a parallelogram are parallel and equal to each other. Thus, the formula for finding the perimeter of a parallelogram is given by:

So, the perimeter of Parallelogram, P = a + b + a + b units

P = 2a +2b

P = 2(a+b)

Therefore, the perimeter of a parallelogram, P = 2(a+b) units

How to Find Perimeter of Parallelogram?

We have already discussed the formula to calculate the perimeter of a parallelogram, given the length of its parallel sides. Thus, combining it there are three cases to find the perimeter of a parallelogram, when:

• Length of adjacent sides are given
• Length of base and height along with one interior angle is given

Let us find the perimeter of a parallelogram based on the above three cases.

Perimeter of a Parallelogram Given Two Adjacent Sides

This is the common scenario, when we have the length of two adjacent sides of a parallelogram given to us. Thus, we can simply the formula:

Perimeter of a parallelogram = 2 (a + b)

where a and b are the length of two adjacent sides of parallelogram

Example: If a = 10 cm and b = 5 cm, then the perimeter of a parallelogram;

P = 2(a + b) = 2(10 + 5) = 2 (15) = 30 cm

Perimeter of a parallelogram with Base, Height and an Angle

The perimeter of the parallelogram with base and height is given using the property of the parallelogram. If “b” is the base of the parallelogram and “h” is the height of the parallelogram, then the formula is given as follows:

According to the property of the parallelogram, the opposite sides are parallel to each other, and the parallelogram perimeter is defined as two times of the base and height.

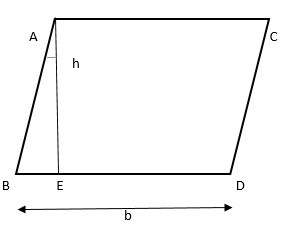
Thus, the formula for the perimeter of a parallelogram is:

P = 2 (b +h/cos θ)

where θ is the angle BAE, formed between the height and side of the parallelogram, i.e. AE and AB.

Area and Perimeter of a Parallelogram

We know that the area of a parallelogram is equal to the product of base and height.

A = b x h square units ……(1)

The relationship between the area and perimeter of a parallelogram is:

P = 2 (a+b) units

Therefore, the value of b in terms of P is

P/2 = a + b

b=(P/2) – a

Now, substitute the value of b in (1)

A = ((P/2) – a)h Square units

Related Articles

• Parallelogram
• Perimeter of a Parallelogram
• Angles of a Parallelogram
• Area of Parallelogram
• Perimeter of Rectangle
• Perimeter of Square
• Perimeter of Triangle

Solved Examples on Perimeter of a Parallelogram

Example 1:

Find the perimeter of a parallelogram whose base and side lengths are 10cm and 5cm, respectively.

Solution:

Given:

Base length of a parallelogram = 10 cm

Side length of a parallelogram = 5 cm

We know that the perimeter of a parallelogram, P = 2(a+b) units.

Substitute the values

P = 2(10+5)

P = 2(15)

P = 30 cm

Therefore, the perimeter of a parallelogram is 30 cm.

Example 2:

Find the length of another side of the parallelogram whose base is 5 cm and the perimeter is 40 cm.

Solution:

Given:

Base, h = 5cm

Perimeter, p = 40cm

We know, that the perimeter of a parallelogram is,

p=2 (a+b) units

Now substitute the given values in the formula,

40 = 2 (a +5)

40 = 2a + 10

2a = 40-10

2a = 30

a = 30/2

a = 15 cm

Thus, the length of other side of the parallelogram is 15 cm.

Practice Questions

1. Find the perimeter of a parallelogram whose two adjacent sides are:
   1. 3cm , 5cm
   2. 6cm, 10cm
   3. 10cm, 15cm
   4. 50mm, 100mm
2. What is the perimeter of a parallelogram whose one of its sides is 15 m, height is 20 m, and one of its interior angles is 30 degrees.