Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value. For example, 2/4 and 3/6 are equivalent fractions, because they both are equal to the ½. A fraction is a part of a whole. Equivalent fractions represent the same portion of the whole.
For each fraction, we can find its equivalent fraction by multiplying both numerator and denominator with the same number. For example, we have to find the third equivalent fraction of ⅔; then we have to multiply 2/3 by 3/3. Hence, 2/3 × (3/3) = 6/9, is the fraction equivalent to 2/3.
| Table of contents: |
What are Equivalent Fractions?
Equivalent fractions state that two or more than two fractions are said to be equal if both results the same fraction after simplification. Let us say, a/b and c/d are two fractions, after the simplification of these fractions, both result in equivalent fractions, say e/f, then they are equal to each other.
For example, the equivalent fraction of 1/3 is 5/15, because if we simplify 5/15, then the resulted fraction is the same.
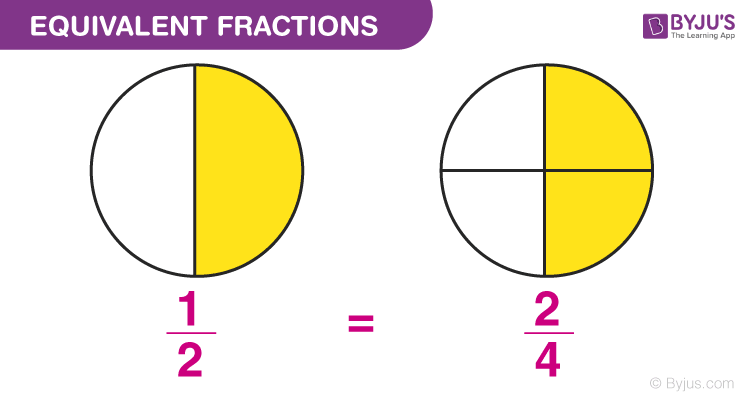
The biggest question here can be, why do they have equal values in spite of having different numbers?
The answer to this question is that, as the numerator and denominator are not co-prime numbers, therefore they have a common multiple, which on division gives exactly the same value.
Example of Equivalent Fraction
Take for an example:
1/2 = 2/4 = 4/8
But, it is clearly seen that the above fractions have different numerators and denominators.
Dividing both numerator and denominator by their common factor, we have:
In the same way, if we simplify 2/4, again get 1/2.
Equivalent fractions of a mixed fraction:
Let us consider a mixed fraction to find its equivalent fraction.
Mixed fraction = 1 ½
Now, convert this fraction into an improper fraction.
1 ½ = (1 × 2 + 1)/2 = (2 + 1)/2 = 3/2
The equivalent fractions for the above fraction are:
3/2 = (3 × 2)/(2 × 2) = 6/4
3/2 = (3 × 3)/(2 × 3) = 9/6
3/2 = (3 × 4)/(2 × 4) = 12/8 and so on.
How to Find Equivalent Fractions?
Equivalent fractions are evaluated by multiplying or dividing both the numerator and the denominator by the same number. Therefore, equivalent fractions, when reduced to their simplified value, will all be the same.
Multiplying numerator and denominator by the same number
For example, consider the fraction 1/5
- Multiplying numerator and denominator with 2, we get 1/5 × 2/2 = 2/10
- Multiplying numerator and denominator with 3, we get 1/5 × 3/3 = 3/15
- Multiplying numerator and denominator with 4, we get 1/5 × 4/4 = 4/20
Therefore, we can conclude that,
1/5 = 2/10 = 3/15 = 4/20
Dividing numerator and denominator by the same number
For example, we need to find the equivalent fraction of 18/32.
Find the Highest common factor of 18 and 32.
HCF (18, 32) = 2
Now divide the numerator and denominator by 2, to get the equivalent fraction of 18/32.
(18÷2)/(32÷2) = 9/16
Hence, 9/16 is equivalent to 18/32.
Note: We can only multiply or divide by the same numbers to get an equivalent fraction and not addition or subtraction. Simplification to get equivalent numbers can be done to a point where both the numerator and denominator should still be whole numbers.
Equivalent Fractions Chart
Let us see the equivalent fractions for unit fractions.
| Unit Fraction | Equivalent Fractions |
| 1/2 | 2/4, 3/6, 4/8.. |
| 1/3 | 2/6, 3/9, 4/12.. |
| 1/4 | 2/8, 3/12, 4/16.. |
| 1/5 | 2/10, 3/15, 4/20,.. |
| 1/6 | 2/12, 3/18, 4/24,.. |
| 1/7 | 2/14, 3/21, 4/28,.. |
| 1/8 | 2/16, 3/24, 4/32,.. |
| 1/9 | 2/18, 3/27, 4/36,.. |
Methods to Determine Equivalent Fractions
How can we determine if two fractions are equivalent or not? It is possible by these methods:
- Method 1: Make the Denominators the same
- Method 2: Cross Multiply
- Method 3: Convert to decimals
Method 1:
By making the denominators the same, we can evaluate if two fractions are equivalent.
For example, find if 2/3 and 6/9 are equivalent.
LCM of 3 and 9 = 9
Multiply 2/3 by 3/3 to make the denominator equal to 9.
2/3 × 3/3 = 6/9
Hence, by making the denominators the same, we can see, 2/3 and 6/9 are equivalent fractions.
Method 2:
Given, two fractions 1/2 and 3/6
Cross multiply both the fractions to get:

1 x 6 = 6
2 x 3 = 6
Since, both the values are equal, therefore, 1/2 and 3/6 are equivalent fractions.
Method 3:
If two fractions are given, we can simply find their decimals to check if they are equivalent fractions.
Let us check if 1/4 and 3/12 are equivalent fractions by converting them in decimal form.
1/4 = 0.25
3/12 = 0.25
Since, both the fractions result in the same decimal, thus they are equivalent.
Solved Examples
Example 1: The given fractions 5/16 and x/12 are equivalent fractions, then find the value of x.
Solution:
Given: 5/16 = x/12
x = (5 × 12)/16
x = 60/16
x =15/4
Therefore, the value of x is 15/4.
Example 2: Two fractions 3/5 and 4/x are equivalent. Find the value of x.
Solution: Given,
3/5 = 4/x
x = (4 × 5)/3
x = 20/3
Example 3: What fractions are the same as ¼?
Solution: To find equivalent fractions of ¼ we need to multiply the numerator and denominator by the same numbers. Hence,
¼ × (2/2) = 2/8
¼ × (3/3) = 3/12
¼ × (4/4) = 4/16
¼ × (5/5) = 5/20
And so on.
Video Lesson on Fractions

Have persisting doubts on any topic? Try reaching out to our mentors only with BYJU’S – The Learning App.
Practice Questions
- Find the equivalent fraction of 8/10
- What is the simplest form of 9/81?
- Write the fraction three-sevenths as an equivalent fraction with a denominator of 21.
- Write the fraction five-eighth as an equivalent fraction with a denominator of 24.
Related Articles
Frequently Asked Questions on Equivalent Fractions
What are equivalent fractions?
What are the examples of equivalent fractions?
2/4 and 3/6
⅓ and 3/9
⅕ and 5/25
¾ and 12/16
How to determine whether fractions are equivalent?
But, ⅚ and 10/12 are equivalent fractions because 10/12 = ⅚.
What is the equivalent fraction of ⅗?
⅗ × (2/2) = 6/10
What are the equivalent fractions of 5/10?
½, 2/4, 3/6, 4/8 and so on.


Amazing apps study
Hi, yes please. Can you do it for 8/9?
The equivalent fraction to 8/9 is 16/18
how did you find it please teach me?
Multiply numerator and denominator by a common factor, to get the equivalent fractions.
(8/9) x (2/2)
(8×2)/(9×2)
16/18
what is equal to 1/5?
2/10 is equivalent to 1/5
What is equivalent to 7/12 because I’m in fifth grade
Multiply the fraction 7/12 by any natural number both in numerator and denominator to get its equivalent.
For example, (7/12) * (3/3) = 21/36
what is equivalent to 1/10
2/20,3/30, etc.
What is equivalent to 4/5
Multiply 4/5 with 2/2 to get: 8/10.
Thus, 8/10 is equivalent to 4/5