Tangent to a Circle

A line that touches the circle at a single point is known as a tangent to a circle. The point where tangent meets the circle is called point of tangency. The tangent is perpendicular to the radius of the circle, with which it intersects. Tangent can be considered for any curved shapes. Since tangent is a line, hence it also has its equation. In this article, we will discuss the general equation of a tangent in slope form and also will solve an example to understand the concept.

Table of Contents:

• Definition
• Equation
• Condition of Tangency
• Properties
• Formula
• Theorems
• Example

Definition

Tangent to a circle is the line that touches the circle at only one point. There can be only one tangent at a point to circle. Point of tangency is the point at which tangent meets the circle. Now, let’s prove tangent and radius of the circle are perpendicular to each other at the point of contact.

Consider a circle in the above figure whose centre is O. AB is the tangent to a circle through point C.
Take a point D on tangent AB other than C and join OD. Point D should lie outside the circle because; if point D lies inside, then AB will be a secant to the circle and it will not be a tangent.

Therefore, OD will be greater than the radius of circle OC. This happens for every point on AB except the point of contact C.
It can be concluded that OC is the shortest distance between the centre of circle O and tangent AB.
Since, the shortest distance between a point and a line is the perpendicular distance between them,
OC is perpendicular to AB.

From the above discussion, it can be concluded that:

• The tangent touches the circle at only one point
• We can call the line containing the radius through the point of contact as ‘normal’ to the circle at the point

Note: The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide.

Also, read:

• Circles
• Tangent
• Equation of Tangent and Normal

General Equation

Here, the list of the tangent to the circle equation is given below:

• • The tangent to a circle equation x²+ y²=a² at (x₁, y₁) is xx₁+yy₁= a²
  • The tangent to a circle equation x²+ y²+2gx+2fy+c =0 at (x₁, y₁) is xx₁+yy₁+g(x+x₁)+f(y +y₁)+c =0
  • The tangent to a circle equation x²+ y²=a² at (a cos θ, a sin θ ) is x cos θ+y sin θ= a
  • The tangent to a circle equation x²+ y²=a²  for a line y = mx +c is y = mx ± a √[1+ m²]

Condition of Tangency

The tangent is considered only when it touches a curve at a single point or else it is said to be simply a line. Thus, based on the point of tangency and where it lies with respect to the circle, we can define the conditions for tangent as:

• When point lies inside the circle
• When point lies on the circle
• When point lies outside the circle

When the Point Lies Inside the Circle

Consider the point P inside the circle in the above figure; all the lines through P is intersecting the circle at two points.
It can be concluded that no tangent can be drawn to a circle which passes through a point lying inside the circle.

When the Point Lies on the Circle

From the figure; it can be concluded that there is only one tangent to a circle through a point which lies on the circle.

When the Point Lies Outside the Circle

From the above figure, we can say that
There are exactly two tangents to circle from a point which lies outside the circle.

Tangent Properties

• The tangent always touches the circle at a single point.
• It is perpendicular to the radius of the circle at the point of tangency
• It never intersects the circle at two points.
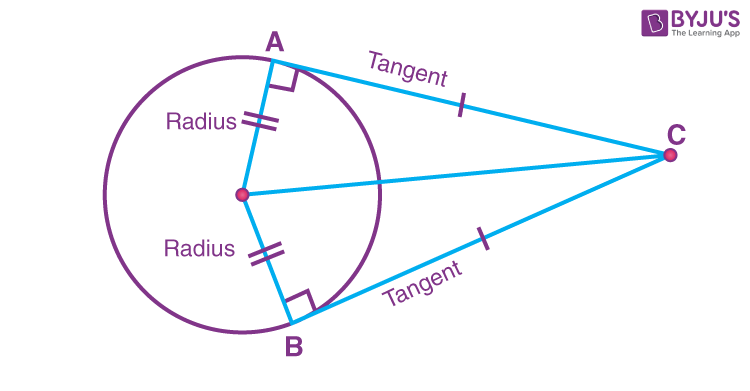
• The length of tangents from an external point to a circle are equal.

Tangent Formula

Suppose a point P lies outside the circle. From that point P, we can draw two tangents to the circle meeting at point A and B. Now let a secant is drawn from P to intersect the circle at Q and R. PS is the tangent line from point P to S. Now, the formula for tangent and secant of the circle could be given as:

PR/PS = PS/PQ

PS²=PQ.PR

Tangent Theorems

Theorem 1: The tangent to the circle is perpendicular to the radius of the circle at the point of contact.

Theorem 2: If two tangents are drawn from an external point of the circle, then they are of equal lengths

Video Lessons on Circles

Solved Example

Example: AB is a tangent to a circle with centre O at point A  of radius 6 cm. It meets the line OB such that OB = 10 cm. What is the length of AB?

We know that AB is tangent to the circle at A.
Since tangent AB is perpendicular to the radius OA,
ΔOAB is a right-angled triangle and OB is the hypotenuse of ΔOAB.
By using Pythagoras theorem,

To know more about properties of a tangent to a circle, download BYJU’S – The Learning App from Google Play Store.