Vertices, Faces and Edges are the three properties that define any three-dimensional solid. A vertex is the corner of the shape whereas a face is a flat surface and an edge is a straight line between two faces. 3d shapes faces, edges and vertices, differs from each other.
In our day-to-day life activities, we come across a number of objects of different shapes and sizes. There are golf balls, doormats, ice-cream cones, coke cans and so on. These objects have different characteristic properties such as length, breadth, diameter, etc., which set them apart from one another. But no matter how different their dimensions are, all of them occupy space and have three dimensions. So they are referred to as three-dimensional Shapes or solids.
There are figures that can be represented on a plane (as a piece of paper) and have 2 dimensions, length, and breadth. And they are referred to as two-dimensional or plane figures. In this article, we will discuss the faces, edges and vertex meaning in Maths for the solid objects.
| Table of contents: |
What are Vertices?
The formal definition for the vertex meaning in Maths is defined as a point where two or more edges meet. Vertices are the corner points.
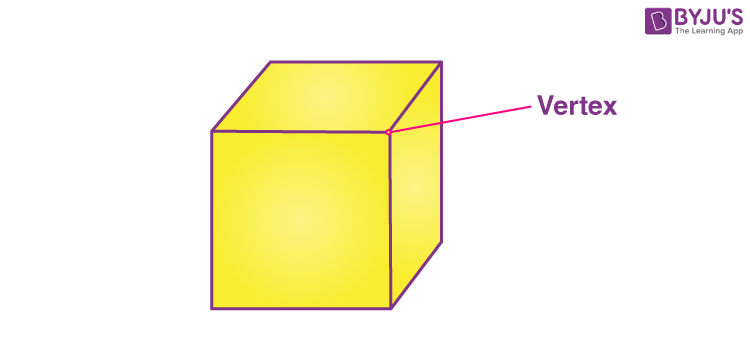
- Cubes and cuboids have 8 vertices.
- Cones have 1 vertex.
- Cylinders have no vertex.
- Spheres have no vertex (the surface is a curve).
What are Faces?
Every individual flat surface of a solid is called its face. Solids have more than one face.
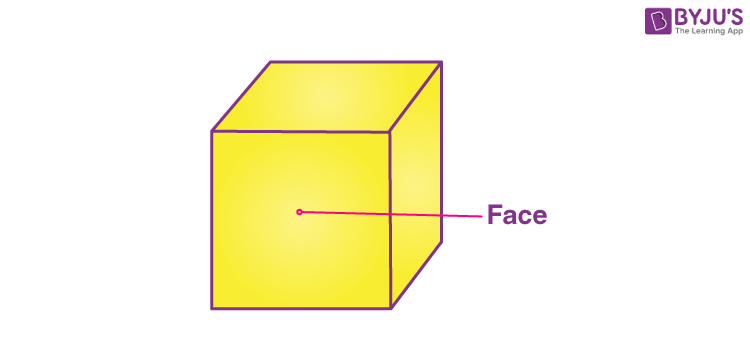
- Cubes and cuboids have 6 faces.
- Cones have a flat face and a curved face.
- Cylinders have 2 flat faces and a curved face.
- A sphere has a curved face.
What are Edges?
The line segment which acts as an interface between two faces is called an edge. Sometimes it is also described as the line segment joining two vertices.
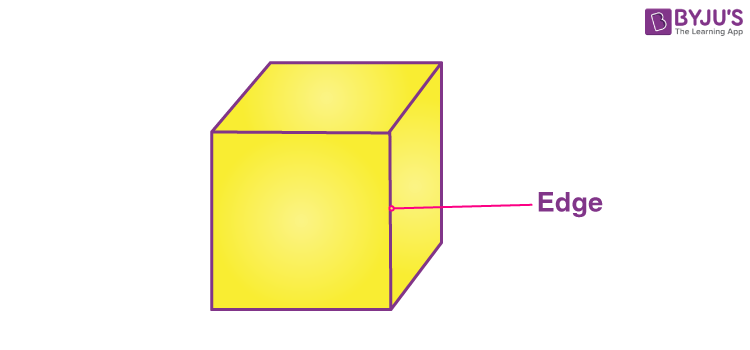
- Cubes and cuboids have 12 edges.
- Cones have 1 edge.
- Cylinders have 2 edges.
- Sphere has no edge.
Sides of Shapes
The word “side” is usually used for polygons such as a square has four sides, a triangle has three sides, a pentagon has five sides.
Vertices, Faces and Edges of 3D shapes
Let us compare the vertices, faces and edges of solid shapes with the help of a table.
| Solid Name | Vertices | Faces | Edges |
| Cube | 8 | 6 (square faces) | 12 |
| Cuboid | 8 | 6 (rectangular faces) | 12 |
| Cone | 1 | 2 | 1 |
| Cylinder | 0 | 3 | 2 |
| Sphere | 0 | 1 | 0 |
Relation Between Vertices, Faces and Edges (Euler’s Formula)
The relation between vertices, faces and edges can be easily determined with the help of Euler’s Formula. Having learned about the faces, edges, and vertices of solids, let us note an interesting relationship between the three of them. It is to be kept in mind that the formula holds good for closed solids which have flat faces and straight edges such as the cuboids. It cannot be used for cylinders because they have curved edges.
Euler’s formula is given by
F + V – E = 2
Where F, V, and E are the number of faces, vertices, and edges of the polyhedra respectively.
Related Articles
Solved Examples
Q.1: A cube has 6 faces, 12 edges and 8 vertices. Prove Euler’s formula for the cube.
Solution: Given, a cube has 6 faces, 12 edges and 8 vertices.
Therefore, according to Euler’s formula,
F + V – E = 2
Taking L.H.S.,
6 + 8 – 12
= 14 – 12
= 2 (R.H.S)
Hence, proved.
Q.2: How many faces, edges and vertices are there for a triangular prism?
Solution: A triangular prism is a polyhedron that has 5 faces, 6 vertices and 9 edges.
Practice Questions
- What is the meaning of vertices?
- How many vertices are there for a cone?
- Tell the number of edges for a sphere.
- A cylinder has 5 surfaces. True or false.
To learn more about edges, faces, and vertices meaning, formulas for different solid shapes in Maths, download BYJU’S – The Learning App.


Comments