A 3D shape or an object is made up of a combination of certain parts. Most of the solid figures consist of polygonal regions. These regions are- faces, edges, and vertices. Solid geometric shapes which have faces, edges and vertices are known as polyhedrons.
Faces of 3D Shapes
- The flat surface of a polyhedron is its face. Solid shapes can have more than one face. The cube shown below has 6 faces viz. ABCD, EFGH, ADHE, DHGC, BFGC, and AEFB.
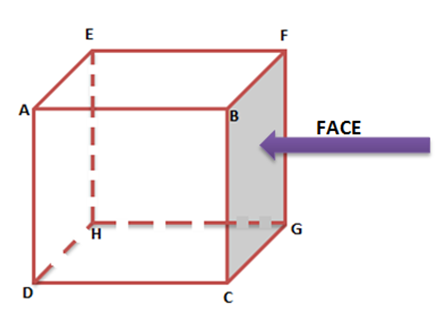
- Cubes and cuboids have 6 faces.
- Cones have a flat face and a curved face.
- Cylinders have 2 flat faces and a curved face.
- A sphere has a curved face.
Edges of 3D Shapes
- The faces meet each other at edges. Edges are straight lines which serve as the junction of two faces. The cube shown below has 12 edges namely AB, BF, EF, AE, AD, DH, EH, HG, FG, BC, CG, and CD.
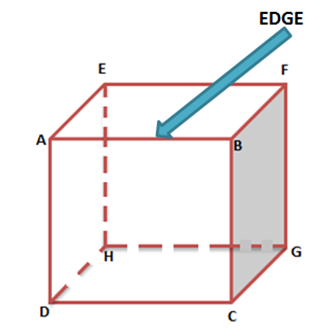
- Cubes and cuboids have 12 edges.
- Cones have 1 edge.
- Cylinders have 2 edges.
- A sphere has no edge.
Vertices of 3D Shapes
- The points of intersection of edges denote the vertices. Vertices are represented by points. In the cube shown below A, B, C, D, E, F, G, and H are the 8 vertices of the cube.
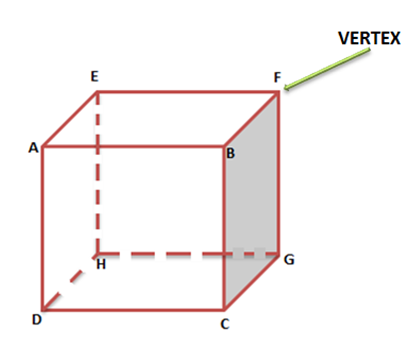
- Cubes and cuboids have 8 vertices.
- Cones have 1 vertex.
- Cylinders have no vertex.
- Spheres have no vertex (the surface is a curve).
Now that, we are familiar with polyhedrons let’s move onto to their types.
Types of Polyhedron
- Convex Polyhedron: If the surface of a polyhedron (which consists of its faces, edges, and vertices) does not intersect itself and the line segment connecting any two points of the polyhedron lies within its interior part or surface then such a polyhedron is a convex polyhedron.
- Concave Polyhedron: A non-convex polyhedron is termed as a concave polyhedron.

Euler’s Formula :
According to Euler’s formula for any convex polyhedron, the number of Faces (F) and vertices (V) added together is exactly two more than the number of edges (E).
F + V = 2 + E
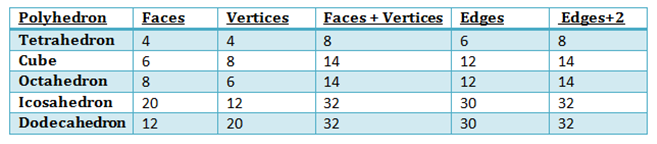
A polyhedron is known as a regular polyhedron if all its faces constitute regular polygons and at each vertex the same number of faces intersect.
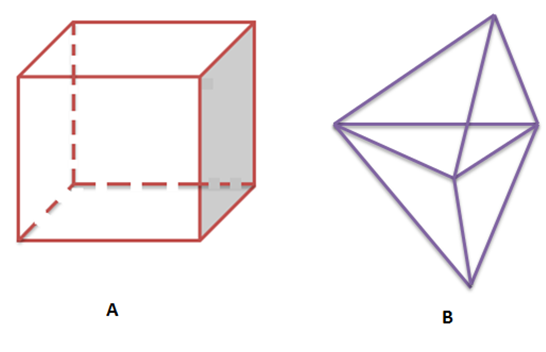
Fig A is a regular polyhedron as all the faces are regular polygons and B is an irregular polygon.
To know more about two dimensional and three-dimensional shapes, visit our site BYJU’S.



Comments