We come across a number of objects of different shapes and sizes in our day-to-day life such as golf balls, doormats, ice-cream cones, coke cans, etc. These objects have different characteristic properties such as length, breadth, diameter, which set them apart from one another. All these three-dimensional shapes occupies space, as per their configurations. They are referred to as three-dimensional or solid shapes. In this article, we will discuss views of different sections of solids.
Viewing Different Sections of Solids
A 3D object can be viewed in different ways. Two of them are:
- Cutting or Slicing
- Shadow Play
Cutting or Slicing
Before we go ahead with slicing a 3D object for viewing different sections of solids, let us know about the term ‘cross-section’. A cross-section is the exposed surface of a solid that you get when you make a cut through it. Thus, it does not contain any piece of the original face. It all comes from “inside” the object.
One way to view a 3D object is by cutting or slicing it to obtain its cross-section. So let us take an example of a cheese block. The cheese block is like a cuboid with a square face. Now if you slice or cut it with a knife vertically, a square cross-section is obtained. And when you slice it horizontally, a rectangular cross-section is obtained. Similarly, you can slice along different axes to get different cross-sections of solids.
Shadow Play
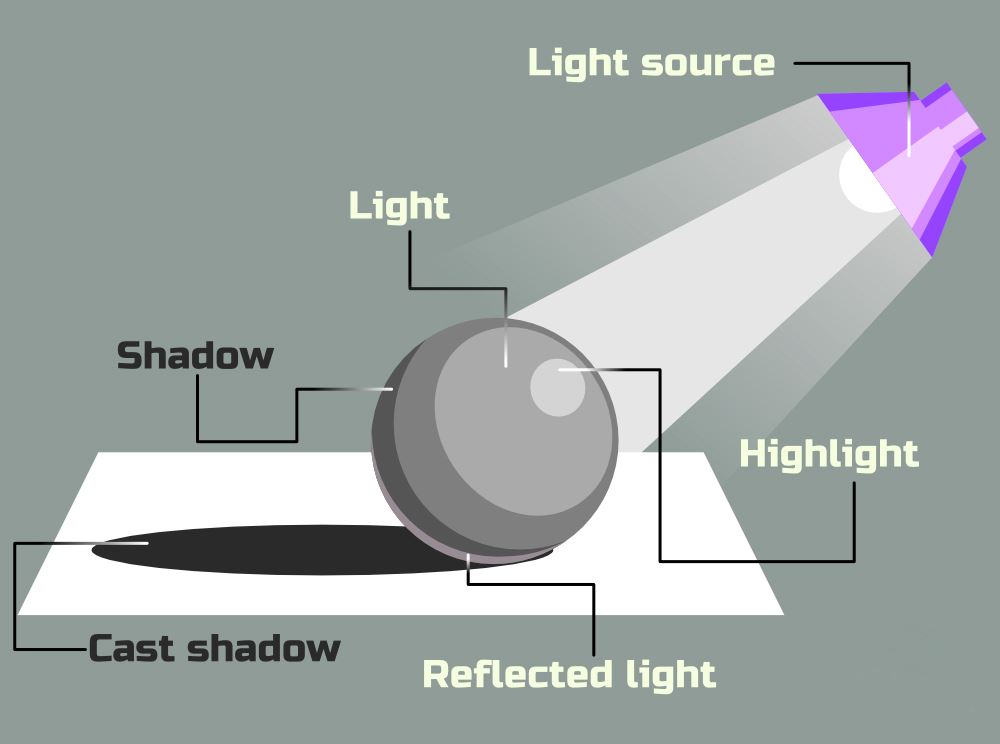
Shadows are another way to view sections of solids in two dimensions. Let us demonstrate it through activity. You will require a source of light (e.g., a torch), a few solids (cuboid, cone, sphere, etc.) and a screen for the activity. The steps are:
- Place a solid in front of the screen.
- Bring the torch in front of the solid from the side opposite to the screen.
- View the shadow of the solid on the screen.

Comments