In geometry, a semicircle is a plane figure that is formed by dividing a circle into exactly two parts. So, we can write the formulas of area and perimeter for a semicircle using the area and perimeter of a circle. In this article, you will learn how to identify a semicircle and find the area and perimeter of a semicircle with the help of formulas and solved examples.
| Table of Contents: |
What is a Semi-Circle?
A semicircle is formed when a lining passing through the centre touches the two ends on the circle. Thus, by joining two semicircles we get a circular shape.
Semi Circle Shape
When a circle is cut into two halves or when the circumference of a circle is divided by 2, we get a semicircular shape.
Since a semicircle is half that of a circle, hence the area will be half that of a circle.
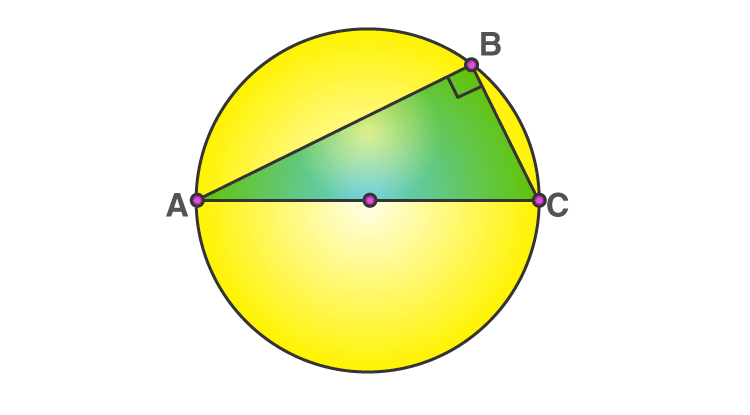
In the below figure, the line AC is called the diameter of the circle. The diameter divides the circle into two halves such that they are equal in area. These two halves are referred to as the semicircles.
A circle is a locus of points equidistant from a given point which is the centre of the circle. The common distance from the centre of a circle to its point is called a radius.
Thus, the circle is entirely defined by its centre (O) and radius (r).
Area of Semi-Circle
The area of a semicircle is half of the area of the circle. As the area of a circle is πr2. So, the area of a semicircle is 1/2(πr2 ), where r is the radius. The value of π is 3.14 or 22/7.
| Area of Semicircle = 1/2 (π r2) |
Derivation
As defined above, the area of a semicircle is half of the area of a circle. Also, we can say that the area of a circle is the number of square units inside that circle.

Let us generate the above figure. This polygon can be broken into n isosceles triangle (equal sides being radius).
Thus, one such isosceles triangle can be represented as shown below.

The area of this triangle is given as ½(h*s)
Now for n number of polygons, the area of a polygon is given as
½(n*h*s)
The term n × s is equal to the perimeter of the polygon. As the polygon gets to look more and more like a circle, the value approaches the circle circumference, which is 2 × π × r. So, substituting 2×π×r for n × s.
Polygon area = h/2(2 × π × r)
Also, as the number of sides increases, the triangle gets narrower and so when s approaches zero, h and r have the same length. So substituting r for h:
Polygon area = h/2(2 × π × r)
= (2 × r × r × π)/2
Rearranging this we get
Area = πr2
Now the area of a semicircle is equal to half of that of a full circle.
Therefore,
Area of a semicircle = (πr2)/2
Perimeter of Semicircle
The perimeter of a semicircle is the sum of half of the circumference of the circle and its diameter. As the perimeter of a circle is 2πr or πd. So, the perimeter of a semicircle is 1/2 (πd) + d or πr + 2r, where r is the radius.
Therefore,
| The perimeter of Semicircle = (1/2) π d + d
Or Circumference = (πr + 2r) |
Semi circle Formula
The below table shows the formulas associated with the semicircle of radius r.
| Area | (πr2)/2 |
| Perimeter (Circumference) | (½)πd + d; when diameter (d) is known |
| πr + 2r | |
| Angle in a semicircle | 90 degrees, i.e. right angle |
| Central angle | 180 degrees |
Video Lessons on Circles
Introduction to Circles

Parts of a Circle

Area of a Circle

All about Circles

Semi circle Examples
Example 1:
Find the area of a semicircle of radius 28 cm.
Solution:
Given,
Radius of semi circle = r = 28 cm
Area of semi circle = (πr2)/2
= (½) × (22/7) × 28 × 28
= 1232
Therefore, the area of the semi-circle is 1232 sq. cm.
Example 2:
What is the perimeter of a semicircle with a diameter of 7 cm?
Solution:
Given,
Diameter of semicircle = d = 7 cm
Formula for the circumference (perimeter) of a semicircle using its diameter = (½)πd + d
Substitute the value of d, we get;
= (½) × (22/7) × 7 + 7
= 11 + 7
= 18
Therefore, the perimeter of the semicircle is 18 cm.
Practice Problems
- Find the circumference and area of a semicircle whose diameter is 21 cm.
- If the perimeter of a semicircle is 36 units, then find the radius.
- Is the perimeter of a semicircle half the perimeter of a circle? Justify your answer.
Frequently Asked Questions on Semicircle
Is a semicircle half the circle?
What shape is a semicircle?
What is the semicircle angle?
What is the area of a semicircle?
Area of semicircle = (1/2) × Area of circle = (1/2)πr^2
What is the perimeter formula of a semicircle?
Semicircle circumference = (1/2)2πr + 2π = πr + 2r



The app is very good