Laplace transform is named in honour of the great French mathematician, Pierre Simon De Laplace (1749-1827). Like all transforms, the Laplace transform changes one signal into another according to some fixed set of rules or equations. The best way to convert differential equations into algebraic equations is the use of Laplace transformation.
Laplace transformation plays a major role in control system engineering. To analyze the control system, Laplace transforms of different functions have to be carried out. Both the properties of the Laplace transform and the inverse Laplace transformation are used in analyzing the dynamic control system. In this article, we will discuss in detail the definition of Laplace transform, its formula, properties, Laplace transform table and its applications in a detailed way.
Table of Contents:
- Definition
- Formula
- Properties
- Table
- Laplace Transform of Derivative
- Step Function
- Bilateral Laplace Transform
- Inverse Laplace Transform
- Convolution Integral
- Laplace Transform in Probability Theory
- Applications
- Examples
- Laplace Equation
- FAQs
What is the Laplace Transform?
A function is said to be a piecewise continuous function if it has a finite number of breaks and it does not blow up to infinity anywhere. Let us assume that the function f(t) is a piecewise continuous function, then f(t) is defined using the Laplace transform. The Laplace transform of a function is represented by L{f(t)} or F(s). Laplace transform helps to solve the differential equations, where it reduces the differential equation into an algebraic problem.
Laplace Transform Formula
The Laplace transform of f(t), that is denoted by L{f(t)} or F(s) is defined by the Laplace transform formula:

whenever the improper integral converges.
Standard notation: Where the notation is clear, we will use an uppercase letter to indicate the Laplace transform, e.g, L(f; s) = F(s).
The Laplace transform we defined is sometimes called the one-sided Laplace transform. There is a two-sided version where the integral goes from −∞ to ∞.
Properties of Laplace Transform
Some of the Laplace transformation properties are:
If f1 (t) ⟷ F1 (s) and [note: ⟷ implies Laplace Transform]
f2 (t) ⟷ F2 (s), then
| Linearity Property | A f1(t) + B f2(t) ⟷ A F1(s) + B F2(s) |
| Frequency Shifting Property | es0t f(t)) ⟷ F(s – s0) |
| Integration | t∫0 f(λ) dλ ⟷ 1⁄s F(s) |
| Multiplication by Time | T f(t) ⟷ (−d F(s)⁄ds) |
| Complex Shift Property | f(t) e−at ⟷ F(s + a) |
| Time Reversal Property | f (-t) ⟷ F(-s) |
| Time Scaling Property | f (t⁄a) ⟷ a F(as) |
Laplace Transform Table
The following Laplace transform table helps to solve the differential equations for different functions:
| Sl No. | f(t) | L(f(t)) = F(s) | Sl No. | f(t) | L(f(t)) = F(s) |
|---|---|---|---|---|---|
| 1 | 1 | 1/s | 11 | e(at) | 1/(s − a) |
| 2 | tn at t = 1,2,3,… | n!/s(n+1) | 12 | tp, at p>-1 | Γ(p+1)/s(p+1) |
| 3 | √(t) | √π/2s(3/2) | 13 | t(n-1/2) at n = 1,2,.. | (1.3.5…(2n-1)√π)/(2n s(n+1/2) |
| 4 | sin(at) | a/(s2+a2) | 14 | cos(at) | s/(s2+a2) |
| 5 | t sin(at) | 2as/(s2+a2)2 | 15 | t cos(at) | (s2-a2)/(s2+a2)2 |
| 6 | sin(at+b) | (s sin(b)+ a cos(b)/(s2+a2) | 16 | cos(at+b) | (s cos(b)-a sin(b)/(s2+a2) |
| 7 | sinh(at) | a/(s2-a2) | 17 | cosh(at) | s/(s2-a2) |
| 8 | e(at)sin(bt) | b/((s-a)2+b2) | 18 | e(at)cos(bt) | (s-a)/((s-a)2+b2) |
| 9 | e(ct)f(t) | F(s-c) | 19 | tnf(t) at n = 1,2,3.. | (-1)n Fn s |
| 10 | f'(t) | sF(s) – f(0) | 20 | f”(t) | s2F(s) − sf(0) − f'(0) |
Laplace Transform of Differential Equation
The Laplace transform is a well established mathematical technique for solving a differential equation. Many mathematical problems are solved using transformations. The idea is to transform the problem into another problem that is easier to solve. On the other side, the inverse transform is helpful to calculate the solution to the given problem.
For better understanding, let us solve a first-order differential equation with the help of Laplace transformation,
Consider y’- 2y = e3x and y(0) = -5. Find the value of L(y).
First step of the equation can be solved with the help of the linearity equation:
L(y’ – 2y] = L(e3x)
L(y’) – L(2y) = 1/(s-3)
(because L(eax) = 1/(s-a))
L(y’) – 2s(y) = 1/(s-3)
sL(y) – y(0) – 2L(y) = 1/(s-3)
(Using Linearity property of the Laplace transform)
L(y)(s-2) + 5 = 1/(s-3) (Use value of y(0) ie -5 (given))
L(y)(s-2) = 1/(s-3) – 5
L(y) = (-5s+16)/(s-2)(s-3) …..(1)
here (-5s+16)/(s-2)(s-3) can be written as -6/s-2 + 1/(s-3) using partial fraction method
(1) implies L(y) = -6/(s-2) + 1/(s-3)
Step Functions
The step function is often called the Heaviside function, and it is defined as follows:
The step function can take the values of 0 or 1. It is like an on and off switch. The notations that represent the Heaviside functions are uc(t) or u(t-c) or H(t-c)
Bilateral Laplace Transform
The Laplace transform can also be defined as bilateral Laplace transform. This is also known as two-sided Laplace transform, which can be performed by extending the limits of integration to be the entire real axis. Hence, the common unilateral Laplace transform becomes a special case of Bilateral Laplace transform, where the function definition is transformed is multiplied by the Heaviside step function.
The bilateral Laplace transform is defined as:
The other way to represent the bilateral Laplace transform is B{F}, instead of F.
Inverse Laplace Transform
In the inverse Laplace transform, we are provided with the transform F(s) and asked to find what function we have initially. The inverse transform of the function F(s) is given by:
f(t) = L-1{F(s)}
For example, for the two Laplace transform, say F(s) and G(s), the inverse Laplace transform is defined by:
L-1{aF(s)+bG(s)}= a L-1{F(s)}+bL-1 {G(s)}
Where a and b are constants.
In this case, we can take the inverse transform for the individual transforms, and add their constant values in their respective places, and perform the operation to get the result.
Also, check:
Convolution Integrals
If the functions f(t) and g(t) are the piecewise continuous functions on the interval [0, ∞), then the convolution integral of f(t) and g(t) is given as:
(f * g) (t) =0∫t f(t-T) g(T)dT
As, the convolution integral obey the property, (f*g)(t) = (g*) (t)
We can write, 0∫t f(t-T) g(T)dT = 0∫t f(T) g(t-T)dt
Thus, the above fact will help us to take the inverse transform of the product of transforms.
(i.e.) L(f*g) = F(s) G(s)
Laplace Transform in Probability Theory
In pure and applied probability theory, the Laplace transform is defined as the expected value. If X is the random variable with probability density function, say f, then the Laplace transform of f is given as the expectation of:
L{f}(S) = E[e-sX], which is referred to as the Laplace transform of random variable X itself.
Applications of Laplace Transform
- It is used to convert complex differential equations to a simpler form having polynomials.
- It is used to convert derivatives into multiple domain variables and then convert the polynomials back to the differential equation using Inverse Laplace transform.
- It is used in the telecommunication field to send signals to both the sides of the medium. For example, when the signals are sent through the phone then they are first converted into a time-varying wave and then superimposed on the medium.
- It is also used for many engineering tasks such as Electrical Circuit Analysis, Digital Signal Processing, System Modelling, etc.
Laplace Transform Examples
Below examples are based on some important elementary functions of Laplace transform.

Laplace Equation
Laplace’s equation, a second-order partial differential equation, is widely helpful in physics and maths. The Laplace equation states that the sum of the second-order partial derivatives of f, the unknown function, equals zero for the Cartesian coordinates. The two-dimensional Laplace equation for the function f can be written as:

The Laplace equation for three-dimensional coordinates can be represented as:

Download BYJU’S-The Learning App and get personalised videos to understand the mathematical concepts.
Frequently Asked Questions on Laplace Transform- FAQs
What is the use of Laplace Transform?
How do you calculate Laplace transform?
Step 1: Multiply the given function, i.e. f(t) by e^{-st}, where s is a complex number such that s = x + iy
Step 2; Integrate this product with respect to the time (t) by taking limits as 0 and ∞.
This process results in Laplace transformation of f(t), and is denoted by F(s).
What is the Laplace method?
What are the properties of Laplace Transform?
Linearity Property: A f_1(t) + B f_2(t) ⟷ A F_1(s) + B F_2(s)
Frequency Shifting Property: es0t f(t)) ⟷ F(s – s0)
nth Derivative Property: (d^n f(t)/ dt^n) ⟷ s^n F(s) − n∑i = 1 s^{n − i} f^{i − 1} (0^−)
Integration: t∫_0 f(λ) dλ ⟷ 1⁄s F(s)
Multiplication by Time: T f(t) ⟷ (−d F(s)⁄ds)
Complex Shift Property: f(t) e^{−at} ⟷ F(s + a)
Time Reversal Property: f (-t) ⟷ F(-s)
Time Scaling Property: f (t⁄a) ⟷ a F(as)

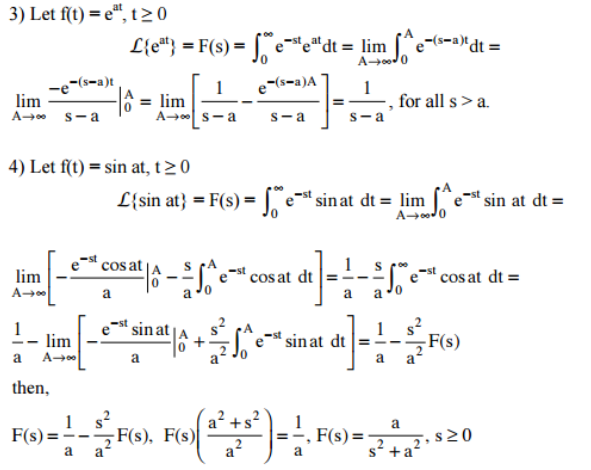
I would like to meet Divya Mam if I would get a chance