The two principal methods which are used to find the LCM (Least Common Multiple) and the HCF (Highest Common Factor) of the numbers are the Prime Factorization Method and Division Method. Both the methods are explained here with many examples. We have provided the prime factors of the given numbers, such as 24, 12, 30, 100, etc. using these methods. Here, you will learn how to find the LCM and HCF of the numbers by both the approaches. Before that, let us discuss what are LCM and HCF in detail.
Least Common Multiple (LCM)
The least or smallest common multiple of any two or more given natural numbers are termed as LCM.
For example, LCM of 10, 15 and 20 is 60.
Highest Common Factor (HCF)
The largest or greatest factor common to any two or more given natural numbers is termed as HCF of given numbers. It is also known as GCD (Greatest Common Divisor).
For example, HCF of 4, 6 and 8 is 2.
How to Find LCM and HCF?
We can find HCF and LCM of given natural numbers by two methods i.e., by prime factorization method or division method. In the prime factorization method, given numbers are written as the product of prime factors. While in the division method, given numbers are divided by the least common factor and continue still remainder is zero.
Note: Prime numbers are numbers which have only two factors i.e. one and the number itself.
LCM by Prime Factorization Method
Here, given natural numbers are written as the product of prime factors. The lowest common multiple will be the product of all prime factors with the highest degree (power).
Example 1:
Find the LCM of 20 and 12 by prime factorization method.
Solution:
Step 1: To find LCM of 20 and 12, write each number as a product of prime factors.
Step 2: Multiply all the prime factors with the highest degree.
Here we have 2 with highest power 2 and other prime factors 3 and 5. Multiply all these to get LCM.
LCM by Division Method
In this method, divide the given numbers by common prime number until the remainder is a prime number or one. LCM will be the product obtained by multiplying all divisors and remaining prime numbers.
Example 2:
Find the LCM of 24 and 15 by the division method.
Solution:
Step 1: Divide the given numbers by the least prime number.
Here, 2 is the least number which will divide 24.

Step 2: Write the quotient and the number which is not divisible by the above prime number in the second row.
In the second row, write the quotient we get after the division of 24 by 2. Since 15 is not divisible by 2, write 15 in the second row as it is.
Step 3: Divide the numbers with another least prime number.

Step 4: Continue division until the remainder is a prime number or 1.

Step 5: Multiply all the divisors and remaining prime number (if any) to obtain the LCM.
What is the LCM of 60, 84, and 108?
The LCM of 60, 84, and 108 is 3780. The LCM of 60, 84, and 108 is the least common multiple of 60, 84, and 108. The LCM of 60, 84, and 108 is found using three different methods such as prime factorization method, listing the multiples, and the division method.
Now, let us discuss all these three methods one by one to find the LCM of 60, 84, and 108.
LCM of 60, 84, and 108 by Listing Multiples
Step 1: List the multiples of 60, 84, and 108:
Multiples of 60: 60, 120, 180, 240, 300, 360, 420, 480, 540, ….
Multiples of 84: 84, 168, 252, 336, 420, 504, 588, 672, …
Multiples of 108: 108, 216, 324, 432, 540, 648, 756, 864, 972, ….
Step 2: Find the common multiples from the multiples of 60, 84, and 108:
The common multiples are 3780, 7560, …
Step 3: Determine the smallest common multiple from the multiples of 60, 84, and 108:
Thus, the least common multiple of 60, 84, and 108 is 3780.
(i.e.) LCM of 60, 84, and 108 is 3780.
LCM of 60, 84, and 108 by Prime Factorization Method
To find the LCM of 60, 84, and 108 using the prime factorization method, first write the prime factorization of 60, 84, and 108.
Therefore, the prime factorization of 60 is 22 × 31 × 51
The prime factorization of 84 is 22 × 31 × 71
The prime factorization of 108 is 22 × 33
Thus, the LCM of 60, 84, and 108 is obtained by multiplying the prime factors raised to their respective highest power.
(i.e) The least common multiple of 60, 84 and 108 = 22 × 33 × 51 × 71 = 3780.
Hence, LCM of 60, 84, and 108 is 3780.
LCM of 60, 84, and 108 by Division Method
To find the LCM of 60, 84, and 108 using the division method, divide the numbers 60, 84, and 108 by the prime factors. So, the product of the divisor gives the result of LCM of 60, 84, and 108.
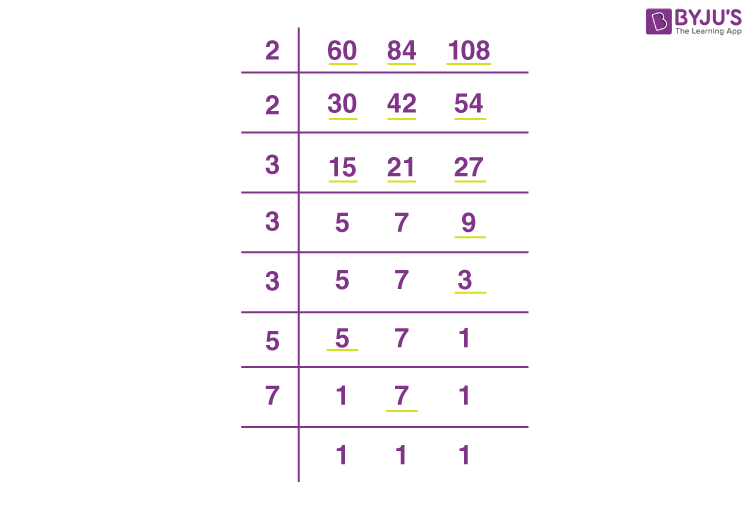
Therefore, LCM of 60, 84 and 108 = 2 × 2 × 3 × 3 × 3 × 5 × 7 = 3780.
HCF By Prime Factorization Method
Given natural numbers to be written as the product of prime factors. To obtain the highest common factor multiply all the common prime factors with the lowest degree (power).
Example 1:
Find the HCF of 20 and 12 by the prime factorization method.
Solution:
Step 1: To find HCF of 20 and 12, write each number as a product of prime factors.
20 = 2 × 2 × 5 = 22 × 5
12 = 2 × 2 × 3 = 22 × 3
Step 2: Multiply all the common prime factors with the lowest degree.
Here we have only 2 as a common prime factor with the lowest power of 2.
HCF of 20 and 12 = 22 = 4
HCF by Division Method
In this method divide the largest number by the smallest number among the given numbers until the remainder is zero. The last divisor will be the HCF of given numbers.
Example 2:
Find the HCF of 24 and 15 by the division method.
Solution:
Step 1: Divide the largest number by the smallest number.
Here, the largest number is 24 and the smaller one is 15. Divide 24 by 15

Step 2: Take divisor as new dividend and remainder as the new divisor, i.e. divide the first divisor by the first remainder.

Step 3: Proceed till the remainder is zero and the last divisor will be the HCF of the given numbers.

Therefore, HCF of 24 and 15 is 3.
Alternatively, we can divide both the numbers by the least common prime factor, still there is no more common prime factors. Multiply all divisors to get the HCF of given numbers.
Consider the above example, HCF of 24 and 15 can also be calculated using the following steps:
Step 1: Divide the given numbers by the least common prime factor.
Here, 3 is the least common prime factor of 24 and 15.

Step 2: Continue still there is no more common prime factor. Then multiply all the divisors.

Division of 24 and 15 by 3 will leave 8 and 5 as their remainders respectively. 8 and 5 do not have a common prime factor.
Hence, the HCF of 24 and 15 is 3.

Stay tuned with BYJU’S – The Learning App to learn more about the division method, prime factorization method, and much more.
Frequently Asked Questions on Prime Factorization and Division Method for LCM and HCF
What are the different methods to find the LCM of numbers?
The different methods to find the LCM of numbers are:
Prime Factorization Method
Division Method
Listing the Multiples of numbers.
What is the LCM of 60, 84, and 108?
The LCM of 60, 84, and 108 is 3780.
How to find the LCM of numbers using the prime factorization method?
Step 1: Write the prime factorization of the numbers.
Step 2: The LCM of the given number is obtained by multiplying the prime factors raised to their respective highest power.
How to find the HCF of numbers using the prime factorization method?
Step 1: Write the prime factorization of the numbers.
Step 2: Find the common prime factors.
Step 3: The HCF of the given number is the product of common prime factors with the lowest exponential power.
What is the LCM of 36 and 48?
The LCM of 36 and 48 is 144.


Hcf and lcm
https://byjus.com/maths/hcf-and-lcm/
HCF of 24,48,72
The factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
HCF of 24,48,72 = 24
24:1,2,3,4,6,8,12,24
48:1,23,4,6,8,12,16,24,48
72:1,2,3,4,6,8,9,12,18,24,36,72
Hcf of 24,48,72=24
This is a great I got it the answer this is the best app
2
4
2
4
24=24×1
48=24×2
72=24×3