Mathematics in ancient days was divided into two branches ‘Algebra’ and ‘Geometry’. Algebraic equations were not used in geometry and geometrical figures were not used in algebra. But these two branches were put together by the French mathematician Rene Descartes for the first time. He introduced the concept of the Cartesian plane or coordinate system to explain geometry and algebra together.
The number line is a straight line where the integers are placed at equal distances. All positive numbers are placed on the right-hand side of zero and all negative numbers are placed on the left-hand side of zero as shown in fig. 1.

When two number lines are placed mutually perpendicular to each other it forms coordinate axes.
Cartesian System
A Cartesian coordinate system or Coordinate system is used to locate the position of any point and that point can be plotted as an ordered pair (x, y) known as Coordinates. The horizontal number line is called X-axis and the vertical number line is called Y-axis and the point of intersection of these two axes is known as the origin and it is denoted as ‘O’.

Note:
1. The coordinate plane is also known as the 2- dimensional plane.
2. X-axis is named as XX’ and Y-axis as YY’.
Learn: Analytic geometry
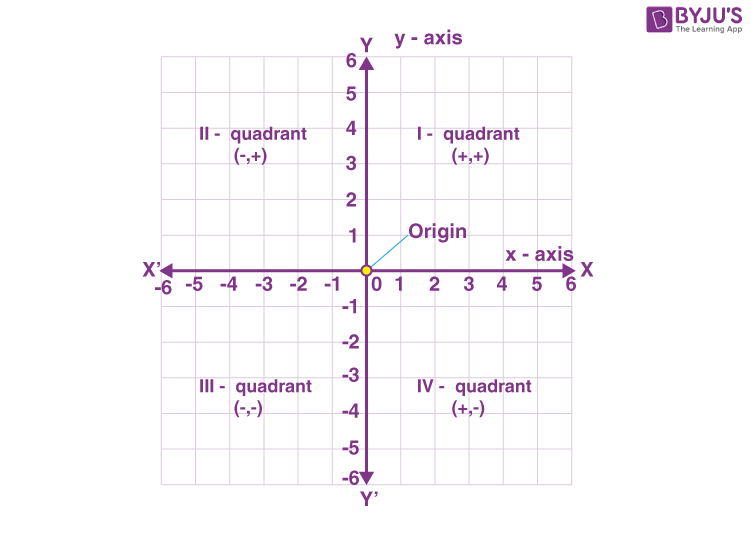
Quadrants of Coordinate System
The Coordinate axes XX’ and YY’ divides the Cartesian plane into 4 quadrants as shown in fig. 3 below:
- The region XOY is called the first quadrant
- The region X’OY is called the second quadrant
- The region X’OY’ is called the third quadrant
- The region Y’OX is called the fourth quadrant
Sign Convention
The ray OX on X-axis is taken as positive, OX’ as negative X-axis, OY on Y-axis as positive and OY’ as negative.
Accordingly, the distance measured along OX will be taken as positive and along OX’ will be negative. Similarly, the distance along OY will be taken as positive and along OY’ will be negative.
I- quadrant (+, +)
II-quadrant (-, +)
III-quadrant (-, -)
IV-quadrant (+, -)
Cartesian Co-ordinates of a point
Consider a point P in a plane.

The length of the line segment OR is called the X- coordinate or abscissa of point P and the length of the line segment OS is called the Y-coordinate or ordinate of point P.
Thus, for any given point, the abscissa and ordinate are the distance of a given point from the X-axis and Y-axis, respectively. The position of point P is given as (x, y).
Take a point on the X-axis, then clearly the distance of the point from X-axis is zero. Thus, the ordinate or Y-coordinate of every point on the X-axis is zero. Hence, the coordinate of a point on the X-axis is given as (x, 0).
Similarly, for a point on Y- axis, the distance of the point from Y-axis is zero i.e., the abscissa is zero. Hence, the coordinates of a point on the Y-axis is given by (0, y).
Note:
1. If x ≠ y, then (x, y) ≠ (y, x) and (x, y) = (y, x), only if x = y .
2. The coordinates of the origin are (0, 0).
Applications
- The coordinate plane concept is used in route maps.
- It is also used to locate the position of aircraft in the sky.
Coordinate System Types
The most commonly used coordinate systems are namely:
- Number line
- Cartesian coordinate system
- Polar coordinate system
- Cylindrical and Spherical coordinate system
As you have learned about the number line and Cartesian coordinate system in the previous section. Now, let’s have a look at the remaining types in brief.
Polar Coordinate System: In this type of coordinate system, the points in the plane will be in the form of (r, θ). Learn more on polar coordinates here.
Cylindrical and Spherical Coordinate System: These types of systems are used to represent the polar coordinates of a point in three dimensions such that the points can be written in the form of (r, θ, Φ). Learn more about the conversion of spherical coordinates into various forms here.
Practice Question
Identify the quadrant in which the following points lie.
1. (-3, 8)
2. (7, 1)
3. (4, -2)
4. (-6, -5)
To learn more maths concepts, please visit our website www.byjus.com and download BYJU’S- The Learning App.



Comments