Area Of Hexagon Formula

A polygon with six sides and six angles is termed as a hexagon. Similarly, we have Pentagon where the polygon has 5 sides; Octagon has 8 sides. Each internal angle of the hexagon has been calculated to be 120°.

In general, the sum of interior angles of a Polygon is given by:

Types of Hexagon

A hexagon can be of two types, namely

• Regular Hexagon
• Irregular Hexagon

In the case of a regular hexagon, all the sides are of equal length, and the internal angles are of the same value. The regular hexagon consists of six symmetrical lines and rotational symmetry of order of 6.

Whereas in the case of the irregular hexagon, neither the sides are equal, nor the angles are the same.

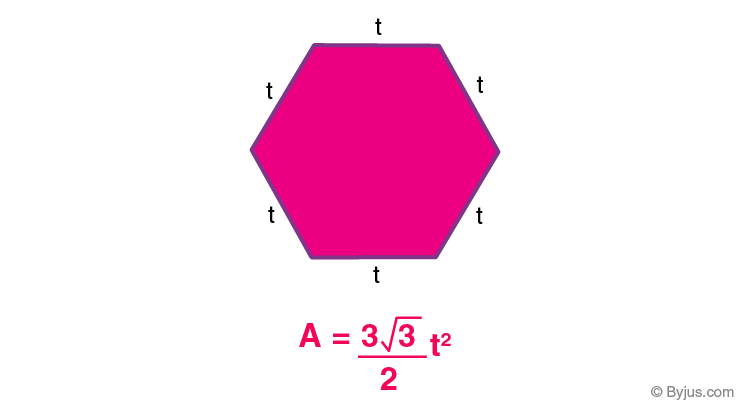
Regular Hexagon

Irregular Hexagon

Formula for the Area of a Hexagon

Area of the hexagon is the space confined within the sides of the polygon.

The area of Hexagon is given by

Where “x” denotes the sides of the hexagon.

There is one more formula that could be used to calculate the area of regular Hexagon:

Where “t” is the length of each side of the hexagon and “d” is the height of the hexagon when it is made to lie on one of the bases of it.

Similarly, to find the area of the polygons- like the area of a regular pentagon, area of the octagon, go through the below formula.

Area of Pentagon:

Area of Regular Pentagon= (5/2) × s × a

Where ‘a’ denotes the length apothem length and “s” denotes the side length of a pentagon.

Area of Octagon:

Where ‘a’ denotes the length of each side of the octagon.

Area of a Hexagon Problems

Question 1: 
Find the area of a regular hexagon whose side is 4 cm?

Solution:
Given
s = 4 cm

A = 41.57 cm. sq.

This is all about the area of a hexagon. To know more about the other characteristics and attributes of polygons such as hexagon, pentagon, octagon and other geometrical figures, please visit our site or download BYJU’S – The Learning App.