Area of a polygon is the region occupied by a polygon. Polygons can be regular and irregular. The basic polygons which are used in geometry are triangle, square, rectangle, pentagon, hexagon, etc. All these polygons have their own area. For the regular polygons, it is easy to find the area for them, since the dimensions are definite and known to us. For example, area of square can be easily determined if we know the length of its one side since all its sides are equal.
You are already acquainted with the term area. It is defined as the region occupied inside the boundary of a flat object or figure. The measurement is done in square units with the standard unit being square meters (m2). For the computation of area, there are pre-defined formulas for Squares, Rectangles, Circle, Triangles, Trapeziums, etc. However, for an irregular polygon, the area is calculated by viewing it as a combination of 2 or more regular polygons. In this article, you will learn about the area of a polygon in general.
Table of contents:
Area of Polygon Definition
The area of any given polygon whether it a triangle, square, quadrilateral, rectangle, parallelogram or rhombus, hexagon or pentagon, is defined as the region occupied by it in a two-dimensional plane.
The areas or formulas for areas of different types of polygon depends on their shapes. Suppose, to find the area of the triangle, we have to know the length of its base and height.
Let us learn here to find the area of all the polygons.
How to Find Area of Polygon with n-sides?
For finding the area of a polygon which is not regular or its formula is not defined, we split the figure into triangles, squares, trapezium, etc. The purpose is to visualize the given geometry as a combination of geometries for which we know how to calculate the area. We then calculate the area for each of the part and then add them up to obtain the area of the polygon.
For example, consider the polygon shown below:

This polygon can be divided into a combination of triangles and trapezium.


We can calculate the area considering any of the above divisions. In the first figure, we can sum up the area of the triangle as well as the trapezium to obtain the area of the polygon. In the second one, we add the areas of the three triangles to get the area of a polygon. In either case, the result is the same.
Area of Polygon Formulas
Let us discuss here some formulas for different types of polygons. Here we are considering the formulas for a regular polygon.
| Name of the Polygon | Area Formula |
| Triangle | 1/2 × base × height |
| Square | side2 |
| Rectangle | length × width |
| Pentagon | 5/2 × side length × distance from the center of sides to the center of pentagon |
| Rhombus | 1/2 × product of diagonals |
| Hexagon | (3√3)/2 × distance from center of sides to the center of hexagon |
Also, read:
Solved Example
Example: Find the area of polygon ABCDEFG. The measurements (in cm) are shown in the figure.
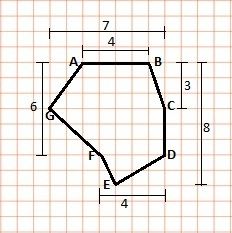
Solution: The polygon can be split into two trapeziums and a triangle.
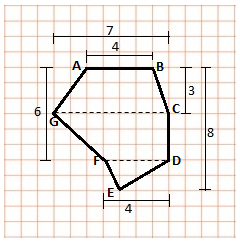
So, the area of polygon ABCDEFG is given by the sum of the area of trapezium ABCG and CDFG and the area of triangle DEF.
Height of trapezium ABCG = 3 cm
Height of trapezium CDFG = (6 – 3) = 3 cm
Height of triangle DEF = (8 – 6) = 2 cm
Area of trapezium ABCG = (sum of parallel sides) × height/2 = (4 + 7)×3/2 = 33/2 = 16.5 cm2
Area of trapezium CDFG = (7 + 4) ×3/2 = 33/2 = 16.5 cm2
Area of triangle DEF = (base ×height)/2 = (4 × 2)/2 = 8/2 = 4 cm2
So, area of polygon ABCDEFG = area of ABCG + area of CDFG + area of DEF
= 16.5 + 16.5 + 4 = 37 cm2

Comments